No post de hoje, como parte do que ensinamos no nosso curso R para o Mercado Financeiro, continuaremos a mostrar como podemos realizar cálculos úteis para avaliações de investimentos. No post passado, mostramos como podemos realizar cálculos dos retorno de ativos individualmente, porém, no mundo real, nem sempre iremos investir nosso dinheiro todo em um único ativo. Por isso, deve-se ser necessário o entendimento de como podemos calcular o retorno de um portfólio de ativos.
Sem muito suspense, o retorno de um portfólio é simplesmente a soma do retorno ponderado pelo peso dos ativos baseado no total de dinheiro investido. De outra forma, podemos definir através de uma equação:
(1)
onde é o retorno do portfólio,
o dinheiro investido no ativo 1,
o dinheiro investido no ativo 2,
o retorno do ativo 1 e
o retorno do ativo 2.
Nesse caso, utilizamos apenas dois ativos como exemplo na equação, mas o mesmo funciona para caso houver mais ativos no portfólio, sendo necessário apenas expandir a equação.
Mas, como podemos realizar isso no R? É bem simples!
Primeiro iremos carregar os pacotes necessários.
library(quantmod) library(Quandl) library(PerformanceAnalytics) library(tidyverse) library(timetk)
Em seguida, podemos seguir para o nosso código.
# Define os ativos que irão ser coletados
tickers <- c("PETR4.SA", "ITUB4.SA", "ABEV3.SA", "JBSS3.SA")
# Define a data de início da coleta
start <- "2016-12-01"
# Realiza a coleta dos preços diários
prices <- getSymbols(tickers,
auto.assign = TRUE,
warnings = FALSE,
from = start,
src = "yahoo") %>%
map(~Cl(get(.))) %>%
reduce(merge) %>%
`colnames<-`(tickers)
# Transfroma os preços diários em mensais
prices_monthly <- to.monthly(prices,
indexAt = "lastof",
OHLC = FALSE)
# Calcula os retornos mensais
asset_returns <- Return.calculate(prices_monthly,
method = "log") %>%
na.omit()
Veja que até aqui somente tratamos de calcular os retornos individuais dos nossos ativos. Agora, será o momento que devemos realizar o cálculo do retorno do portfólio. Para isso, iremos construir quatro portfólio diferentes, de forma que possamos validar qual a melhor estratégia que podemos utilizar.
Iremos fazer da seguinte forma, através de 4 ativos, com pesos escolhidos aleatoriamente, definimos: PETR4 com peso de 50%; ITUB4 com peso de 27%; ABEV3 com peso de 13% e JBSS3 com peso de 10%.
# Define os pesos dos respectivos ativos
w <- c(0.50, 0.27, 0.13, 0.10)
# Calcula o retorno do portfolio baseado no peso de cada ativo
portfolio_return <- Return.portfolio(asset_returns,
weights = w) %>%
`colnames<-`("port_returns")
Através da função Return.portfolio(), calculamos o retorno do portfolio com os retornos individuais e com os pesos escolhidos.
No segundo portfólio, iremos utilizar as mesmas métricas, porém, deixaremos que a função faça um rebalanceamento.
# Calcula o retorno do portfolio baseado no peso de cada ativo com rebalanceamento
portfolio_return_reb <- Return.portfolio(asset_returns,
weights = w,
rebalance_on = "quarters") %>%
`colnames<-`("port_return_reb")
No terceiro portfólio, iremos construir o que a literatura conhece como equally weighted portfolio, no qual estabelece que todos os ativos possuem o mesmo peso.
# Calcula o Equally Weighted Portfolio
portfolio_return_ew <- Return.portfolio(asset_returns) %>%
`colnames<-`("ewp")
E por fim, no quarto portfólio, criamos novamente o equally weighted portfolio, porém, com rebalanceamento.
# Calcula o Equally Weighted Portfolio com rebalanceamento
portfolio_return_ew_reb <- Return.portfolio(asset_returns,
rebalance_on = "quarters") %>%
`colnames<-`("ewp_reb")
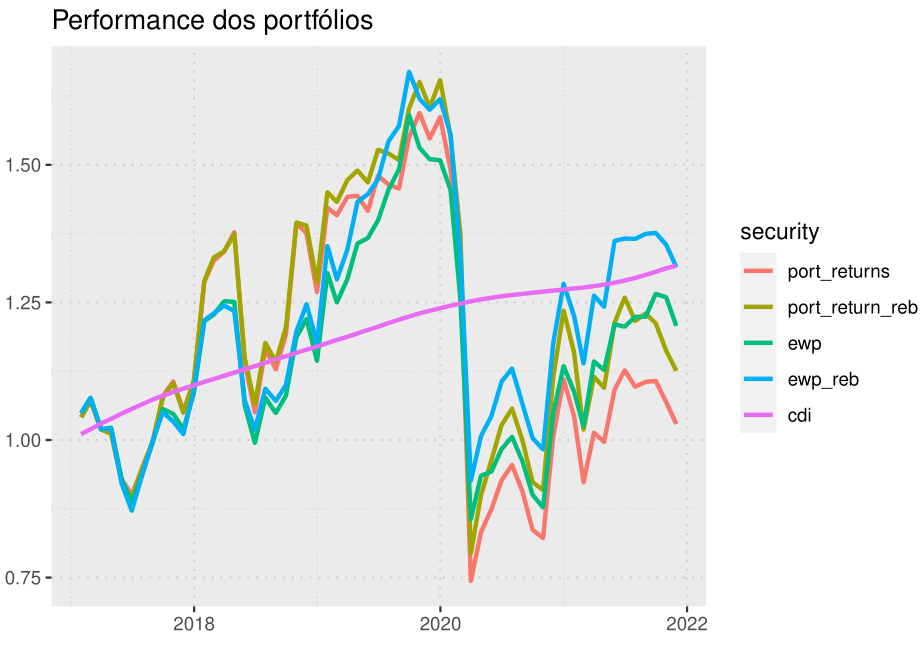
Podemos então visualizar a performance do nosso portfólio através do retorno acumulado, comparando-os entre si, e também com CDI.
Parece que teremos que revisar nossas estratégias.
________________________
(*) Para entender mais sobre Mercado Financeiro e aprender como realizar a coleta, tratamento e visualização de dados financeiros, confira nosso curso de R para o Mercado Financeiro.
________________________