Quando se fala em estudos financeiros, bem como formas de analisar investimentos, o retorno é a principal medida utiliza para se realizar cálculos e comparações de ativos ao longo do tempo. Existe inúmeros motivos para isso, tanto estatísticos, quanto pela própria teoria e prática de finanças. Hoje, iremos ensinar como transformar os preços de ações em retornos através do R.
Para quem não sabe, o retorno simples de um ativo é dado pela diferença de seu valor no tempo e
dividido pelo valor no tempo
, sendo
.
Outro método de cálculo se dá através do Retorno Contínuo: .
library(tidyverse) library(PerformanceAnalytics) library(quantmod)
Para realizar esse cálculo através do R, vamos primeiro coletar o dados de forma reprodutível, utilizando o pacote {quantmod}. Iremos coletar os preços de fechamento de três empresas aleatórias e tratá-las de forma que estejam em um data frame da classe xts.
tickers = c('PETR4.SA', 'ABEV3.SA', 'MGLU3.SA')
prices = getSymbols(tickers, src='yahoo',
from='2021-01-01',
warning=FALSE) %>%
map(~Ad(get(.))) %>%
reduce(merge) %>%
`colnames<-` (tickers)
Após coletar e tratar os dados, podemos calcular os retornos através da função do pacote {PerformanceAnalytics}, chamada Return.calculate(). É necessário somente o data frame da classe xts do preço dos ativos e especificar o método de calculo dos retornos. No caso, utilizaremos "discrete" para o retorno simples e "log" para o retorno contínuo.
# Calcula os retornos discretos
returns_discrete <- Return.calculate(prices,
method = "discrete") %>%
na.omit()
# Calcula os retornos contínuos
returns_log <- Return.calculate(prices,
method = "log") %>%
na.omit()
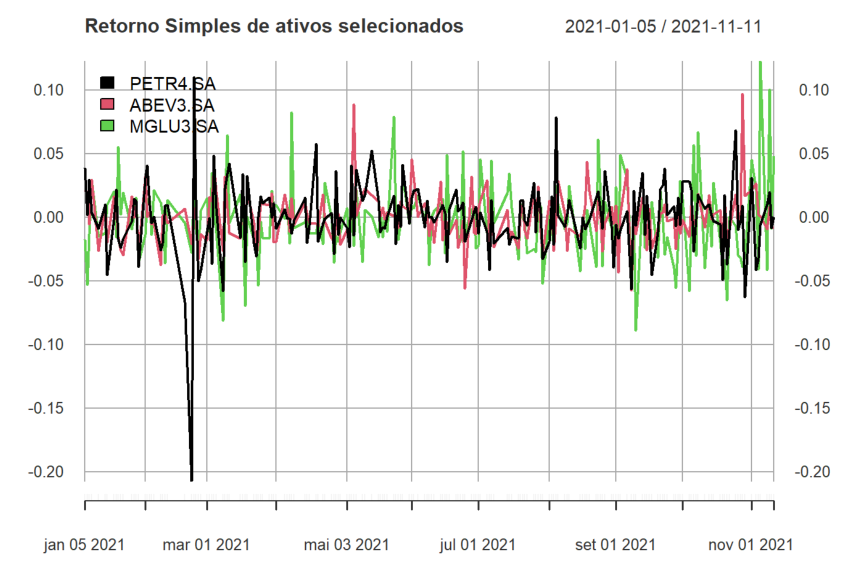
Podemos plotar os retornos dos nossos ativos.
plot(returns_discrete,
legend.loc = "topleft",
main = "Retorno Simples de ativos selecionados")
Podemos também visualizar o retorno cumulativo ao longo do tempo.
chart.CumReturns(returns_log,
legend.loc = "topleft",
main = "Retorno Acumulado de ativos selecionados")
________________________
(*) Para entender mais sobre Mercado Financeiro e aprender como realizar a coleta, tratamento e visualização de dados financeiros, confira nosso curso de R para o Mercado Financeiro.
________________________