É comum em nossas vidas construirmos raciocínios lógicos, a partir de acontecimentos do passado, de que tal variável afetou outra. Muitas vezes, lidamos com diversas teorias que demonstram esses raciocínios de forma cuidadosa de acordo com uma história de acontecimentos e de relações entre as variáveis. Mas, e se tivesse uma forma de conseguir estimar, numericamente o efeito dessas relações? Saber se há significância, ou até mesmo, conseguir a partir do efeito numérico prever um resultado? Tudo isso é possível a partir de uma regressão linear, como mostraremos no post de hoje utilizando o R e o Python.
Regressão Linear
O objetivo principal da Regressão Linear, é a partir de uma equação matemática, definir o efeito de uma ou mais variável independente em uma variável dependente. O nome linear vem justamente da forma de sua equação, no qual define que esse efeito de relacionamentos é uma função linear dos seus parâmetros. Definimos a equação da seguinte forma:
Nesta equação definimos uma Regressão Linear Simples, pois há somente uma variável independente x, que afeta a variável dependente Y. Ou seja, através desta equação, definimos o efeito de x em Y. O a é uma constante, que mensura o valor da estimativa caso x seja zero. O b (beta) é o parâmetro (ou coeficiente) que mensura a magnitude de uma variação de x em Y. O erro (também conhecido como resíduo) é simplesmente a diferente entre o valor observado de y com o valor estimado pela equação construída de Y, contendo basicamente as variáveis omitidas do modelo.
Para que não possamos incorrer de muitos erros na Regressão, de forma contenha muitas variáveis omitidas e o valor predito não seja cheio de erros, podemos aumentar o número de variáveis independente de forma que diminua o valor do erro. Sendo assim, construímos uma Regressão Linear Múltipla, denotada pela equação, um pouco mais formal da seguinte forma:
Para estimar o valor de , o método mais comum é através do Mínimo Quadrados Ordinários, que através do conjunto de dados, minimiza o erro, através soma dos quadrados das diferenças entre o valor estimado e os dados observados. Esse tipo de método é mais comum, devido ao fato de que seus pressuposto são menos rígidos. A equação para Beta segue como:
Feito todas as considerações iniciais, podemos partir para um exemplo real no R e Python para exemplificar melhor o conceito de Regressão.
Regressão Linear no R
Criar uma Regressão Linear no R é algo extremamente simples. O que precisamos ter em mãos são os dados da variável dependente e da(s) variável(is) independente(s) e utilizar a função lm() com a fórmula da Regressão como argumento.
Regressão Linear no R: modelo simples de precificação de ativos
Um exemplo para mostrar o efeito de x sobre y ocorre no contexto de finanças, no qual podemos estimar o retorno de um ativo com base no retorno do mercado. Este é um modelo básico que se utiliza a Regressão Linear Simples e é útil para aqueles que queiram entender melhor sobre o efeito prático das relações entre duas variáveis.
Não iremos discorrer muito sobre a importação e transformação de dados. Essa parte ensinamos por completo no nosso curso de R para o Mercado Financeiro.
Importamos os preços de um ativo no R, bem como os pontos do Ibovespa no mesmo período. Transformamos ambos em forma de retorno diário (isto é, a variação do preço de um dia para o outro). O que queremos saber: o quanto a variação do retorno do Ibovespa, tido aqui como o Retorno do Mercado, afeta o Retorno do Ativo?
Após obter nossos dados, podemos utilizar a função lm() para calcular a regressão. Veja que usamos o simbolo ~, significando que o lado esquerdo (PETR4) é em função da direita (^BVSP). Com a função summary(), sumarizamos os resultados da regressão, obtendo os coeficientes, a significância e o R².
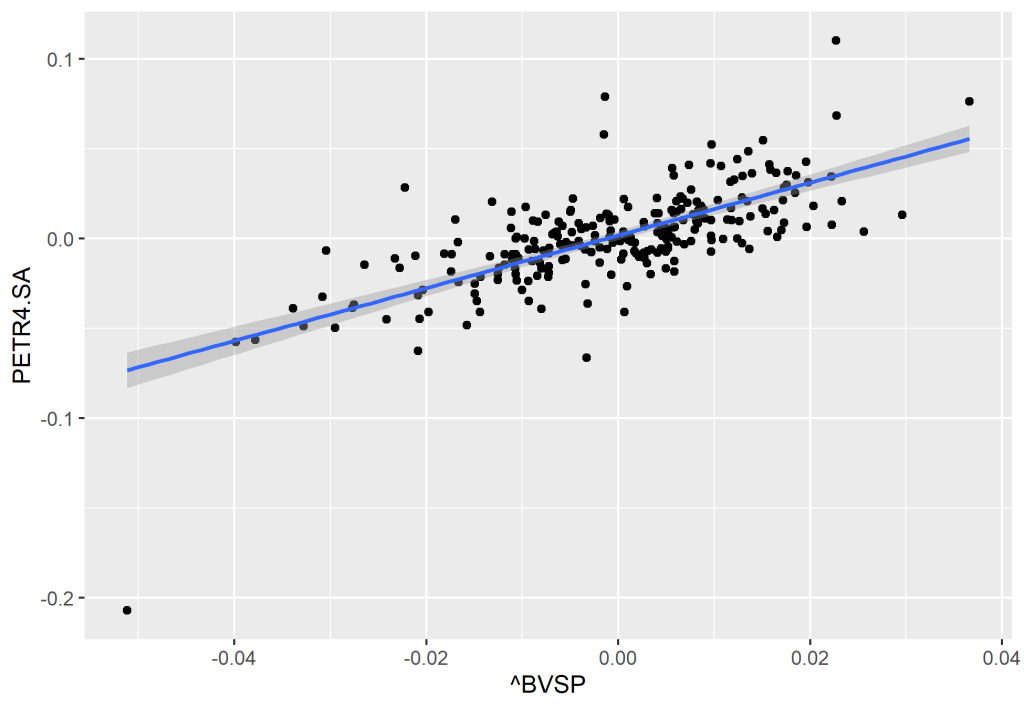
A grosso modo, a leitura dos resultados fica como: A estimativa da constante (intercepto) é igual a 0.001769, a estimativa do coeficiente beta dos retornos da Ibovespa é igual a 1.467227. O intercepto possui um p-valor de 0.16, ou seja, não é significante. Já o coeficiente dos retornos do Ibovespa possui um valor de 2e-16, ou seja, é significante. Medido pelo R², a variabilidade do Ibovespa explica 49,13% da PETR4. Por óbvio, não devemos tirar nenhuma relação de causalidade aqui, apenas de relacionamento entre as variáveis.
Um ponto interessante da Regressão Linear é também poder visualizar a relação de duas variáveis. Utilizando um gráfico de dispersão, é possível ver o relacionamento entre as observações das variáveis, também é possível criar uma Reta de Regressão, na qual realiza o ajuste entre a dispersão dos dados.
No R, criamos um gráfico de dispersão com reta de regressão através do pacote {ggplot2}.
 Regressão Linear no Python
Regressão Linear no Python
No Python, seguiremos o processo igual, retirando os mesmo dados da internet e transformando-os em retornos. Para criar a regressão, utilizaremos a função ols() da biblioteca statsmodels e de sey API formula.api.
No código abaixo seguiremos passos iguais que fizemos no R, importando os preços dos ativos e calculando os retornos diários, além de outros tratamentos.
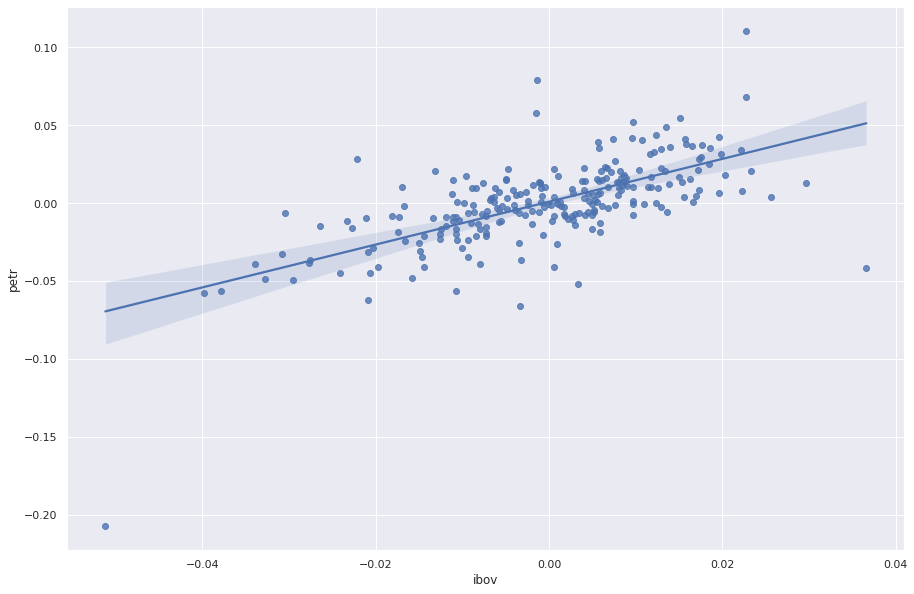
Por fim, criamos a regressão utilizando a smf.ols com a respectiva formula como argumento. Visualizamos os resultados com fit() e summary(). Apesar de ligeiramente diferente do output do R, os principais resultados estão contidos. Há também uma ligeira diferença dos resultado também, devido ao arredondamento dos dados, porém, bem próximos.
Também é possível criar facilmente um gráfico de dispersão com um Reta de Regressão no Python, para isso, utilizamos a biblioteca {seaborn}.
 Quer saber mais sobre R e Python?
Quer saber mais sobre R e Python?
Veja nossos cursos de aplicados de R e Python para Economistas. Também oferecemos cursos aplicado ao mercado financeiro através do nosso cursos R para o Mercado Financeiro