Motivação
Na vida real dificilmente encontramos em séries temporais (econômicas) características desejáveis como estacionariedade e linearidade. Modelos econométricos bastante conhecidos como o ARIMA podem contornar o primeiro problema ao diferenciar a série, mas falham em capturar não linearidades. Dessa forma, modelos não lineares precisam ser empregados e um candidato natural é o modelo de redes neurais.
A arquitetura de uma rede neural simples
As redes neurais são métodos de previsão baseados em modelos matemáticos simples do cérebro, capazes de realizar aprendizado de máquina. Elas permitem relacionamentos não lineares complexos entre a variável de interesse e suas regressoras.
Uma rede neural pode ser pensada como uma rede de "neurônios" organizados em camadas. Os regressores (ou inputs) formam a camada inferior e as previsões (ou outputs) formam a camada superior. Também pode haver camadas intermediárias contendo "neurônios ocultos". As redes neurais mais simples não contêm camadas ocultas e são equivalentes a regressões lineares.
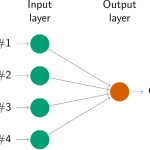
O diagrama a seguir mostra a versão de rede neural de uma regressão linear com quatro regressores. Os coeficientes associados a esses regressores são chamados de "pesos". As previsões são obtidas por uma combinação linear dos inputs. Os pesos são selecionados na estrutura da rede neural usando um "algoritmo de aprendizado" cujo objetivo é minimizar uma "função de custo" - como o EQM - e é comumente chamado de "algoritmo de aprendizagem por retropropagação do erro".
Fonte: Hyndman and Athanasopoulos (2021)
Uma rede neural com camada oculta
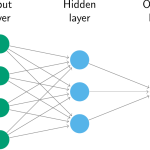
Uma vez que adicionamos uma camada intermediária com neurônios ocultos, a rede neural se torna não linear. Um exemplo simples é mostrado no diagrama a seguir.
Fonte: Hyndman and Athanasopoulos (2021)
Isso é conhecido como uma rede multilayer feed-forward network, onde cada camada de nós recebe entradas das camadas anteriores. As saídas dos nós em uma camada são entradas para a próxima camada. As entradas para cada nó são combinadas usando uma combinação linear ponderada. O resultado é então modificado por uma função não linear (como uma função sigmoide) antes de ser gerado. Isso tende a reduzir o efeito de valores extremos de entrada, tornando a rede um pouco robusta a outliers.
O número de camadas ocultas e o número de nós em cada camada oculta devem ser especificados.
Autoregressão de rede neural (NNAR)
Em se tratando de séries temporais, valores defasados da série podem ser usados como entradas em uma rede neural, assim como usamos valores defasados em um modelo autorregressivo (AR).
Tomando como exemplo uma rede neural com uma camada oculta, usamos a notação NNAR(p, k) para indicar que existem p entradas defasadas e k nós na camada oculta. Por exemplo, um modelo NNAR(9, 3) é uma rede neural com as últimas nove observações usadas como entradas para prever a saída yt e possui 3 neurônios na camada oculta.
Da mesma forma, podemos representar e usar o NNAR para séries sazonais, como é característico em dados que buscam representar o mercado de trabalho de uma economia, por exemplo a taxa de desocupação.
O modelo tem como vantagem a menor complexidade e maior interpretabilidade em relação a um modelo com múltiplas camadas ocultas. Para saber mais veja Hyndman e Athanasopoulos (2021) e Faraway e Chatfeld (1998).
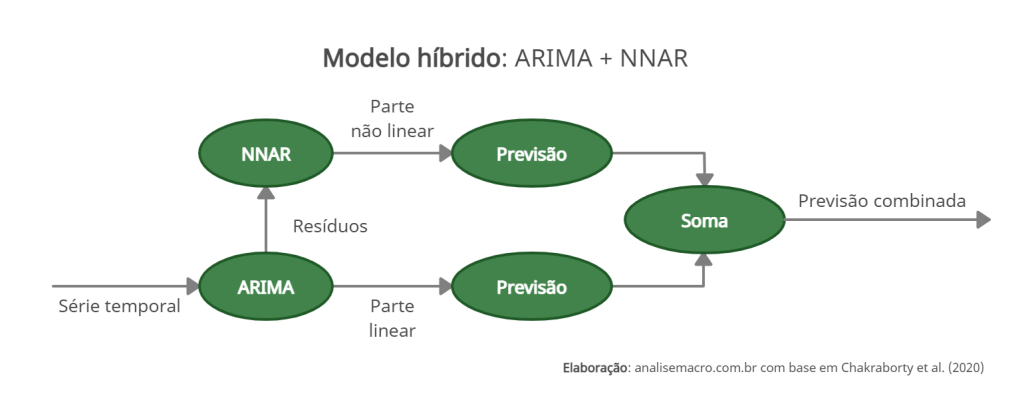
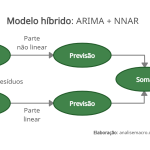
Modelo híbrido: ARIMA + NNAR
De forma a explorar as características lineares e não lineares da série temporal da taxa de desocupação brasileira (PNADC-M/IBGE), e seguindo Chakraborty et al. (2020), propomos um algoritmo em dois estágios que constrói um modelo híbrido de previsão, assumindo que os modelos podem captar as características separadamente e então suas previsões podem ser combinadas. O diagrama abaixo sintetiza a abordagem:
Exemplo com a taxa de desocupação
Para testar empiricamente a abordagem proposta, implementamos o algoritmo usando o pacote {fable} (veja um tutorial aqui) no R e comparamos os resultados com as previsões de mercado disponibilizadas no sistema de expectativas (Focus) do Banco Central do Brasil (BCB). Há poucos dados de expectativas de mercado para a taxa de desocupação (PNADC-M), dado que a coleta dessa informação se iniciou em 2021 pelo BCB, limitando a comparação. O objetivo é verificar se o modelo híbrido ARIMA+NNAR supera em termos de acurácia as previsões de mercado.
O exercício foi implementado usando validação cruzada e considerando uma janela amostral crescente, partindo de 112 observações iniciais e adicionando 1 observação a cada iteração. As previsões foram geradas no horizonte de 6 meses (pseudo) fora da amostra a partir de cada sub amostra de validação cruzada, possibilitando o cálculo de métricas de acurácia por horizonte preditivo (1, 2, ..., 6 meses).
Os dados do Focus foram tratados de modo a filtrar a expectativa mais recente disponível para uma dada data de referência. O IBGE divulga a taxa de desocupação mensalmente com um atraso de ≈ 1 mês, dessa forma consideramos como horizonte preditivo, de forma a comparar as previsões, a diferença em meses da expectativa registrada no Focus na data j em relação a data de referência t deste indicador. Dado a assincronia/atraso de divulgação da maioria dos dados econômicos em relação as suas datas de referência, as expectativas registradas no Focus após a data de referência são tomadas como expectativas futuras (o BCB aceita expectativas para o indicador até a data anterior a sua divulgação).
Resultados
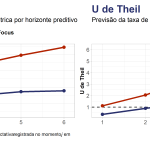
O gráfico abaixo compara, por horizonte de previsão, o modelo híbrido ARIMA+NNAR e as previsões de mercado do Focus através da métrica de erro RMSE e pelo U de Theil. Por ambas as métricas o modelo proposto apresenta resultados melhores em relação ao benchmark de mercado, superando também as previsões de um modelo de passeio aleatório nos horizontes de 1 a 2 meses.
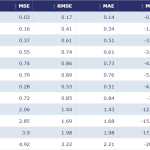
A tabela abaixo apresenta outras métricas de acurácia calculadas:
Comentários
Os resultados apresentados estão em linha com o encontrado por Chakraborty et al. (2020) para diversas outras economias que apresentam taxas de desemprego com características semelhantes à série brasileira, como Canada, Alemanha, Japão, Holanda, Nova Zelândia, Suécia e Suíça.
Apesar disso, melhorias e aprofundamentos da abordagem podem ser objeto de futura investigação. Como exemplo, destacamos que a abordagem é intensiva computacionalmente, havendo contribuições tanto do algoritmo do ARIMA quanto do NNAR para a morosidade dos procedimentos de estimação e previsão.
Códigos de R para replicação estão disponíveis para membros do Clube AM da Análise Macro.
Referências
Chakraborty, T., Chakraborty, A. K., Biswas, M., Banerjee, S., & Bhattacharya, S. (2020). Unemployment Rate Forecasting: A Hybrid Approach. Computational Economics. doi:10.1007/s10614-020-10040-2
Faraway, J., & Chatfeld, C. (1998). Time series forecasting with neural networks: A comparative study using the air line data. Journal of the Royal Statistical Society: Series C (Applied Statistics), 47(2), 231–250.
Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2022-04-01.