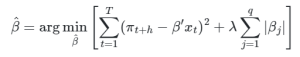Este exercício é um resumo de uma parte do curso de modelos preditivos da Análise Macro, onde o objetivo é desenvolver modelos para prever a inflação brasileira medida pelo IPCA, usando técnicas de Machine Learning e uma abordagem automatizada.
Por que usar Machine Learning?
Com vistas a obter melhor acurácia preditiva, Garcia et al. (2017) e Medeiros et al. (2019) mostraram que há benefícios no uso de conjuntos maiores de dados, disponíveis de forma muito rica e proliferada atualmente. Em especial, o uso conjunto de grandes bases de dados com modelos de Machine Learning costuma apresentar melhores resultados de performance em relação a modelos mais clássicos como AR, Random Walk e, até mesmo, curva de Phillips para previsão da inflação. Neste exercício exploraremos estas possibilidades.
Estratégia de previsão
Consideramos uma abordagem de previsão dinâmica onde a inflação ℎ períodos à frente, πt+ℎ, é modelada em função de um conjunto de preditores medidos no tempo t, tal como:
onde G(xt) é um mapeamento de um conjunto de preditores q que pode ser de um único modelo ou de uma combinação (ensemble) de modelos; xt = (x1t, …, xqt)′ é um q-vetor que pode incluir preditores fracamente exógenos, valores defasados dos preditores e de πt e dummies sazonais; e ut é um erro aleatório de média zero.
Nossa estratégia é prever o IPCA todo dia 15 de cada mês, quando o índice do mês anterior já foi divulgado pelo IBGE. Assim, todos as variáveis utilizadas em modelos são as que estiverem disponíveis até o dia 15. No caso de dados do Focus, como são de frequência irregular e divulgados apenas em dias úteis, escolhemos sempre as últimas estatísticas disponíveis até o dia 15 de cada mês, optando por usar a mediana das expectativas para cada um dos próximos 12 meses.
Quais variáveis serão utilizadas?
Buscou-se utilizar dados que representassem diferentes áreas da economia, como monetária, fiscal, financeiro, mercado de trabalho e produção. Dessa forma, foi selecionado um conjunto de 33 variáveis exógenas — além do próprio IPCA —, para criar uma base maior e expandida com 1 até 4 defasagens, totalizando assim, após seleções descritas adiante, um conjunto com 159 variáveis potencialmente preditoras, incluindo dummies sazonais.
Descrevemos alguns metadados das variáveis utilizadas a seguir, que foram selecionadas com base em trabalhos que buscaram prever a inflação, como Baybuza (2018), Mandalinci (2017) e, principalmente para o Brasil, os já citados Garcia et al. (2017) e Medeiros et al. (2019).
| Variável | Unidade de Medida | Fonte |
|---|---|---|
| Índice Nacional de Preços ao Consumidor Amplo (IPCA) | % a.m. | IBGE |
| Taxa de câmbio - Livre - Venda - Média mensal | R$/US$ | BCB |
| Interesse por “seguro desemprego” - Brasil | Índice | Google Trends |
| Custo médio m² - Construção Civil - Variação % em 12 meses | % | IBGE |
| Taxa de juros pré fixada - Estrutura a termo - LTN - 12 meses - Anbima | % a.a. | IPEADATA |
| PIB mensal - Valores correntes | R$ milhões | BCB |
| Índice geral de preços - Mercado (IGP-M) - FGV | % a.m. | BCB |
| Índice geral de preços - Disponibilidade interna (IGP-DI) - FGV | % a.m. | BCB |
| Meios de pagamento - M1 - Média dos dias úteis do mês | R$ mil | BCB |
| Meios de pagamento amplos - M2 - Saldo em final de período | R$ mil | BCB |
| Meios de pagamento amplos - M3 - Saldo em final de período | R$ mil | BCB |
| Meios de pagamento amplos - M4 - Saldo em final de período | R$ mil | BCB |
| Produção Industrial de Bens de Consumo - PIM-PF | % a.m. | IBGE |
| Estoque de empregos formais - Total - Encadeamento do antigo e novo CAGED | Pessoa | BCB |
| Balança comercial - Balanço de Pagamentos BPM6 - Mensal - Saldo | US$ milhões | BCB |
| Imposto sobre a renda (IR) - Total - Receita bruta - ME | R$ milhões | IPEADATA |
| Ibovespa - Índice de ações - Fechamento - Anbima | % a.m. | IPEADATA |
| Índice de volume de vendas no comércio varejista ampliado - PMC | % a.a. | IBGE |
| Vendas de veículos pelas concessionárias - Automóveis - Fenabrave | Automóvel | BCB |
| Dívida Líquida do Setor Público - Total - Setor público consolidado | % PIB | BCB |
| Consumo de energia elétrica - Comercial - Quantidade - Eletrobras | GWh | IPEADATA |
| Preço - petróleo bruto - Brent - FOB - Energy Information Administration (EIA) | US$/barril | IPEADATA |
| Expectativas de mercado mensais de inflação - IPCA - Focus/BCB | % | Focus/BCB |
Modelos
Como utilizaremos um total de 159 variáveis possivelmente preditoras e, em em exercícios de previsão, costuma-se dividir a amostra em conjuntos de dados de treino e teste para comparar modelos, ou ainda utilizar validação cruzada, podemos incorrer no problema de alta dimensionalidade, onde há mais variáveis do que observações amostrais. Essa é uma questão que traz implicações estatísticas bastante relevantes, como baixa generalização dos modelos (Friedman et al., 2001), o que implica que precisamos utilizar métodos que sejam específicos para tratar esse problema de dimensionalidade.
- Complete Subset Regression
- Bagging
- LASSO
Além destes modelos, criaremos uma combinação (ensemble) usando a média das previsões dos modelos. A motivação é de que há muito se sabe, na literatura de previsão, que quando combinamos diferentes modelos temos resultados, em média, melhores do que os resultados individuais de suas previsões. Formas mais robustas de combinar as previsões também podem ser aplicadas, conforme Kolassa (2011). A seguir descrevemos brevemente cada modelo.
Complete Subset Regression (CSR)
Esse é um método relativamente novo e simples, apresentado por Elliott et al. (2013), sendo bastante interessante para problemas com alta dimensionalidade. Nele são estimadas todas as regressões possíveis de combinações entre as variáveis preditoras, o que auxilia no controle do problema da multicolinearidade. Entretanto, estimar todas as combinações possíveis em 159 variáveis é intensivo computacionalmente, de forma que seguimos o procedimento adotado por Garcia et al. (2017), em que há um procedimento de “pré teste” com cada uma das variáveis estimadas em uma regressão simples contra o IPCA. Assim, são selecionadas as 20 variáveis com melhores valores na estatística t e com elas são estimadas todas as combinações possíveis de regressões com 15 parâmetros, totalizando
factorial(20) / ((factorial(20 - 15) * factorial(15))) = 15504
regressões. Tomando a média das previsões dessas regressões, temos a previsão do modelo.
Bagging
O Bagging é uma técnica que visa diminuir a instabilidade de modelos (Friedman et al., 2001). A ideia é combinar previsões de vários modelos instáveis estimados para diferentes subamostras de bootstrap, que é um processo de reamostragem aleatória com substituição. Normalmente, há muito mais a ganhar com combinações de modelos se forem muito diferentes. As etapas de Bagging pode ser descritas conforme abaixo:
- Para cada amostra de bootstrap, rode uma regressão MQO com todas as variáveis candidatas e selecione aquelas com uma estatística t absoluta acima de um certo limite c;
- Estime uma nova regressão apenas com as variáveis selecionadas na etapa anterior;
- Os coeficientes da segunda regressão são então usados para calcular as previsões na amostra real;
- Repita as três primeiras etapas para B amostras de bootstrap e calcule a previsão final como a média das B previsões.
O principal efeito desse modelo é evitar que ruídos deixem de fora variáveis importantes para a previsão, melhorando capacidade do modelo de generalização (bom desempenho em dados futuros). Optamos por escolher 500 replicações de bootstrap, mas esse valor é arbitrário.
LASSO
LASSO (Least Absolute Shrinkage and Selection Operator) é um método desenvolvido por Tibshirani (1996) que tem como objetivo reduzir o número de parâmetros, principalmente em casos de multicolineariedade. Para tal, é adicionado à minimização dos mínimos quadrados (MQO) uma penalização de magnitude λ aos parametros de variáveis irrelevantes, qué determinado por técnicas data-driven como validação cruzada ou critérios de informação. O estimador LASSO é definido como:
Fluxo de trabalho
Aqui descrevemos brevemente os procedimentos adotados neste exercício de previsão, usando a linguagem de programação R:
- Carregar pacotes e dependências em um projeto de RStudio;
- Definir e carregar funções úteis;
- Importar dados brutos com base nos metadados das variáveis selecionadas;
- Tratar dados brutos de modo a obter uma tabela com as séries temporais do IPCA e as demais 33 variáveis exógenas, em frequência mensal;
- Testar a estacionariedade das variáveis exógenas e aplicar as transformações necessárias (diferenças);
- Criar base expandida com 1 até 4 defasagens de todas as variáveis;
- Contabilizar atrasos de publicação: preencher valores ausentes com última observação e remover séries de variáveis exógenas do momento presente (t), com exceção das expectativas do Focus;
- Adicionar dummies sazonais;
- Implementar validação cruzada1 partindo de 150 observações, acrescentando 1 observação e gerando 12 pontos de previsão pseudo out-of-sample, com finalidade de obter métricas de acurácia;
- Comparar a acurácia entre os modelos e benchmarks (Focus e Random Walk), usando o RMSE para escolha do modelo candidato para previsão fora da amostra;
- Reestimar o modelo candidato com a amostra completa de dados e gerar previsão fora da amostra;
- Visualização de resultados.
Dashboard de resultados
O resultado de todo o fluxo de trabalho deste exercício de previsão do IPCA é sintetizado e pode ser conferido nesta dashboard:
Saiba mais
Códigos de reprodução em R deste exercício estão disponíveis para membros do Clube AM da Análise Macro.
- Trilha de Macroeconomia Aplicada: https://conteudosam.com.br/pacotes/macroeconomia-aplicada/
- Trilha de Machine Learning e Econometria: https://conteudosam.com.br/pacotes/econometria-e-machine-learning/
- Modelos Preditivos: https://analisemacro.com.br/curso/modelos-preditivos-de-machine-learning/
- Econometria: https://analisemacro.com.br/cursos/econometria/introducao-a-econometria/
- Análise de Séries Temporais: https://conteudosam.com.br/cursos/analise-de-series-temporais/
Referências
Baybuza, I. (2018). Inflation forecasting using machine learning methods. Russian Journal of Money and Finance, 77(4), 42-59.
Choi, H., & Varian, H. (2012). Predicting the present with Google Trends. Economic record, 88, 2-9.
Elliott, G., Gargano, A., & Timmermann, A. (2013). Complete subset regressions. Journal of Econometrics, 177(2), 357-373.
Friedman, Jerome, Trevor Hastie, Robert Tibshirani, and others. (2001). The Elements of Statistical Learning. Vol. 1. 10. Springer series in statistics New York.
Garcia, M. G., Medeiros, M. C., & Vasconcelos, G. F. (2017). Real-time inflation forecasting with high-dimensional models: The case of Brazil. International Journal of Forecasting, 33(3), 679-693.
Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2022-04-01.
Kolassa, S. (2011). Combining exponential smoothing forecasts using Akaike weights. International Journal of Forecasting, 27(2), 238-251.
Mandalinci, Z. (2017). Forecasting inflation in emerging markets: An evaluation of alternative models. International Journal of Forecasting, 33(4), 1082-1104.
Marcelo C. Medeiros, Gabriel F. R. Vasconcelos, Álvaro Veiga & Eduardo Zilberman (2019). Forecasting Inflation in a Data-Rich Environment: The Benefits of Machine Learning Methods, Journal of Business & Economic Statistics, DOI: 10.1080/07350015.2019.1637745
Naccarato, A., Falorsi, S., Loriga, S., & Pierini, A. (2018). Combining official and Google Trends data to forecast the Italian youth unemployment rate. Technological Forecasting and Social Change, 130, 114-122.
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267-288.
Notas de rodapé
- Veja detalhes sobre validação cruzada no capítulo 5 de Hyndman e Athanasopoulos (2021).↩︎