A política monetária tem um papel importante na economia moderna, dispondo de diferentes instrumentos para alcançar a estabilidade estabilidade econômica, mantendo o controle sobre a inflação. A principal autoridade monetária do país utiliza desses artifícios, proporcionando mudanças através dos “canais de transmissão”, que são meios pelos quais a taxa básica de juros — a Selic — afeta outras variáveis macroeconômicas relevantes. Mas como saber o efeito dessa transmissão para a atividade econômica?
Artigo baseado no post “Como está a potência da política monetária no Brasil?”.
Aprenda a coletar, processar, analisar e modelar dados macroeconômicos no curso de Macroeconometria usando o Python.
Os instrumentos dispostos pela política monetária objetivam alcançar como metas finais o controle da inflação, a estabilidade do nível de atividade econômica, o gerenciamento da taxa de desemprego, bem como outras metas.
Isso é realizado através dos canais de transmissão, que são afetados por tais instrumentos, e consequentemente em segunda instância por mudanças na taxa básica de juros, a Selic. Entre os principais canais, temos: Consumo e investimento, Canal do Crédito, Expectativas, entre outros.
Mas como saber o efeito da tais mudanças da taxa de básica de juros sobre a atividade econômica? Na macroeconomia moderna é utilizada a chamada “curva IS” realizar essa comparação. Mais especificamente, a curva IS é uma equação que representa o lado da demanda agregada da economia e relaciona uma estimativa do hiato do produto com a taxa de juros real e outras variáveis.
O hiato do produto representa o componente cíclico da atividade econômica, ou seja, reflete condições conjunturais da economia, como choques de demanda/oferta, incentivos de política econômica, condições climáticas, choques externos, incertezas políticas, etc.
Sendo assim, para avaliar a transmissão da política monetária do canal da taxa de juros para a atividade econômica é necessário estimar uma curva IS. Neste exercício o objetivo é verificar se a relação esperada na teoria econômica (-) é encontrada com os dados brasileiros, além de verificar a evolução e a magnitude dessa relação ao longo do tempo.
Para tanto, estimamos uma Curva IS, baseando-se no Modelo Semiestrutural de pequeno porte do BCB (RI2021T2) para obter a sensibilidade da política monetária sobre a atividade econômica no Brasil.
Estimamos uma Curva IS que possui a seguinte forma:
onde:
= hiato do produto, medido como
= desvio do juro real ex ante, medido pela aplicação da equação de Fisher sobre a taxa dos contratos de swaps DI de 1 ano pela expectativa do IPCA no mesmo horizonte, em relação ao seu equilíbrio, medido como
é uma medida do resultado primário do governo central
corrigido pelo ciclo econômico e por outliers, e representado pelo desvio de sua tendência.
desvio da incerteza da economia, medida pelo IIE-Br, em relação ao seu equilíbrio.
= representa um choque aleatório de demanda.
Como foi realizado a estimação?
Para a construção do exercício seguimos o processo comum na análise de dados, que consiste da coleta e tratamento de dados, visualização, criação do modelo e comunicação dos resultados.
Os dados utilizados para cada variável foram:
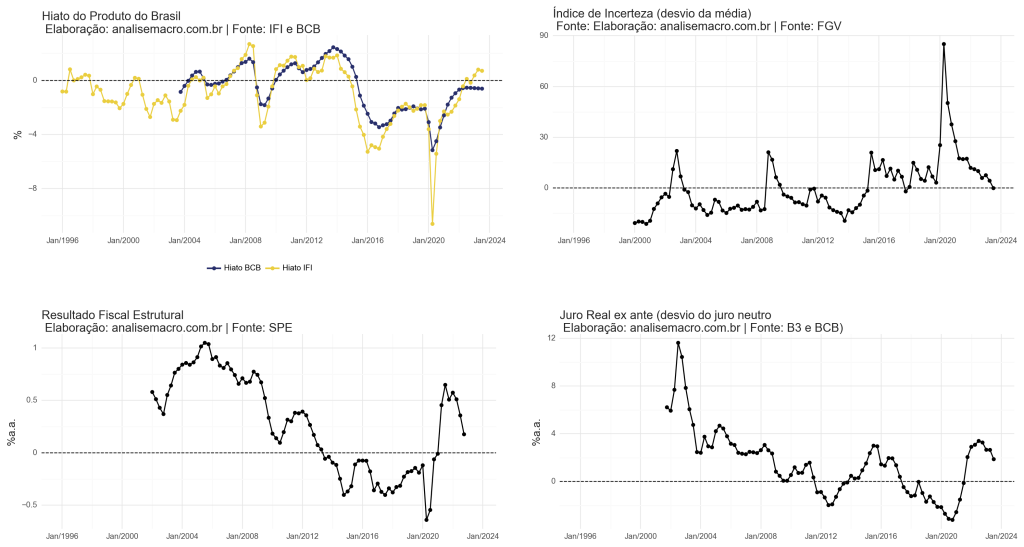
Hiato do Produto: o hiato é uma variável não observável, portanto, é necessário realizar da estimação da mesma, seja por filtros estatísticos ou função de produção. Tem sido um desafio nos últimos anos providenciar uma estimativa do hiato que seja um consenso entre as diferentes instituições, portanto, o presente exercício compara a utilização de duas estimativas, o Hiato produzido pela IFI, com resultado positivo nos trimestres de 2023 e o Hiato produzido pelo BCB, com resultado negativo nos trimestres 2023.
Desvio do juro real ex ante: para a taxa real fora utilizado a taxa dos contratos de swaps DI de 1 ano e a expectativa do IPCA no mesmo horizonte produzida pelo Focus. Para a taxa neutra (taxa de equilíbrio) fora utilizado as expectativas da Selic e do IPCA produzidos pelo Focus.
Resultado primário do governo central: utilizamos o Resultado Fiscal Estrutural produzido pela Secretária de Política Econômica.
Incerteza da Economia: IIE-br, produzida pela FGV.
A amostra dos dados segue 2002T2 até 2022T4 para a estimação do Hiato da IFI, e 2004T2 até 2022T4 para a estimação do Hiato do BCB.
Identificamos abaixo todas as variáveis representadas no modelo.
Em relação ao modelo utilizado, estimamos a Curva IS usando GMM com as defasagens de cada variável como instrumentos. Para encontrar a sensibilidade da política monetária sobre a atividade econômica, focamos na estimativa de , que espera-se ser negativa. Quanto mais negativo o valor de
, mais potente é a política monetária.
Produzimos um modelo "estático", isto é, com toda amostra, e um modelo em "janela móvel" com uma amostra em janelas deslizantes de 56 trimestres, com o objetivo de encontrar as mudanças de ao longo dos trimestres, e compreender a mudança da sensibilidade do coeficiente em diferentes períodos.
Resultados Econométricos
Os resultados estatísticos de ambas as especificações encontram-se nas tabelas abaixo. Vemos que o Modelo com Hiato do BCB apresentou uma relação de R² maior que o Modelo com Hiato da IFI, bem como os coeficientes estimados do primeiro modelos mostraram-se mais significantes. Entretanto, pela análise dos resíduos dos modelos, verificamos que o Modelo com Hiato da IFI apresentou-se melhor, em virtude da não presença de autocorrelação e uma distribuição menos assimétrica, em virtude de um grau menor de choques, ao contrário dos resíduos apresentados pelo Modelo com Hiato do BCB.
Em relação aos coeficientes dos , obtivemos resultados satisfatórios e esperados:
- Hiato (+)
- Hiato do Juros (-)
- IIE-br (-)
- Resultado Fiscal Estrutural (+)
Em relação a "potência" da política monetária, isto é, a magnitude do valor negativo do Hiato do Juros, verificamos um valor mais considerável no Modelo com Hiato do BCB.
Modelo com Hiato do BCB
| Dep. Variable: | hiato_bcb | R-squared: | 0.9633 |
| Estimator: | IV-GMM | Adj. R-squared: | 0.9612 |
| No. Observations: | 75 | F-statistic: | 2868.7 |
| Date: | Fri, Jan 05 2024 | P-value (F-stat) | 0.0000 |
| Time: | 13:50:42 | Distribution: | chi2(4) |
| Cov. Estimator: | robust | ||
| Parameter | Std. Err. | T-stat | P-value | Lower CI | Upper CI | |
| hiato_bcb_lag1 | 0.8217 | 0.0534 | 15.383 | 0.0000 | 0.7170 | 0.9264 |
| hiato_juros_lag1 | -0.1845 | 0.0347 | -5.3177 | 0.0000 | -0.2526 | -0.1165 |
| iie_diff | -0.0193 | 0.0097 | -2.0006 | 0.0454 | -0.0383 | -0.0004 |
| sup | 0.5336 | 0.0919 | 5.8081 | 0.0000 | 0.3535 | 0.7136 |
Endogenous: hiato_bcb_lag1, hiato_juros_lag1, iie_diff, sup
Instruments: hiato_bcb_lag2, hiato_juros_lag2, iie_diff_lag1, sup_lag1
GMM Covariance
Debiased: False
Robust (Heteroskedastic)
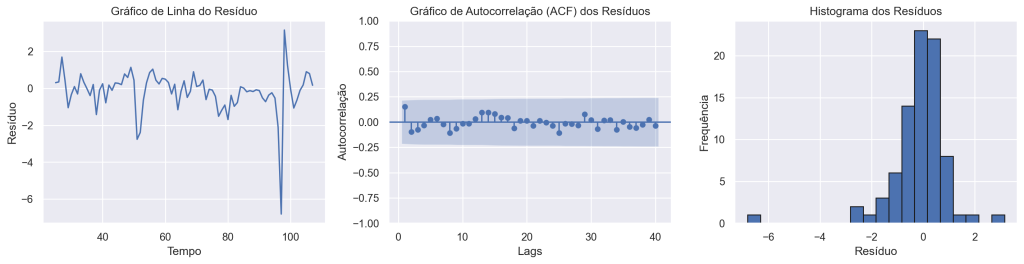
Análise dos Resíduos (Modelo BCB)
Modelo com Hiato da IFI
Código
| Dep. Variable: | hiato_ifi | R-squared: | 0.7927 |
| Estimator: | IV-GMM | Adj. R-squared: | 0.7822 |
| No. Observations: | 83 | F-statistic: | 337.58 |
| Date: | Fri, Jan 05 2024 | P-value (F-stat) | 0.0000 |
| Time: | 13:50:42 | Distribution: | chi2(4) |
| Cov. Estimator: | robust | ||
| Parameter | Std. Err. | T-stat | P-value | Lower CI | Upper CI | |
| hiato_ifi_lag1 | 0.7576 | 0.1289 | 5.8760 | 0.0000 | 0.5049 | 1.0103 |
| hiato_juros_lag1 | -0.1218 | 0.0578 | -2.1067 | 0.0351 | -0.2352 | -0.0085 |
| iie_diff | -0.0126 | 0.0361 | -0.3488 | 0.7272 | -0.0833 | 0.0581 |
| sup | 0.4195 | 0.3491 | 1.2018 | 0.2295 | -0.2647 | 1.1037 |
Endogenous: hiato_ifi_lag1, hiato_juros_lag1, iie_diff, sup
Instruments: hiato_ifi_lag2, hiato_juros_lag2, iie_diff_lag1, sup_lag1
GMM Covariance
Debiased: False
Robust (Heteroskedastic)
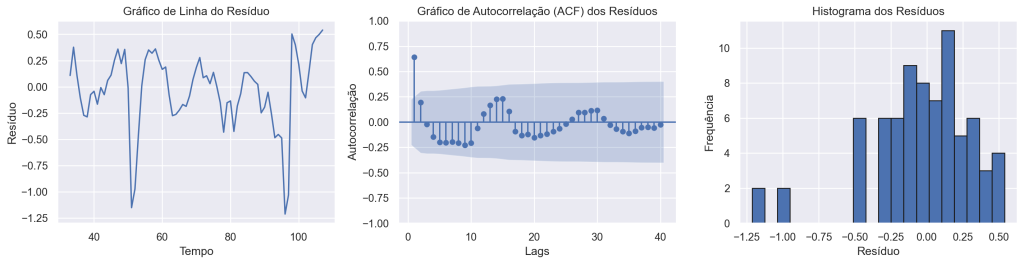
Análise dos Resíduos (Modelo IFI)
Comparação dos Modelos
| BCB | IFI | |
| Dep. Variable | hiato_bcb | hiato_ifi |
| Estimator | IV-GMM | IV-GMM |
| No. Observations | 75 | 83 |
| Cov. Est. | robust | robust |
| R-squared | 0.9633 | 0.7927 |
| Adj. R-squared | 0.9612 | 0.7822 |
| F-statistic | 2868.7 | 337.58 |
| P-value (F-stat) | 0.0000 | 0.0000 |
| ================== | =========== | =========== |
| hiato_bcb_lag1 | 0.8217 | |
| (15.383) | ||
| hiato_juros_lag1 | -0.1845 | -0.1218 |
| (-5.3177) | (-2.1067) | |
| iie_diff | -0.0193 | -0.0126 |
| (-2.0006) | (-0.3488) | |
| sup | 0.5336 | 0.4195 |
| (5.8081) | (1.2018) | |
| hiato_ifi_lag1 | 0.7576 | |
| (5.8760) | ||
| ==================== | ================== | ================== |
| Instruments | hiato_bcb_lag2 | hiato_ifi_lag2 |
| hiato_juros_lag2 | hiato_juros_lag2 | |
| iie_diff_lag1 | iie_diff_lag1 | |
| sup_lag1 | sup_lag1 |
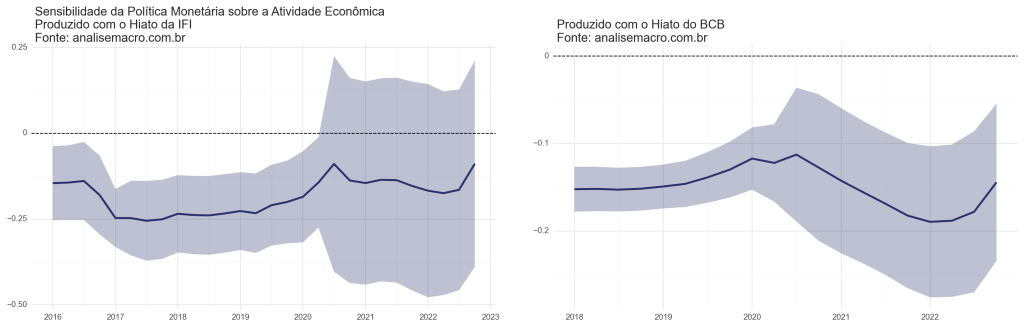
Modelo Econométrico em Janelas Móveis
Abaixo é apresentado os resultados do coeficiente ao longo de janelas móveis de 56 trimestres. Vemos que a magnitude tem se apresentado diferente entre os dois modelos, entretanto, há dois pontos em comum: o aumento da potência pós-covid, e a perda da mesma no fim de 2022.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.