Como mensurar retornos de ações no Python?

Este artigo tem como objetivo fornecer uma visão abrangente sobre como calcular medidas de retorno e risco no contexto de investimentos e ações, utilizando a linguagem de programação Python como ferramenta. Ao longo deste guia, detalharemos passo a passo as diversas métricas amplamente empregadas no mercado financeiro para avaliar a performance de investimentos e a volatilidade de ativos.

Um dos principais objetivos em finanças é avaliar e gerenciar os riscos associados a uma carteira de ativos financeiros. O risco, nesse contexto, é frequentemente medido em termos de variações nos preços dos ativos, uma vez que essas variações podem afetar o desempenho e a segurança dos investimentos. Essa avaliação de risco é fundamental para investidores e gestores de portfólio, pois ajuda a entender as possíveis oscilações nos valores dos ativos e permite a adoção de estratégias adequadas para mitigar tais riscos.

Na prática, é preferível trabalhar com retornos financeiros em vez de preços, uma vez que os retornos são medidas de taxa de variação e são livres de escala. Além disso, eles exibem propriedades estatísticas mais interessantes, como estacionariedade e ergodicidade, tornando-os mais adequados para análises e modelagem. Os retornos, ao refletirem as variações percentuais, proporcionam uma base sólida para compreender o comportamento dos ativos e suas relações no mercado financeiro, permitindo a identificação de padrões e tendências.

Portanto, um dos principais objetivos é modelar os retornos financeiros, e várias classes de modelos estatísticos podem ser empregadas para essa finalidade, incluindo modelos ARMA, ARCH, GARCH, e modelos de volatilidade estocástica. Esses modelos auxiliam na previsão de retornos futuros e na estimativa de riscos, sendo ferramentas valiosas para investidores e gestores de portfólio. Além disso, a análise de retornos desempenha um papel crucial na formulação de estratégias de investimento, na avaliação de ativos em diferentes cenários de mercado e na determinação de alocações de ativos adequadas, tornando-se um elemento-chave na tomada de decisões financeiras informadas.

Para entender melhor os conceitos de retorno e risco, é fundamental considerar as seguintes medidas:

Retornos:

Retorno Líquido Simples: Representa a variação percentual no valor de um ativo composto discretamente.
Retorno Bruto Simples: Indica a variação do retorno sem considerar o percentual.
Retorno Composto Continuamente (log-retorno): É uma medida que envolve o uso de logaritmos e é especialmente útil em cálculos contínuos, como a análise de ativos ao longo do tempo.
Retorno Geométrico: Representa o retorno médio ponderado ao longo de vários períodos, levando em consideração a taxa composta de crescimento ao longo do tempo.

Retornos Acumulados:

Retorno simples multiperíodos: É a variação percentual no valor de um ativo ao longo de múltiplos períodos, calculada acumulativamente.
Retorno Composto Continuamente (log-retorno) multiperíodos: Reflete a variação contínua no valor de um ativo em vários períodos, considerando o crescimento ao longo do tempo.

Retorno Anualizado:

Retorno Anualizado para Retornos Simples: É a taxa de retorno média anual, considerando retornos simples ao longo de um período.
Retorno Anualizado para Retornos Geométricos: Representa a taxa de retorno média anual, considerando retornos geométricos ao longo de um período.
Retorno Anualizado em Janelas Deslizantes: Calcula a taxa de retorno média anualizada em períodos móveis, útil para análise de tendências e volatilidade ao longo do tempo.

Volatilidade:

Desvio Padrão: É uma medida que avalia a dispersão dos retornos de um ativo, indicando o grau de volatilidade.
Desvio Padrão Anualizado: É o desvio padrão dos retornos ajustado para um período anual, tornando-o comparável em uma base anual.
Desvio Padrão Móvel: Calcula o desvio padrão dos retornos em janelas deslizantes, permitindo uma análise da volatilidade ao longo do tempo.

O Python pode ser uma ferramenta útil para verificarmos cada medida citada acima. Como exemplo, utilizaremos dados do preço de fechamento diário do Ibovespa no período de 2018 até fim de 2022. Coletamos os dados através do Yahoo Finance pelo ticker ‘^BVSP’.

Alunos inscritos no curso de Mercado Financeiro e Gestão de Portfólio com o Python têm a oportunidade de adquirir conhecimento em todas as etapas a seguir, além de obter uma compreensão teórica abrangente das principais ferramentas utilizadas no Mercado Financeiro.

Retornos:

1. Retorno Líquido Simples:

- A variação de preços entre os instantes $t-1$ e $t$ é dada por $\Delta P_t = P_t - P_{t-1}$ .
- A variação relativa de preços ou retorno líquido simples deste ativo entre os mesmos instantes é definida como: $R_t = \Delta P_t / P_{t-1}$ . É também chamada de Taxa de Retorno.
- Formulação matemática: $R_t = \frac{P_t - P_{t-1}}{P_{t-1}}$

2. Retorno Bruto Simples:

- Chamamos $1 + R_t = P_t / P_{t-1}$ de retorno bruto simples.
- O retorno bruto simples representa a variação de preços de um ativo sem a representação de taxas percentuais.
- Formulação matemática: $1 + R_t = \frac{P_t}{P_{t-1}}$

Código

	retorno_simples	retorno_bruto_simples
Date
2018-01-02	NaN	NaN
2018-01-03	0.001335	1.001335
2018-01-04	0.008360	1.008360
2018-01-05	0.005391	1.005391
2018-01-08	0.003895	1.003895
...	...	...
2022-12-23	0.022187	1.022187
2022-12-26	-0.008751	0.991249
2022-12-27	-0.003596	0.996404
2022-12-28	0.017444	1.017444
2022-12-29	-0.001869	0.998131

1238 rows × 2 columns

3. Retorno Composto Continuadamente (Log-Retorno):

- Usado para avaliar o desempenho de um investimento ao longo de um período contínuo.
- Calculado usando logaritmos naturais e a fórmula: $r_t = \ln\left(\frac{P_t}{P_{t-1}}\right)$

Código

	retorno_simples	retorno_bruto_simples	log_retorno
Date
2018-01-02	NaN	NaN	NaN
2018-01-03	0.001335	1.001335	0.001334
2018-01-04	0.008360	1.008360	0.008325
2018-01-05	0.005391	1.005391	0.005377
2018-01-08	0.003895	1.003895	0.003888
...	...	...	...
2022-12-23	0.022187	1.022187	0.021944
2022-12-26	-0.008751	0.991249	-0.008790
2022-12-27	-0.003596	0.996404	-0.003602
2022-12-28	0.017444	1.017444	0.017294
2022-12-29	-0.001869	0.998131	-0.001870

1238 rows × 3 columns

4. Retorno Médio Aritmético:

- Calcula para obter o retorno médio de uma determinado período em um intervalo. Exemplo: em média, qual foi o retorno diário de uma ação durante um período?
- Calcula através de uma média simples: $\frac{1}{N-1}\Sigma_{i=1}^N R_t$
onde $N$ é tamanho da amostra/série.

Para o caso do Ibovespa no período temos o valor de:

Código

0.000427414617205675

5. Retorno Médio Geométrico:

- Calculado para investimentos de longo prazo, levando em consideração o reinvestimento de ganhos. Basicamente, é o retorno médio composto em todo o período de investimento
- Representa o crescimento composto e é calculado como: $\text{Retorno Geométrico} = \left[(1 + R_t) \cdot (1 + R_{t-1}) \cdot \ldots \cdot (1 + R_1)\right]^{\frac{1}{N}} - 1$

Para o caso do Ibovespa no período temos o valor de:

Código

0.00027930474673532046

Retornos Acumulados:

6. Retorno Simples Multiperíodos:

- Calculado para avaliar o desempenho de um investimento ao longo de vários períodos.
- Usado para somar os retornos simples em cada período.
- Formulação matemática: $\text{Retorno Simples Multiperíodos} = \prod_{i=1}^{N} (1 + R_i) - 1$

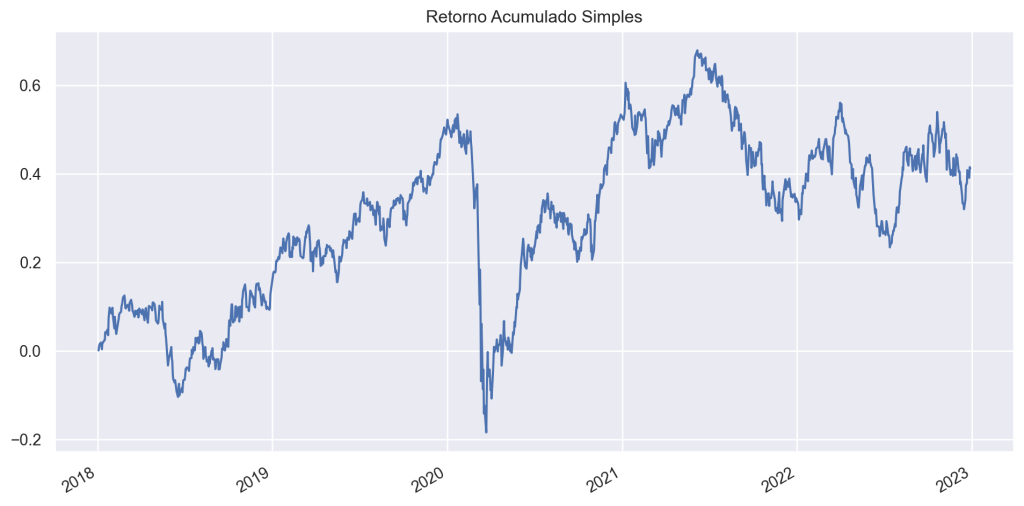
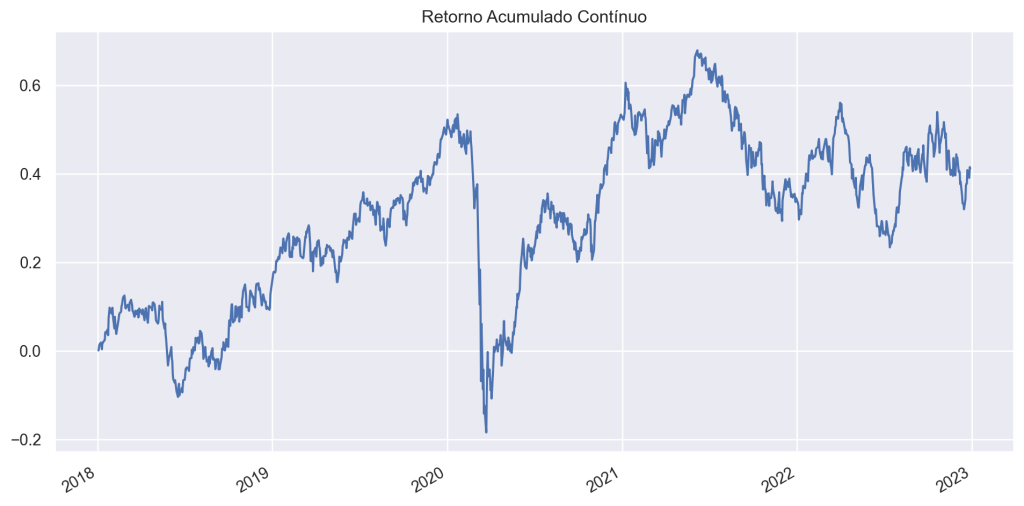
Para o caso do Ibovespa, o Retorno Acumulado no período é de:

Código

0.41262790309535013

É possível acumular os valores em cada período até o fim da amostra, como demonstra o gráfico abaixo:

7. Retorno Composto Continuadamente (Log-Retorno) Multiperíodos:

- Usado para avaliar o desempenho de um investimento ao longo de múltiplos períodos de forma contínua.
- Calculado somando os log-retornos de cada período.
- Formulação matemática: $\text{Log-Retorno Multiperíodos} = \Sigma_{i=1}^Nr_t$

Para o caso do Ibovespa, o Retorno Acumulado Continuadamente no período é de:

Código

0.34545173080294256

Retorno Anualizado:

8. Retorno Anualizado para Retornos Simples:

- Utilizado para expressar o retorno de um investimento em uma base anual, mesmo que o período de investimento seja menor que um ano.
- Calculado multiplicando o retorno simples pelo número de períodos em um ano.
- Formulação matemática: $\text{Retorno Anualizado Simples} = \frac{1}{N-1}\Sigma_{i=1}^N R_t \times 252$

Para o caso do Ibovespa no período, temos o seguinte valor:

Código

0.1077084835358301

9. Retorno Anualizado para Retornos Geométricos:

- Usado para calcular o retorno anualizado de investimentos de longo prazo que consideram o reinvestimento de ganhos.
- Calculado usando a fórmula (para o caso de diário, com 252 dias úteis): $\text{Retorno Anualizado Geométrico} = \left[(1 + R_t) \cdot (1 + R_{t-1}) \cdot \ldots \cdot (1 + R_1)\right]^{\frac{252}{N}} - 1$

Para o caso do Ibovespa no período, temos o seguinte valor:

Código

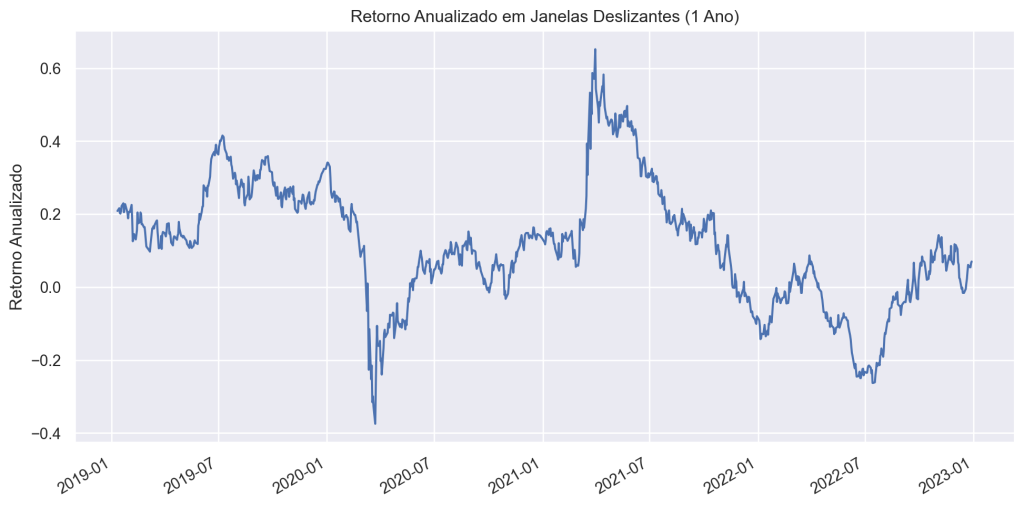
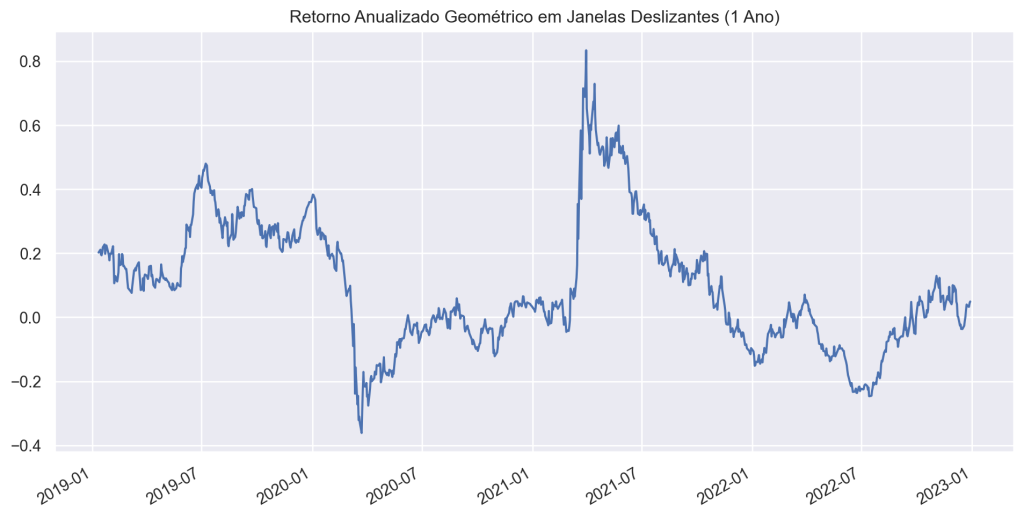
0.07291041355654992

10. Retorno Anualizado em Janelas Deslizantes

- Calcula a taxa de retorno média anualizada em períodos móveis, útil para análise de tendências e volatilidade ao longo do tempo.
- Para calcular o retorno anualizado móvel em uma janela deslizante, você calcula o retorno anualizado para cada janela e move a janela ao longo do conjunto de dados.
- A fórmula é a seguinte para o aritmético e geométrico, respectivamente:

$\text{Retorno Anualizado Simples} = \frac{1}{T-1}\Sigma_{i=1}^N R_t \times 252$

$\text{Retorno Anualizado Geométrico} = \left[(1 + Retorno\,Geométrico)^{\frac{252}{T}} - 1\right]$

Onde:

- $T$ é o tamanho fixo da janela (por exemplo, 252 para um ano ou 22 para um mês).

Volatilidade

1. Desvio Padrão (Volatilidade):

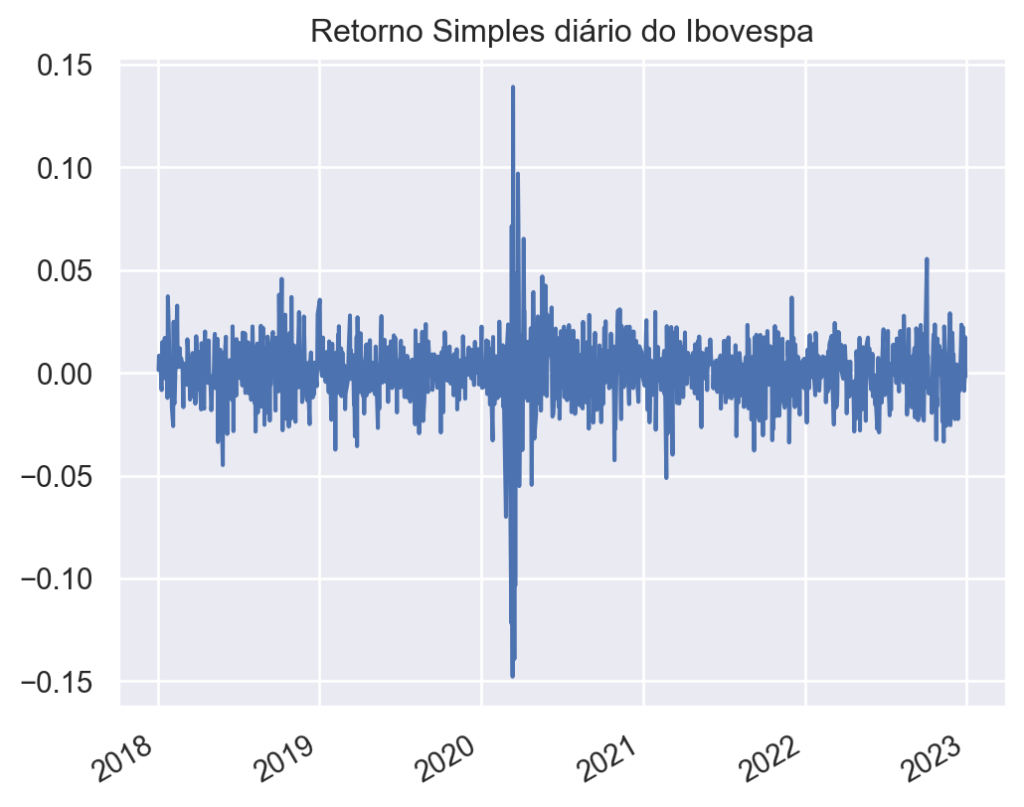
O desvio padrão é uma medida de dispersão que indica a variabilidade dos retornos de um ativo ou investimento. Ele mede o grau de volatilidade do ativo.

**Fórmula:**
O desvio padrão é calculado da seguinte maneira para uma série de retornos:

$\text{Desvio Padrão} = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N} (R_i - \overline{R})^2}$

Onde:

- $N$ é o número de observações (dias, meses, anos, etc.).

- $R_i$ é o retorno no período $i$ .

- $\overline{R}$ é a média dos retornos.

O desvio padrão diário em toda a amostra dos retornos do Ibovespa no período foi de:

Código

0.017108656414304535

2. Desvio Padrão Anualizado:

O desvio padrão anualizado é o desvio padrão dos retornos ajustado para um período anual. Isso é útil para comparar a volatilidade em uma base anual.

Fórmula:
Para anualizar o desvio padrão, você multiplica o desvio padrão da série de retornos por uma raiz quadrada do número de períodos em um ano (geralmente 252 para dias de negociação ou 12 para meses).

$\text{Desvio Padrão Anualizado} = \text{Desvio Padrão} \times \sqrt{N}$

Onde $N$ é o número de períodos de observação em um ano (por exemplo, 252 para dados diários e 12 para meses).

Código

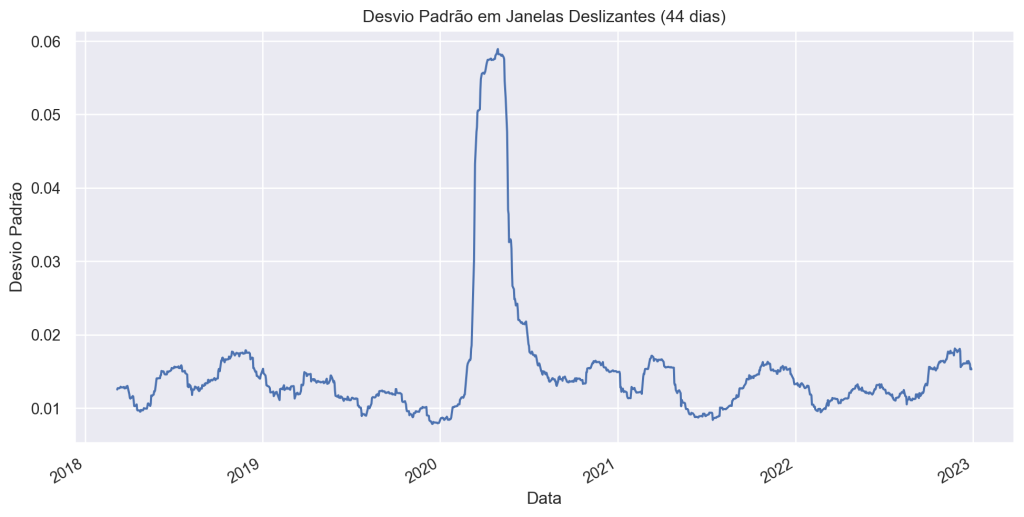
0.2715915008321991

3. Desvio Padrão Móvel (ou Desvio Padrão em Janelas Deslizantes):

O desvio padrão móvel é usado para avaliar a volatilidade ao longo do tempo, calculando o desvio padrão em janelas deslizantes (móveis) de dados.

Fórmula:
Para calcular o desvio padrão móvel em uma janela deslizante, você calcula o desvio padrão para cada janela e move a janela ao longo do conjunto de dados.

$\text{Desvio Padrão Móvel} = \sqrt{\frac{1}{T-1} \sum_{i=1}^{T} (R_i - \overline{R})^2}$

Onde:

- $T$ é o tamanho da janela (por exemplo, 252 para um ano ou 22 para um mês).

- $R_i$ são os retornos dentro da janela.

- $\overline{R}$ é a média dos retornos dentro da janela.

Para o caso do Ibovespa, os seguintes valores para o desvio padrão em janelas deslizantes de 44 dias, tanto diário, quanto anualizado se encontram nos respectivos gráficos abaixo:

Quer aprender mais?

Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

Referências

Morettin, P. A.. Econometria financeira: um curso em séries temporais financeiras. Editora Blucher. 3 ed. 2017.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise exploratória para modelagem preditiva no Python

Como usar modelos do Sklearn para previsão? Uma introdução ao Skforecast

Métodos de Reamostragem de Séries Temporais no Python

Coletando dados regionais do CAGED no Python

Coletando dados de Setores Censitários do Censo 2022 no Python

Estimando a inércia inflacionária através de modelos de espaço-estado usando Python

Outros artigos relacionados

Análise exploratória para modelagem preditiva no Python

Antes de desenvolver bons modelos preditivos é necessário organizar e conhecer muito bem os dados. Neste artigo, damos algumas dicas de recursos, como gráficos, análises e estatísticas, que podem ser usados para melhorar o entendimento sobre os dados usando Python.

Como usar modelos do Sklearn para previsão? Uma introdução ao Skforecast

Prever séries temporais é uma tarefa frequente em diversas áreas, porém exige conhecimento e ferramentas específicas. Os modelos de machine learning do Sklearn são populadores, porém são difíceis de aplicar em estruturas temporais de dados. Neste sentido, introduzimos a biblioteca Skforecast, que integra os modelos do Sklearn e a previsão de séries temporais de forma simples.

Métodos de Reamostragem de Séries Temporais no Python

Nesta postagem, vamos mostrar alguns métodos simples para lidar com a reamostragem de dados de séries temporais no Python.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!