Em quanto um choque cambial afeta a inflação? Analisando funções impulso-resposta no VAR usando Python

É conhecido na macroeconomia que variações na taxa de câmbio são repassadas para o nível de preços ao consumidor, o efeito “pass-through”. Isso significa que um aumento repentino na taxa de câmbio, de um desvio padrão por exemplo, tende a afetar os preços da cesta de produtos e serviços ao consumidor, aumentando assim a taxa de inflação nos próximos períodos. Quantificar este repasse cambial é, portanto, importante para compreender a dinâmica da inflação na economia.

Este exercício quantifica o repasse cambial sobre a inflação para a economia brasileira sob a ótica de um modelo VAR. Usando dados recentes, estimamos as funções de impulso resposta para analisar choques na variação do câmbio e a resposta ao longo do tempo sobre a inflação de preços livres.

Esse exercício é uma tradução para Python da postagem “Em quanto um choque cambial afeta a inflação? Analisando funções impulso-resposta no VAR”.

Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.

Modelo

Com o propósito de quantificar o repasse cambial, nos inspiramos em BCB (2018) representando uma Curva de Phillips para a inflação de preços livres estimada por um modelo VAR, como abaixo:

$y_t = \sum_{i\ge0}^p A_p y_{t-p} + z_t + \varepsilon_t$

onde:

- $y_t = (\pi_t^L, E_t \pi_{t+i}, \pi_t, \Delta e_t, h_t)$

- $\pi_t^L$ é a inflação de preços livres do IPCA

- $E_t \pi_{t+i}$ é a inflação esperada no momento $t$ para o IPCA $i$ momentos à frente

- $\pi_t$ é a inflação do IPCA

- $\Delta e_t$ é a variação da taxa de câmbio nominal (R$/US$)

- $h_t$ é uma medida de hiato do produto

- $z_t$ é uma variável de controle que pode incluir constante, tendência e/ou dummies sazonais

Funções impulso resposta

As funções impulso resposta (FIR) respondem a seguinte pergunta:

- Qual é a resposta ao longo do tempo em uma variável endógena de um modelo VAR para um choque em outra variável, assumindo que os choques de outras variáveis são nulos?

Dessa forma, a FIR permite isolar o efeito de um choque em termos de sinal e magnitude ao longo do tempo, mantendo tudo o mais constante.

Para calcular FIR, considere um simples modelo VAR com apenas uma defasagem, tal como:

$y_t = A y_{t-1} + \varepsilon_t$

Para encontrar, por exemplo, o efeito do *j*-ésimo elemento do vetor de choques $\varepsilon$ sobre o *i*-ésimo elemento do vetor de variáveis endógenas $y$ após dois períodos, que é uma resposta ao impulso específica, primeiro reescreva a equação acima com uma defasagem, tal como:

$y_{t-1} = A y_{t-2} + \varepsilon_{t-1}$

Substituindo, obtemos:

$y_t = A^2 y_{t-2} + A \varepsilon_{t-1} + \varepsilon_t$

Então repetimos o processo usando duas defasagens para obter:

$y_t = A^3 y_{t-3} + A^2 \varepsilon_{t-2} + A \varepsilon_{t-1} + \varepsilon_t$

Dessa forma, o efeito do *j*-ésimo elemento de $\varepsilon_{t-2}$ sobre o *i*-ésimo elemento de $y_t$ é o *i, j* elemento da matriz $A^2$ .

Dados

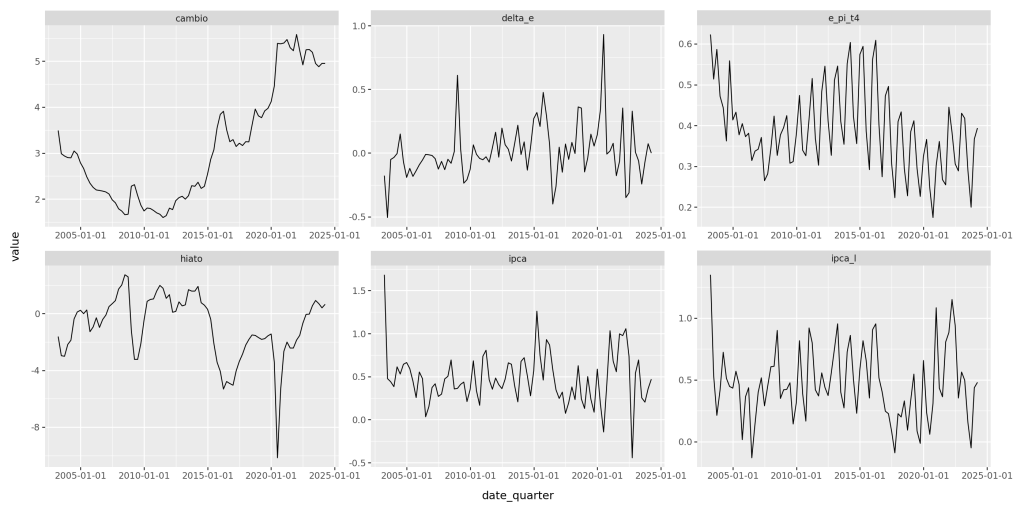
Utilizamos uma amostra de dados do quarto trimestre de 2003 ao quarto trimestre de 2023. Os dados em frequência trimestral são expostos no gráfico abaixo:

Ordem de Integração

Confirmamos a ordem de integração das séries através de testes de estacionariedade ADF, PP e KPSS. Abaixo reportamos a ordem de integração reportada entre os testes para cada variável:

Código

	kpss	adf	pp
ipca_l	0	1	0
ipca	0	1	0
delta_e	1	0	0
hiato	1	1	1
e_pi_t4	1	1	0

Cointegração

Devemos verificar a ordem de defasagem baseando-se em critérios de informação. Além disso, o sinal True, revela que o modelo é um VECM, ao invés de um VAR:

{'aic': 8, 'bic': 0, 'hqic': 3, 'fpe': 4}
True

Abaixo reportamos os resultados para o teste do máximo autovalor:

Código

Johansen cointegration test using maximum eigenvalue test statistic with 5% significance level
=====================================
r_0 r_1 test statistic critical value
-------------------------------------
  0   1          60.66          30.44
  1   2          40.69          24.16
  2   3          32.58          17.80
  3   4          9.316          11.22
-------------------------------------
Rank :  3

Modelagem

Encontramos cointegração com posto da matriz igual a 3 e, dessa forma, estimamos um modelo VECM usando defasagens definidas por critérios de informação:

Código

Det. terms outside the coint. relation & lagged endog. parameters for equation ipca_l
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
season1        0.3732      0.067      5.582      0.000       0.242       0.504
season2        0.1906      0.067      2.848      0.004       0.059       0.322
season3       -0.0718      0.067     -1.078      0.281      -0.202       0.059
Det. terms outside the coint. relation & lagged endog. parameters for equation ipca
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
season1        0.2986      0.070      4.292      0.000       0.162       0.435
season2        0.1615      0.070      2.319      0.020       0.025       0.298
season3       -0.0785      0.069     -1.133      0.257      -0.214       0.057
Det. terms outside the coint. relation & lagged endog. parameters for equation delta_e
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
season1        0.0206      0.064      0.323      0.746      -0.104       0.145
season2       -0.0457      0.064     -0.717      0.474      -0.171       0.079
season3       -0.0408      0.063     -0.643      0.520      -0.165       0.084
Det. terms outside the coint. relation & lagged endog. parameters for equation hiato
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
season1       -0.0085      0.381     -0.022      0.982      -0.755       0.738
season2       -0.1970      0.381     -0.517      0.605      -0.944       0.550
season3       -0.4692      0.379     -1.237      0.216      -1.213       0.275
Det. terms outside the coint. relation & lagged endog. parameters for equation e_pi_t4
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
season1        0.1424      0.021      6.791      0.000       0.101       0.184
season2        0.0504      0.021      2.400      0.016       0.009       0.092
season3       -0.1080      0.021     -5.165      0.000      -0.149      -0.067
               Loading coefficients (alpha) for equation ipca_l               
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1           -0.5247      0.158     -3.311      0.001      -0.835      -0.214
ec2            0.0374      0.151      0.248      0.804      -0.258       0.333
ec3            0.1814      0.115      1.581      0.114      -0.043       0.406
                Loading coefficients (alpha) for equation ipca                
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1            0.1326      0.165      0.804      0.421      -0.191       0.456
ec2           -0.7524      0.157     -4.798      0.000      -1.060      -0.445
ec3            0.2240      0.119      1.877      0.061      -0.010       0.458
              Loading coefficients (alpha) for equation delta_e               
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1           -0.0217      0.151     -0.144      0.885      -0.317       0.274
ec2           -0.0226      0.143     -0.157      0.875      -0.304       0.259
ec3           -0.7022      0.109     -6.429      0.000      -0.916      -0.488
               Loading coefficients (alpha) for equation hiato                
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1            1.1886      0.903      1.317      0.188      -0.580       2.958
ec2           -1.3531      0.858     -1.576      0.115      -3.035       0.329
ec3           -0.9326      0.653     -1.428      0.153      -2.213       0.348
              Loading coefficients (alpha) for equation e_pi_t4               
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1            0.1303      0.050      2.621      0.009       0.033       0.228
ec2           -0.0535      0.047     -1.132      0.257      -0.146       0.039
ec3            0.0066      0.036      0.185      0.853      -0.064       0.077
          Cointegration relations for loading-coefficients-column 1           
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
beta.1         1.0000          0          0      0.000       1.000       1.000
beta.2      2.302e-17          0          0      0.000     2.3e-17     2.3e-17
beta.3     -5.462e-19          0          0      0.000   -5.46e-19   -5.46e-19
beta.4        -0.0100      0.015     -0.662      0.508      -0.040       0.020
beta.5        -1.2122      0.014    -85.190      0.000      -1.240      -1.184
          Cointegration relations for loading-coefficients-column 2           
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
beta.1     -3.532e-17          0          0      0.000   -3.53e-17   -3.53e-17
beta.2         1.0000          0          0      0.000       1.000       1.000
beta.3      1.084e-16          0          0      0.000    1.08e-16    1.08e-16
beta.4         0.0029      0.010      0.280      0.779      -0.017       0.023
beta.5        -1.1938      0.091    -13.083      0.000      -1.373      -1.015
          Cointegration relations for loading-coefficients-column 3           
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
beta.1     -1.601e-17          0          0      0.000    -1.6e-17    -1.6e-17
beta.2     -2.677e-17          0          0      0.000   -2.68e-17   -2.68e-17
beta.3         1.0000          0          0      0.000       1.000       1.000
beta.4         0.0125      0.086      0.146      0.884      -0.155       0.180
beta.5        -0.0233      0.062     -0.374      0.708      -0.145       0.099
==============================================================================

Realizamos abaixo os testes autocorrelação e normalidade.

Código

Portmanteau-test for residual autocorrelation. H_0: residual autocorrelation up to lag 20 is zero. Conclusion: fail to reject H_0 at 5% significance level.
=========================================
Test statistic Critical value p-value  df
-----------------------------------------
         534.4          537.3   0.060 485
-----------------------------------------

Código

normality (skew and kurtosis) test. H_0: data generated by normally-distributed process. Conclusion: reject H_0 at 5% significance level.
========================================
Test statistic Critical value p-value df
----------------------------------------
         252.9          18.31   0.000 10
----------------------------------------

Pelos resultados, o resíduos não apresentaram autocorrelação significativa até a defasagem 20. Entretanto, os resíduos não estão normalmente distribuídos. Ignoraremos este problema aqui, enfatizando que intervalos de confiança calculados a partir deste modelo podem ser imprecisos.

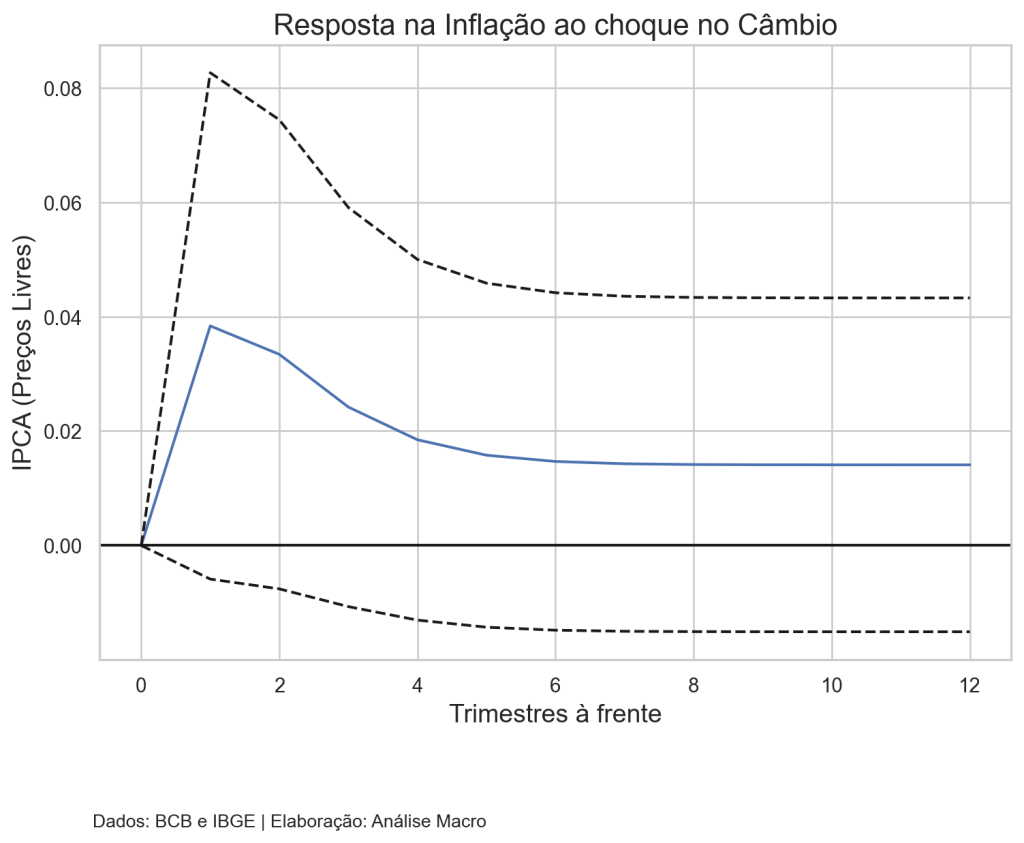
Os principais resultados são os seguintes:

Choques cambiais não são repassados instantaneamente para o nível de preços;
O efeito dos choques cambiais sobre a inflação de preços livres tende a ser positivo;
Um choque de um desvio padrão na variação da taxa de câmbio tem um efeito inicial pequeno, mas persistente ao longo do tempo;

Conclusão

Referências

BANCO CENTRAL DO BRASIL (2018). Repasse cambial sob a ótica de um modelo semiestrutural. Box do Relatório de Inflação de Setembro de 2018.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Métodos de Reamostragem de Séries Temporais no Python

Coletando dados regionais do CAGED no Python

Coletando dados de Setores Censitários do Censo 2022 no Python

Estimando a inércia inflacionária através de modelos de espaço-estado usando Python

Criando um Dashboard de Análise de Dados de Demonstrativos Financeiros no Python

IPCA de outubro surpreende mercado, mas fica em linha com a previsão da Análise Macro

Outros artigos relacionados

Métodos de Reamostragem de Séries Temporais no Python

Nesta postagem, vamos mostrar alguns métodos simples para lidar com a reamostragem de dados de séries temporais no Python.

Coletando dados regionais do CAGED no Python

Os dados regionais do CAGED permitem analisar o mercado de trabalho de forma detalhada, em termos de setores, educação, rendimento e características pessoais dos trabalhadores brasileiros. Neste exercício mostramos como acessar estas informações online via Python.

Coletando dados de Setores Censitários do Censo 2022 no Python

Dados sobre a demografia e o território são primordiais para definir e implementar políticas públicas, áreas de atuação comercial e/ou estratégias de marketing. Sendo assim, saber usar os dados do Censo 2022 pode trazer vantagens competitivas. Neste exercício mostramos como obter os dados da Malha de Setores Censitários no formato vetorial (GeoJson) usando o Python.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!