Em quanto um choque cambial afeta a inflação? Analisando funções impulso-resposta no VAR

É conhecido na macroeconomia que variações na taxa de câmbio são repassadas para o nível de preços ao consumidor, o efeito “pass-through”. Isso significa que um aumento repentino na taxa de câmbio, de um desvio padrão por exemplo, tende a afetar os preços da cesta de produtos e serviços ao consumidor, aumentando assim a taxa de inflação nos próximos períodos. Quantificar este repasse cambial é, portanto, importante para compreender a dinâmica da inflação na economia.

Este exercício quantifica o repasse cambial sobre a inflação para a economia brasileira sob a ótica de um modelo VAR. Usando dados recentes, estimamos as funções de impulso resposta para analisar choques na variação do câmbio e a resposta ao longo do tempo sobre a inflação de preços livres.

Modelo

Com o propósito de quantificar o repasse cambial, nos inspiramos em BCB (2018) representando uma Curva de Phillips para a inflação de preços livres estimada por um modelo VAR, como abaixo:

$y_t = \sum_{i\ge0}^p A_p y_{t-p} + z_t + \varepsilon_t$

onde:

$y_t = (\pi_t^L, E_t \pi_{t+i}, \pi_t, \Delta e_t, h_t)$
$\pi_t^L$ é a inflação de preços livres do IPCA
$E_t \pi_{t+i}$ é a inflação esperada no momento $t$ para o IPCA $i$ momentos à frente
$\pi_t$ é a inflação do IPCA
$\Delta e_t$ é a variação da taxa de câmbio nominal (R$/US$)
$h_t$ é uma medida de hiato do produto
$z_t$ é uma variável de controle que pode incluir constante, tendência e/ou dummies sazonais

Aprenda mais sobre modelos VAR, SVAR, VECM, SVEC, ARIMA e outros através do curso de Análise de Séries Temporais da Análise Macro.

Funções impulso resposta

As funções impulso resposta (FIR) respondem a seguinte pergunta:

Qual é a resposta ao longo do tempo em uma variável endógena de um modelo VAR para um choque em outra variável, assumindo que os choques de outras variáveis são nulos?

Dessa forma, a FIR permite isolar o efeito de um choque em termos de sinal e magnitude ao longo do tempo, mantendo tudo o mais constante.

Para calcular FIR, considere um simples modelo VAR com apenas uma defasagem, tal como:

$y_t = A y_{t-1} + \varepsilon_t$

(1)

Para encontrar, por exemplo, o efeito do j-ésimo elemento do vetor de choques $\varepsilon$ sobre o i-ésimo elemento do vetor de variáveis endógenas $y$ após dois períodos, que é uma resposta ao impulso específica, primeiro reescreva a equação acima com uma defasagem, tal como:

$y_{t-1} = A y_{t-2} + \varepsilon_{t-1}$

(2)

Substituindo (1) em (2), obtemos:

$y_t = A^2 y_{t-2} + A \varepsilon_{t-1} + \varepsilon_t$

Então repetimos o processo usando duas defasagens da (1) para obter:

$y_t = A^3 y_{t-3} + A^2 \varepsilon_{t-2} + A \varepsilon_{t-1} + \varepsilon_t$

Dessa forma, o efeito do j-ésimo elemento de $\varepsilon_{t-2}$ sobre o i-ésimo elemento de $y_t$ é o i, j elemento da matriz $A^2$ .

Dados

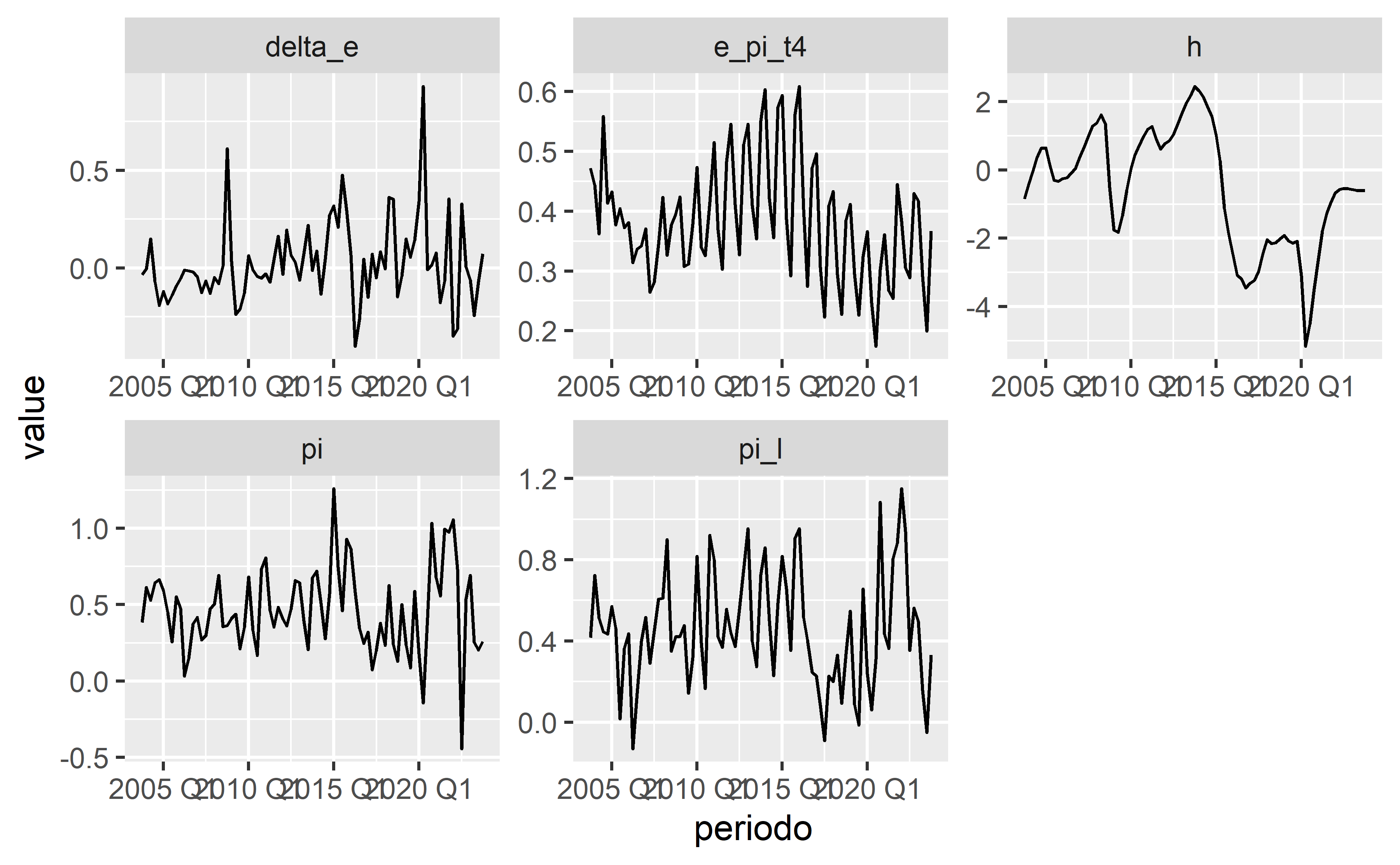
Utilizamos uma amostra de dados do quarto trimestre de 2003 ao quarto trimestre de 2023. Os dados em frequência trimestral são expostos no gráfico abaixo:

Para obter o código deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.

Algumas das variáveis selecionadas apresentam visualmente comportamento não estacionário, o que é problemático para a modelagem VAR.

Exploração

Confirmamos a ordem de integração das séries através de testes de estacionariedade ADF, PP e KPSS com constante e com tendência. Como são 3 testes e 2 especificações possíveis, foram aplicados 6 testes individualmente para cada variável. Abaixo reportamos a ordem de integração mais frequentemente reportada entre os testes para cada variável:

# A tibble: 5 × 3
  variavel ordem_integracao     n
  <chr>               <dbl> <int>
1 delta_e                 0     6
2 e_pi_t4                 0     4
3 h                       1     6
4 pi                      0     6
5 pi_l                    0     6

Encontramos que o hiato do produto é integrado de ordem 1 e as demais são de ordem 0. Neste cenário, prosseguimos investigando se há cointegração entre as séries temporais usando o teste de Johansen. Abaixo reportamos os resultados para o teste do máximo autovalor:


###################### 
# Johansen-Procedure # 
###################### 

Test type: maximal eigenvalue statistic (lambda max) , without linear trend and constant in cointegration 

Eigenvalues (lambda):
[1] 5.710011e-01 3.608327e-01 2.625436e-01 7.659799e-02 5.079090e-02
[6] 3.155246e-16

Values of teststatistic and critical values of test:

          test 10pct  5pct  1pct
r <= 4 |  4.01  7.52  9.24 12.97
r <= 3 |  6.14 13.75 15.67 20.20
r <= 2 | 23.45 19.77 22.00 26.81
r <= 1 | 34.46 25.56 28.14 33.24
r = 0  | 65.17 31.66 34.40 39.79

Eigenvectors, normalised to first column:
(These are the cointegration relations)

              pi_l.l4        h.l4  e_pi_t4.l4       pi.l4 delta_e.l4
pi_l.l4     1.0000000  1.00000000  1.00000000  1.00000000  1.0000000
h.l4        0.1259625 -0.04214096 -0.08210039 -0.30625473 -0.1702272
e_pi_t4.l4 -2.9525718  0.85707996  0.57965592  6.16931502 -9.8621368
pi.l4       0.3550030 -1.15098817  0.61460879  0.09763306  0.3651735
delta_e.l4  1.7231035 -0.24761985 -2.78132276  2.19154376 -1.3483273
constant    0.4647494 -0.26844156 -0.92374229 -2.97502445  2.8674561
              constant
pi_l.l4      1.0000000
h.l4         0.5449363
e_pi_t4.l4 -30.7206454
pi.l4        1.5061414
delta_e.l4  -0.9496715
constant    13.4237085

Weights W:
(This is the loading matrix)

               pi_l.l4        h.l4   e_pi_t4.l4        pi.l4   delta_e.l4
pi_l.d     0.007250229 -0.70346355 -0.226205481 -0.010183368  0.009074012
h.d       -0.103567765  0.66620508 -0.222536824  0.089788517  0.098207292
e_pi_t4.d  0.087292358 -0.03856738 -0.008233752 -0.005005917  0.003069083
pi.d       0.069897003  0.17836622 -0.300326881 -0.009456894 -0.006626427
delta_e.d -0.085935885 -0.16150921  0.096104858 -0.098732276 -0.015202148
               constant
pi_l.d     1.177799e-16
h.d        7.575553e-17
e_pi_t4.d -6.436822e-18
pi.d      -2.680789e-17
delta_e.d -2.027300e-16

Modelagem

Encontramos cointegração com posto da matriz igual a 3 e, dessa forma, estimamos um modelo VECM usando defasagens definidas por critérios de informação e representamos este modelo em um modelo VAR em nível:


Coefficient matrix of lagged endogenous variables:

A1:
            pi_l.l1        h.l1  e_pi_t4.l1        pi.l1 delta_e.l1
pi_l     0.11359649  0.27648329 -0.04885710  0.152824045 0.35369089
h        0.09670218  1.92995563 -0.11577871 -0.057150208 0.46655568
e_pi_t4  0.01536299  0.02953131  0.05858063 -0.001075209 0.05106807
pi      -0.08599410  0.22082484  0.47869099  0.411764874 0.43878381
delta_e -0.13738973 -0.05444054 -0.15960449  0.050324088 0.38010592


A2:
              pi_l.l2         h.l2  e_pi_t4.l2       pi.l2  delta_e.l2
pi_l    -0.0863798960 -0.393198417 -0.03968366  0.08455109  0.29341342
h        0.0407470234 -1.477829208  0.43938049 -0.63063005 -0.53765115
e_pi_t4 -0.0005530933  0.008831046 -0.02024436 -0.02036030  0.05034806
pi      -0.3483048832 -0.254758642  0.20689618  0.07109025  0.32182343
delta_e  0.1622069015  0.223482451  0.01567441 -0.14534048  0.07018108


A3:
             pi_l.l3        h.l3  e_pi_t4.l3      pi.l3  delta_e.l3
pi_l     0.151278230  0.24039833 -0.11771027 0.38373642  0.15769032
h        0.397916551  0.71400935 -0.04265780 0.03239136  0.22898160
e_pi_t4 -0.008578893 -0.02245598  0.07285092 0.03978171  0.03748562
pi       0.195131424  0.04357508 -0.67397395 0.35730231 -0.05625527
delta_e -0.393850640 -0.19731941  0.31032972 0.30254400  0.25505530


A4:
            pi_l.l4         h.l4   e_pi_t4.l4       pi.l4  delta_e.l4
pi_l    -0.10091363 -0.074553751 -0.549201643  0.05211263  0.01104026
h       -0.19526526 -0.188985596  0.466843520 -0.28494522  0.11763701
e_pi_t4  0.03426022 -0.002609558  0.593247781  0.05197292  0.04396279
pi       0.18710390  0.016303549 -0.239201288 -0.20522475  0.20722677
delta_e  0.21769324  0.016368714  0.004613678  0.00692698 -0.08072448


Coefficient matrix of deterministic regressor(s).

           constant         sd1         sd2          sd3
pi_l     0.40116396  0.34594712  0.42124556  0.192130120
h       -0.02140351 -0.13177088 -0.06531445  0.006733912
e_pi_t4  0.05852802  0.03048884  0.04007619  0.014466184
pi       0.26202832  0.25838184  0.16530165  0.038009354
delta_e -0.08535899 -0.02161966 -0.08057569 -0.020466100

Como pode ser visto, os coeficientes de $\Delta_e$ na equação de $\pi^L$ são todos positivos. De modo a avançar, diagnosticamos a especificação do modelo representado em VAR com os testes de autocorreção, normalidade e heterocedasticidade, conforme resultados abaixo:

# Teste de autocorrelação

    Portmanteau Test (asymptotic)

data:  Residuals of VAR object modelo_var
Chi-squared = 306.63, df = 305, p-value = 0.4629

# Teste de normalidade

Skewness

    Skewness only (multivariate)

data:  Residuals of VAR object modelo_var
Chi-squared = 13.738, df = 5, p-value = 0.01736


$Kurtosis

    Kurtosis only (multivariate)

data:  Residuals of VAR object modelo_var
Chi-squared = 50.445, df = 5, p-value = 1.124e-09

# Teste para heterocedasticidade


    ARCH (multivariate)

data:  Residuals of VAR object modelo_var
Chi-squared = 1080, df = 1125, p-value = 0.8283

Os resíduos do modelo são homocedásticos e não autocorrelacionados, porém não são normalmente distribuídos. As séries temporais apresentam outliers, característico de dados econômicos. Dessa forma, mesmo com transformações e/ou dummies é um desafio atingir a normalidade destas variáveis. Ignoraremos este problema aqui, enfatizando que intervalos de confiança calculados a partir deste modelo podem ser imprecisos.

Análise de impulso resposta

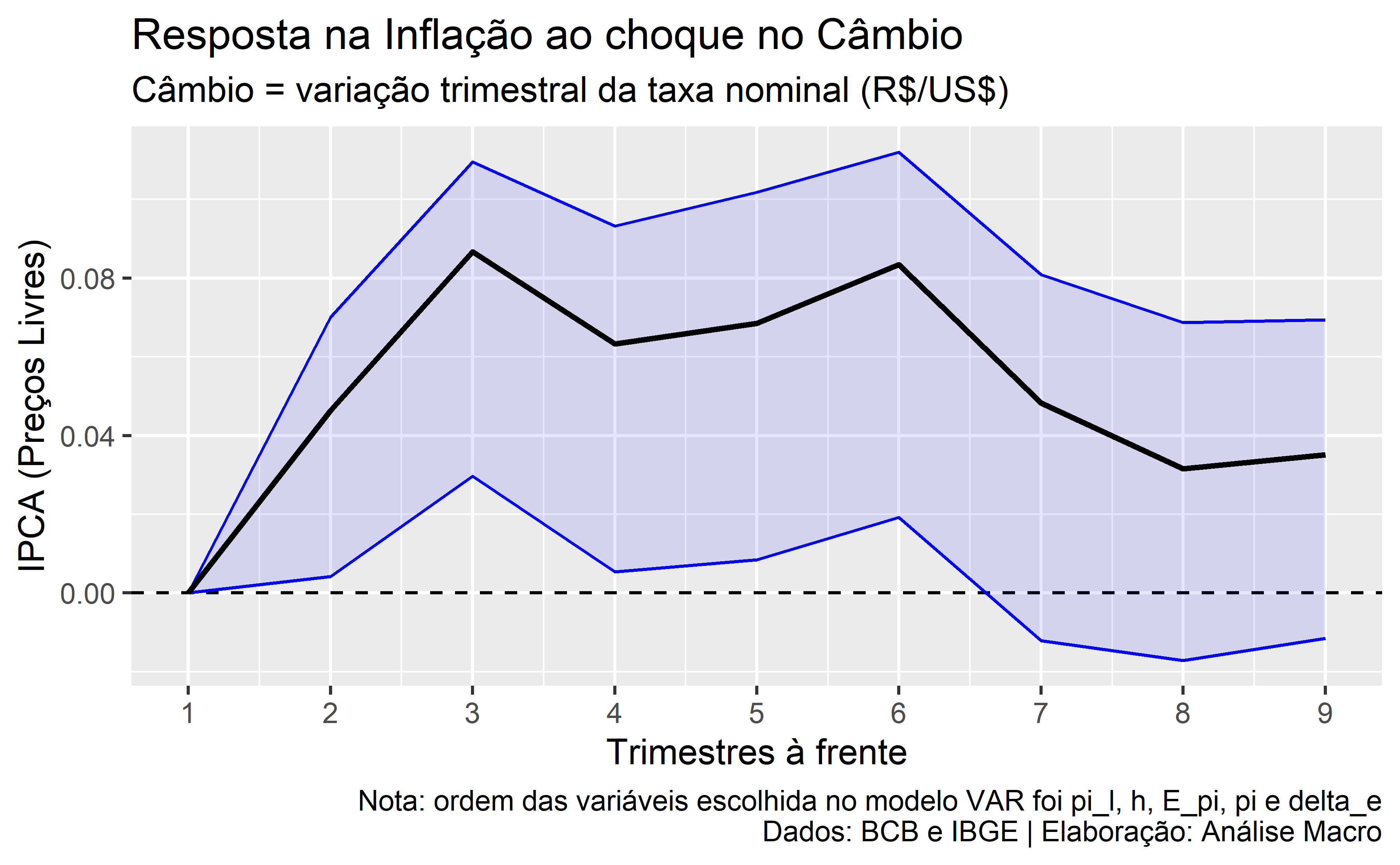
Com este modelo, calculamos as funções impulso resposta dando um choque na variação do câmbio para obter a resposta na inflação de preços livres nos próximos 8 períodos (trimestres). Intervalos de confiança de 95% são gerados usando bootstrapping. O gráfico de resultado é exposto abaixo:

Os principais resultados são os seguintes:

Choques cambiais não são repassados instantaneamente para o nível de preços;
O efeito dos choques cambiais sobre a inflação de preços livres tende a ser positivo;
Um choque de um desvio padrão na variação da taxa de câmbio tem um efeito inicial pequeno, mas persistente ao longo do tempo, ficando não significativo após 7 trimestres;
Considerando intervalos de confiança, o repasse cambial varia de 0,003 p.p até 0,11 p.p. sobre a inflação de preços livres do trimestre em questão;
Em termos acumulados, espera-se um aumento de 0,34 p.p na inflação de preços livres após 6 trimestres do choque inicial na variação da taxa de câmbio.

Conclusão

Referências

BANCO CENTRAL DO BRASIL (2018). Repasse cambial sob a ótica de um modelo semiestrutural. Box do Relatório de Inflação de Setembro de 2018.

Quer aprender mais?

Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise do Censo Demográfico com o R

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Criando um Dashboard de análise de Ações no Python

Analisando séries temporais no Python e esquecendo de vez o Excel

Cálculo do Retorno Econômico de uma Política Pública

Outros artigos relacionados

Análise do Censo Demográfico com o R

Como podemos analisar dados do Censo Demográfico para produzir pesquisas e implementar políticas públicas? Mostramos nesta postagem o resultado de uma breve análise dos dados preliminares do Censo Demográfico de 2022 usando o R.

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Colocar modelos em produção pode ser um grande desafio. Lidar com custos monetários, infraestrutura operacional e complexidades de códigos e ferramentas pode acabar matando potenciais projetos. Uma solução que elimina todos estes obstáculos é a recém lançada Shinylive. Neste artigo mostramos um exemplo com um modelo de previsão para o preço do petróleo Brent.

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Manter relatórios diários com dados e análises atualizados é um desafio, pois envolve várias etapas: coleta de dados, tratamento de informações, produção de análises e atualização de relatório. Para superar este desafio algumas ferramentas como Python + Quarto + GitHub podem ser usadas para automatizar tudo que for automatizável. Neste artigo mostramos um exemplo com dados do mercado financeiro.