Resumo
Este exercício estima o Hiato do Produto do Brasil utilizando quatro métodos univariados distintos. Para lidar com o problema de fim de amostra causado por filtros univariados, incorporamos previsões do PIB provenientes de agentes econômicos e projeções simples, estendendo a série temporal além da amostra original. Todo o processo de coleta, tratamento, estimação e visualização dos hiatos foi realizado na linguagem de programação R.
Introdução
O “problema de fim de amostra” (ou end-of-sample problem, em inglês) surge na extremidade final de uma série temporal, onde a ausência de dados futuros compromete a estimação da tendência e, consequentemente, do hiato do produto — definido como a diferença entre o PIB observado e o PIB potencial. Esse problema afeta métodos que dependem da série completa para estimar componentes como tendência e ciclo, tornando as estimativas menos precisas no final da amostra.
Na última postagem no Clube AM, Investigando o problema de fim de amostra na estimativa do Hiato do Produto usando a linguagem R, comparamos estimativas do hiato do produto em duas situações: (i) utilizando apenas dados disponíveis até o presente (hiato quase em tempo real) e (ii) considerando a amostra completa. Observamos diferenças significativas nos valores estimados ao longo do tempo, evidenciando a necessidade de soluções para mitigar esse problema.
Uma abordagem para contornar essa limitação é a incorporação de previsões do PIB, seja por meio de projeções de agentes de mercado ou de modelos próprios, permitindo a extensão da série além do último ponto disponível. No entanto, essa estratégia adiciona incerteza, pois a qualidade das estimativas do hiato dependerá da precisão dessas previsões.
Neste exercício, utilizamos dados do PIB índice número (base 1995 = 100) ajustado sazonalmente, extraídos da tabela 1621 do SIDRA/IBGE, como base da amostra original. Para expandir a série, incorporamos previsões do Boletim Focus para o PIB até 2026Q3 e, adicionalmente, aplicamos um modelo Damped Holt-Winters para projetar a série do PIB até 2028Q4.
Métodos
Serão utilizados quatro métodos para a estimação do Hiato do Produto:
- Tendência Quadrática
- Tendência Não Paramétrica
- Filtro Hodrick-Prescott (HP)
- Filtro de Hamilton
Para uma explicação detalhada dessas metodologias, consulte: Investigando o problema de fim de amostra na estimativa do Hiato do Produto usando a linguagem R.
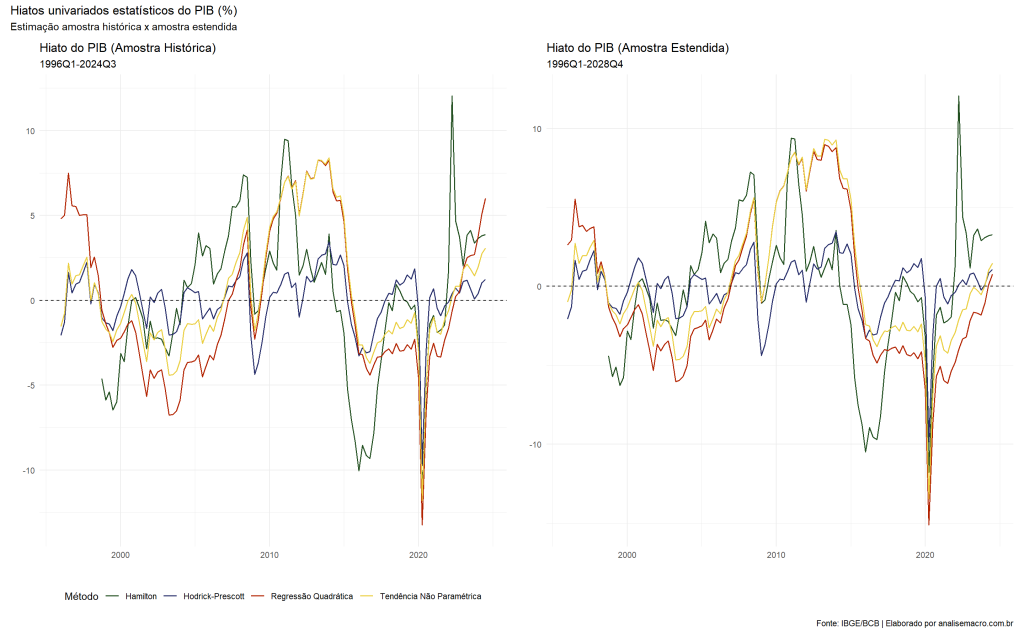
Os resultados demonstram que o comportamento do hiato no fim da amostra varia significativamente entre os dois cenários analisados. No caso da amostra original, observamos oscilações de alta magnitude nos valores estimados. Já com a amostra estendida, os valores tornam-se mais estáveis e próximos de 0%, indicando menor volatilidade na estimativa do Hiato do Produto.
Vale destacar que o Filtro de Hamilton apresentou diferenças menos expressivas entre os dois cenários, como era esperado. Esse método, por construção, busca mitigar o problema de fim de amostra, embora seus resultados ainda possam ser levemente impactados por essa limitação.
Considerações Finais
Com base neste e no exercício anterior, confirmamos a existência do problema de fim de amostra na estimação do Hiato do Produto por meio de filtros univariados e bidirecionais, o que resulta em estimativas menos confiáveis no final da amostra. Além disso, demonstramos como a linguagem R pode ser utilizada para coleta, tratamento, modelagem e análise de dados econômicos, permitindo abordagens mais robustas para lidar com essa limitação.
Referências
BANCO CENTRAL DO BRASIL. Relatório de Inflação, junho de 2024. Brasília: Banco Central do Brasil, 2024. Boxe “Medidas de hiato do produto no Brasil”, p. 10. Disponível em: https://www.bcb.gov.br/content/ri/relatorioinflacao/202406/ri202406b10p.pdf. Acesso em: 24 fev. 2025.
HAMILTON, J.D. Why you should never use the Hodrick-Prescott filter. Review of Economics and Statistics, v. 81, n. 1, p. 1-17, 1999.
HODRICK, R.J.; PRESCOTT, E.C. Postwar U.S. business cycles: An empirical investigation. Journal of Money, Credit, and Banking, v. 29, n. 1, p. 1-16, 1997.