Introdução
O método ideal para avaliação de políticas (e de qualquer aferição de causalidade) é o experimento do tipo RCT (estudo randomizado controlado).
A ideia básica é atribuir aleatoriamente os indivíduos a dois grupos diferentes, um que recebe o tratamento (o grupo de tratamento) e outro que não (o grupo de controle) e comparar os resultados de ambos os grupos para obter uma estimativa da média do efeito de tratamento.
O problema é que RCT são frequentemente difíceis ou mesmo impossíveis de implementar.
No entanto, muitas vezes temos apenas dados observacionais, aqueles que não podemos definir quem será exposto a um tratamento.
Neste caso, o esforço passa sempre por mostrar que o grupo de controle é adequado para representar os resultados potenciais dos indivíduos tratados, caso estes não tivessem sido tratados.
Diferenças-em-Diferenças
Diferenças-em-Diferenças (diff-in-diff) é um modelo simples e eficaz que nos permite olhar para o efeito causal de uma intervenção política em dados observacionais.
Para isso, observamos como a média da variável de interesse se comporta antes e depois do tratamento, comparando com o grupo de controle no mesmo período.
A equação básica do Diff in Diff pode ser representada da seguinte forma:
![\[Y_{it} = \alpha + \beta_1 \text{(Tratamento)}_i + \beta_2 \text{(Pós-Tratamento)}_t + \beta_3 \text{(Tratamento)}_i \times \text{(Pós-Tratamento)}_t + \text{Controles } + \epsilon_{it}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-e57920d98ca9f370dfbb8a92281aba62_l3.png "Rendered by QuickLaTeX.com")
Onde:
- 
é a variável de interesse para a unidade i no período de tempo t.
- 
é uma constante.
- 
é o efeito médio do tratamento.
- 
é o efeito médio do tempo após o tratamento.
- 
é o efeito da interação entre tratamento e tempo após o tratamento.
- 
é uma variável indicadora que é 1 se a unidade i pertence ao grupo de tratamento e 0 caso contrário.
- 
é uma variável indicadora que é 1 se o período de tempo t é após a implementação do tratamento e 0 caso contrário.
- 
refere-se às variáveis de controles que garantem a independência condicional do modelo.
- 
é o termo de erro.
A interpretação do coeficiente é o efeito causal do tratamento sobre a variável de interesse ao longo do tempo após o tratamento, controlando os efeitos fixos do tempo e do tratamento.
Tendências Paralelas
A premissa de tendências paralelas é a mais crítica das hipóteses para garantir a validade interna dos modelos diff-in-diff e é a mais difícil de cumprir.
Exige que, na ausência de tratamento, a diferença entre o grupo tratamento e controle seja constante ao longo do tempo. Ou seja, de que a mudança nos resultados de pré para pós-intervenção no grupo de controle é um bom contrafactual para os resultados potenciais não tratados no grupo de tratamento.
Esta é uma suposição, ou seja, não é algo que possamos testar, porque envolve resultados contrafactuais não observados.
Estudo de Caso: Impacto na redução do ICMS
Porto União (SC) e União da Vitória são chamadas cidades irmãs, pois são divididas apenas pelo limite entre os estados de Santa Catarina e Paraná, o que as torna um município apenas. Entretanto, cada uma tem a própria gestão municipal e, obviamente, segue as políticas do próprio estado.
Quer saber como essa análise foi construída? Seja aluno do nosso curso Avaliação de Políticas Públicas usando Python, e tenha acesso às aulas teóricas e práticas, com o código disponibilizado em Python.
Assim, suponha que em 2015 o estado do Paraná, com o objetivo de melhorar o dinamismo econômico, reduza a alíquota do Imposto sobre Circulação de Mercadorias e Serviços (ICMS). Ou seja, supondo a ausência de spillovers, a política afeta empresas da cidade paranense, mas não da catarinense.
Para avaliarmos o impacto dessa política, dispomos de dados do período de 2010 a 2020 com o lucro anual (em milhares de reais) de várias empresas nos dois municípios. Assim, podemos ver o efeito da alteração da alíquota a partir de 2015.
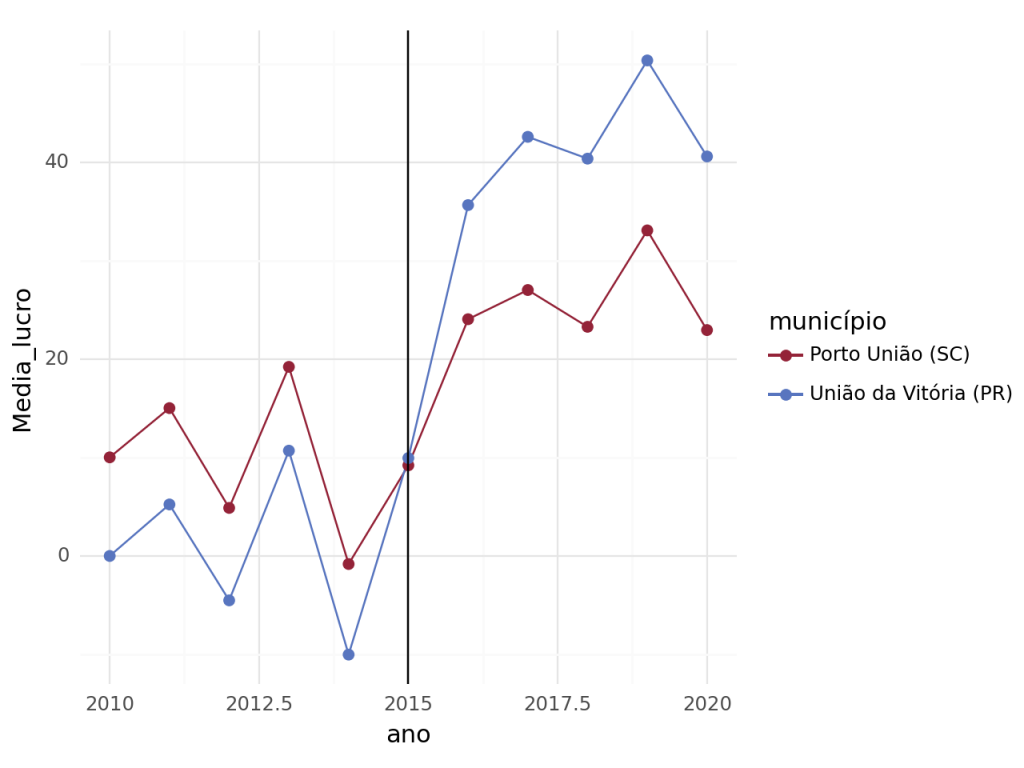
Como temos uma boa série de tempo antes do tratamento ocorrer, é ideal mostrar as tendências como forma de averiguar a plausabilidade da hipótese de tendências comuns entre os dois grupos. Para isso, calculamos a média por grupo e ano e colocamos em um gráfico.
Como as tendências antes do tratamento são paralelas, temos um bom argumento para validar a hipótese. Com isso, podemos estimar o impacto da política com uma regressão. Dado que nós temos mais de dois períodos, temos que estimar com uma variável binária em relação ao ano.
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept 9.6760 0.835 11.589 0.000 8.039 11.313
C(ano)[T.2011] 5.2171 1.089 4.792 0.000 3.083 7.351
C(ano)[T.2012] -4.7696 1.086 -4.391 0.000 -6.899 -2.640
C(ano)[T.2013] 10.1788 1.114 9.138 0.000 7.995 12.362
C(ano)[T.2014] -10.3444 1.089 -9.496 0.000 -12.480 -8.209
C(ano)[T.2015] -3.172e+13 3.18e+13 -0.999 0.318 -9.4e+13 3.06e+13
C(ano)[T.2016] -3.172e+13 3.18e+13 -0.999 0.318 -9.4e+13 3.06e+13
C(ano)[T.2017] -3.172e+13 3.18e+13 -0.999 0.318 -9.4e+13 3.06e+13
C(ano)[T.2018] -3.172e+13 3.18e+13 -0.999 0.318 -9.4e+13 3.06e+13
C(ano)[T.2019] -3.172e+13 3.18e+13 -0.999 0.318 -9.4e+13 3.06e+13
C(ano)[T.2020] -3.172e+13 3.18e+13 -0.999 0.318 -9.4e+13 3.06e+13
tratamento -9.3808 0.686 -13.673 0.000 -10.726 -8.036
pos 3.172e+13 3.18e+13 0.999 0.318 -3.06e+13 9.4e+13
tratamento:pos 22.7081 0.929 24.446 0.000 20.887 24.529
==================================================================================Nosso parâmetro de interesse é o “tratamento:pos”. Portanto, podemos ver que a diminuição da alíquota de ICMS aumentou o lucro das empresas de União da Vitória em 22 mil reais.
