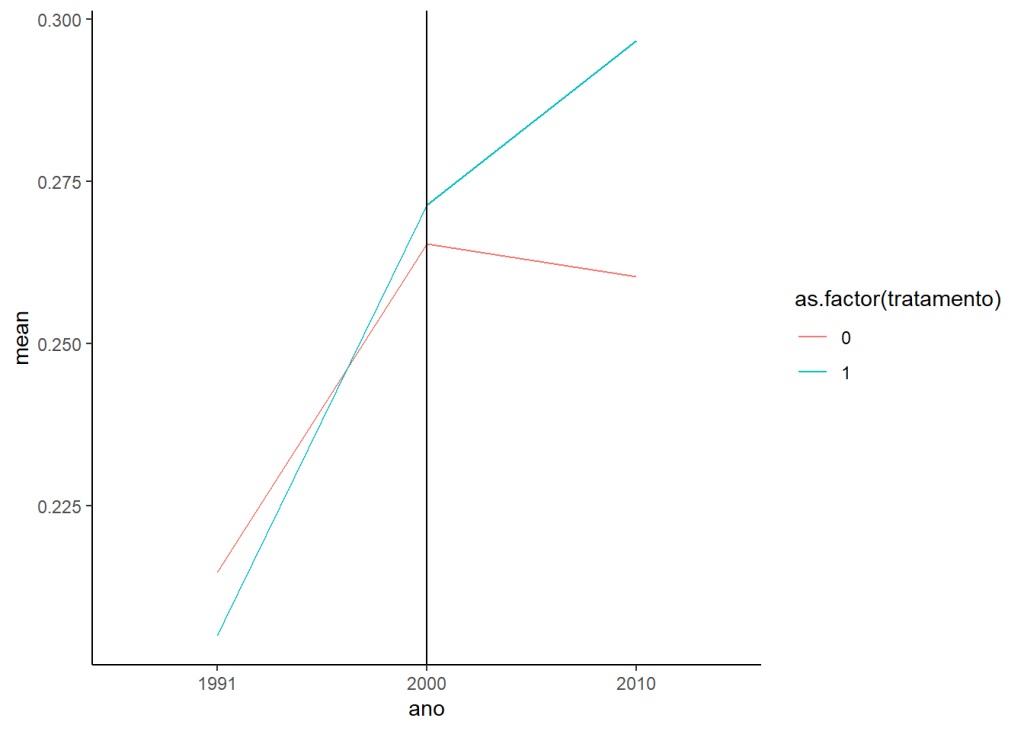
O escore de propensão é provavelmente a maneira mais comum de agregar múltiplas variáveis de correspondência em um único valor que pode ser correspondido, ou seja, muito útil para a realização de pareamento.
O escore de propensão é a probabilidade estimada de que uma determinada observação teria sido tratada. A correspondência de escore de propensão muitas vezes significa selecionar um conjunto de observações de controle correspondidas com valores semelhantes do escore de propensão.
Como exemplo para mostrar o poder dos métodos de pareamento utilizaremos o caso do impacto econômico do metrô de São Paulo. O transporte pode ter grande impacto nos aspectos econômicos de uma localidade, pois permite e expande o acesso das pessoas aos empregos, promove a eficiência e fomenta economias de aglomeração. Assim, estimaremos o impacto da construção de estações de metrô na verticalização, medida pela proporção de domicílios que são apartamentos, dos domicílios próximos a elas. Mais especificamente, analisaremos o impacto das estações de metrô construídas em São Paulo entre 2002 e 2007, das linhas verdes e lilás.
Seja aluno da nossa formação Do Zero à Avaliação Prática de Política Públicas com a Linguagem R, e tenha acesso às aulas teóricas e práticas, com o código disponibilizado em R .
Utilizaremos dados dos censos de 1991, 2000 e 2010 com algumas variáveis em nível de setor censitário para a cidade de São Paulo. Para fins de definição dos setores censitários tratados, ou seja, que sofreram a intervenção da política pública, estamos considerando a distância de até 1km até a estação construída mais próxima. No mapa a seguir, mostramos como era a renda per capita dos setores censitários de São Paulo em 1991. Os números estão deflacionados e constantes para valores de 2010.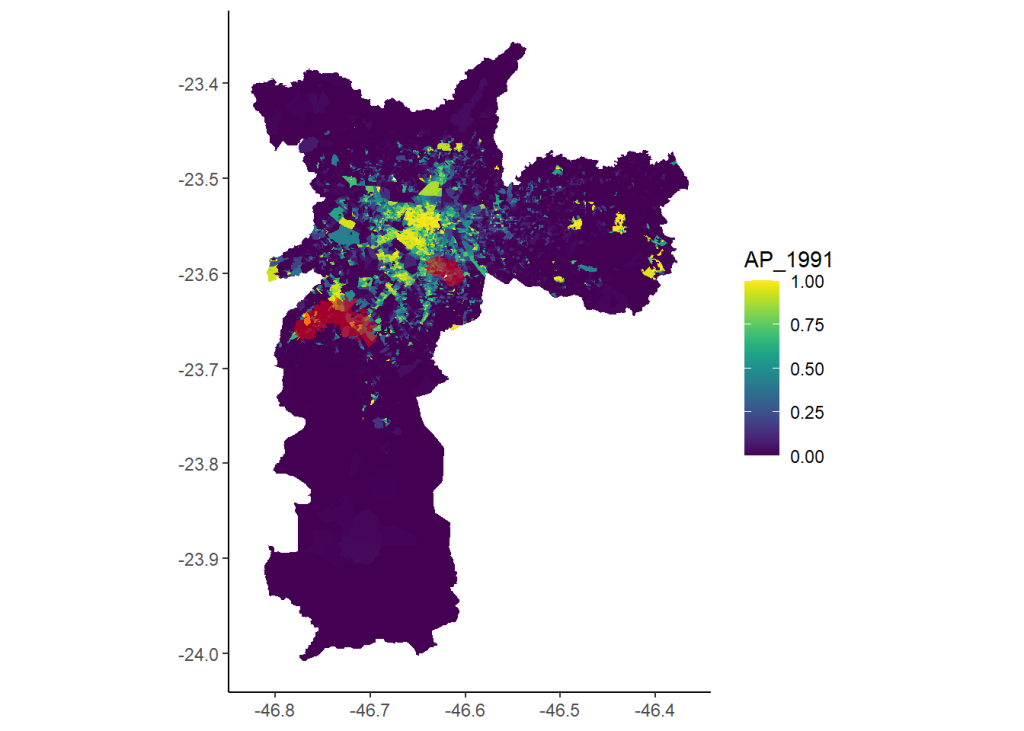
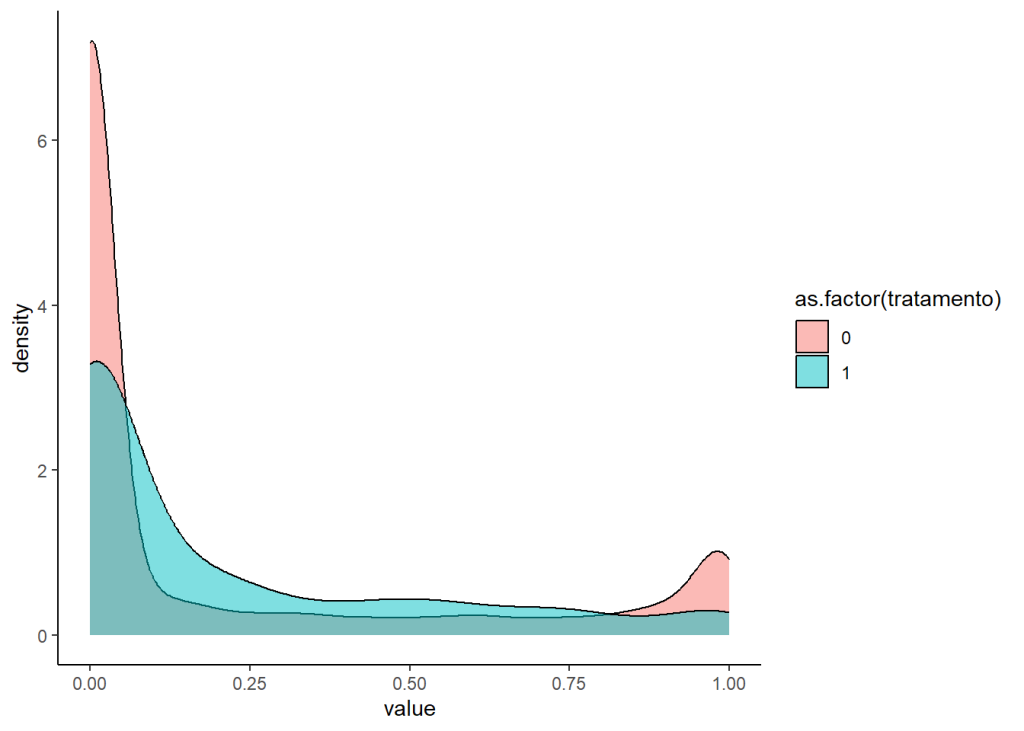
Quando comparamos a distribuição da verticalização entre estes dois grupos (tratados (1) e restantes (0)) isso fica mais claro.
Veja que se formos estimar o modelo de diferenças-em-diferenças, nós precisamos adequar o grupo de controle para que as tendências fiquem paralelas.
Assim, para avaliar o efeito, é preciso tornar esses grupos semelhantes. Para isso, utilizaremos o pareamento, que permite selecionar setores de dentro do grupo restante para formar um grupo de controle parecido com o grupo de tratamento.
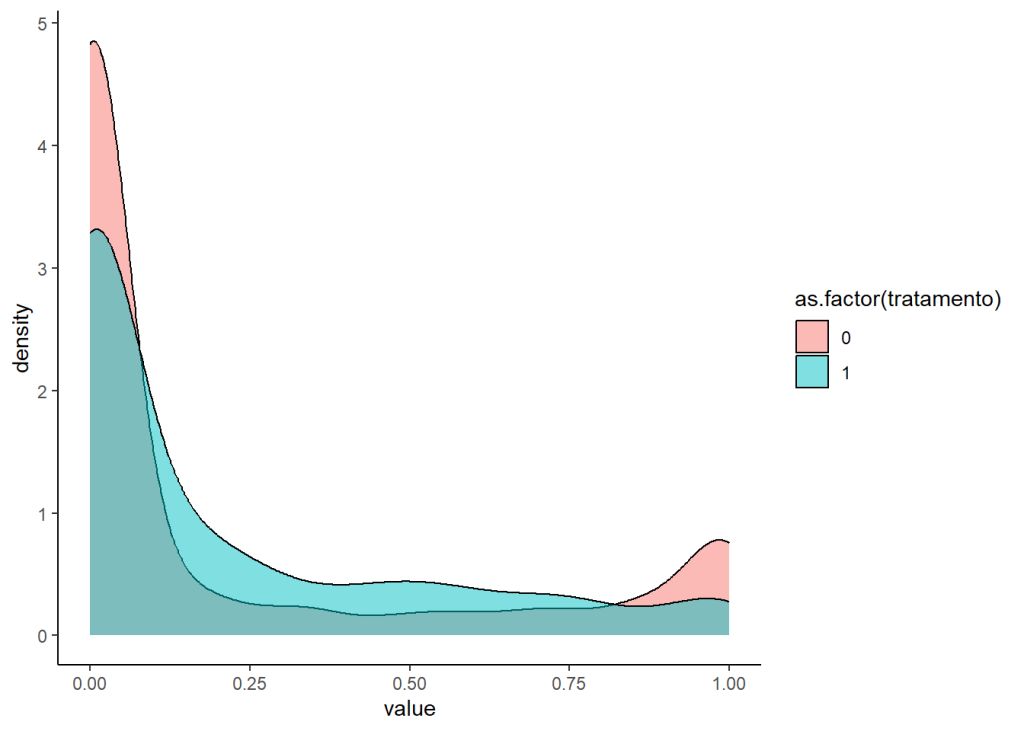
Além da variável de verticalização, também utilizamos a renda domiciliar per capita, a proporção de pessoas com ensino superior, a proporção de domicílios que são alugados e a proporção de jovens adultos (25-34 anos) entre os moradores do setor censitário. O resultado mostra que a distruibuição do grupo de controle fica mais próxima a distribuição que ocorre nos setores tratados.
Além disso, até aqui estamos tratando apenas da variável de interesse. Ainda não podemos afirmar que o equilíbrio dos dois grupos está adequado.
| Type | Diff.Un | Diff.Adj | M.Threshold | |
|---|---|---|---|---|
| distance | Distance | 0.1748641 | -0.0001736 | Balanced, <0.1 |
| RPC_1991 | Contin. | 0.0850701 | -0.0077821 | Balanced, <0.1 |
| AP_1991 | Contin. | -0.0332663 | -0.0126687 | Balanced, <0.1 |
| grad_1991 | Contin. | 0.0849201 | 0.0265063 | Balanced, <0.1 |
| Rent_1991 | Contin. | 0.0291053 | 0.0017758 | Balanced, <0.1 |
| youngadults_1991 | Contin. | 0.0062660 | -0.0895888 | Balanced, <0.1 |
| Single_1991 | Contin. | 0.1389738 | -0.0342860 | Balanced, <0.1 |
Veja que, utilizando o critério de até 0.1 desvio padrão de tolerância, há um bom balanceamento entre os grupos em todas as variáveis.
Podemos utilizar o método “ótimo” para testar se podemos melhorar ainda mais o equilíbrio.
O uso desse método piorou bastante os resultados. Dado os bons resultados, podemos voltar para o método padrão de vizinhos mais próximos. Veja que, apesar das médias estarem equilibradas, a distribuição da nossa variável de interesse ainda está um pouco longe do ideal. A depender do objetivo de análise, pode ser interessante testar outras possibilidades para tentar melhorar esse fator.
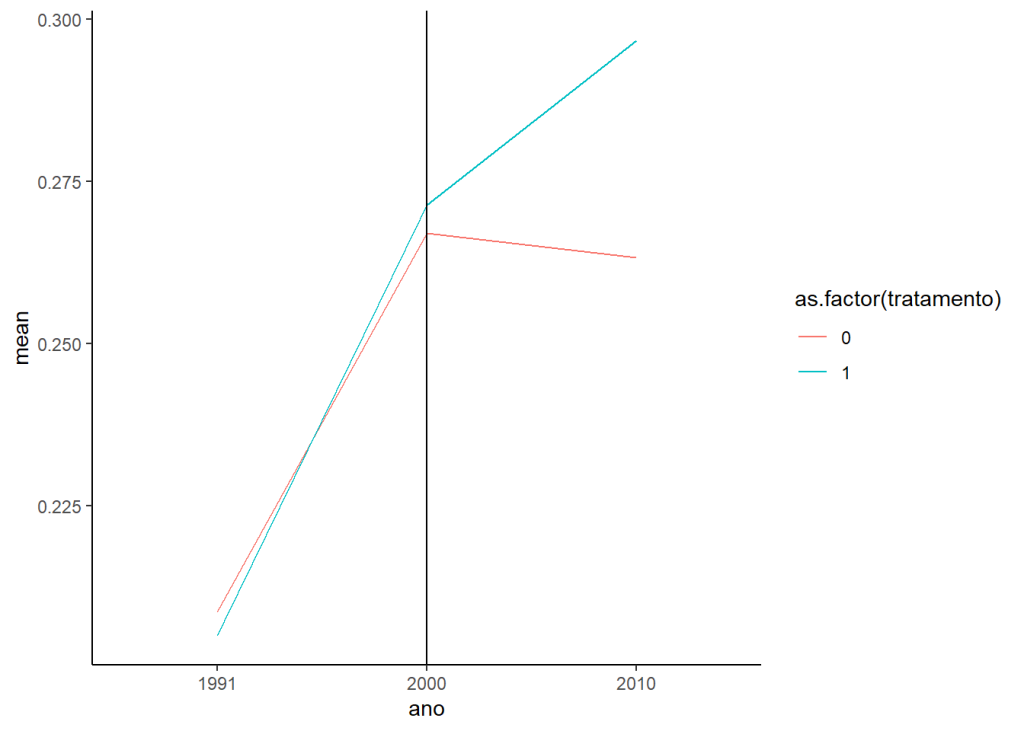
Assim, podemos mostrar o poder do pareamento com um gráfico das diferenças médias padronizadas absolutas entre os grupos de tratamento e controle, antes (azul) e depois (vermelho) do pareamento. Veja que não havia um severo desbalanceamento entre as variáveis antes, mas ele melhorou significativamente. Entretanto, a variável que mede a proporção de jovens adultos teve uma piora, mas está ainda dentro do limite nós impusemos.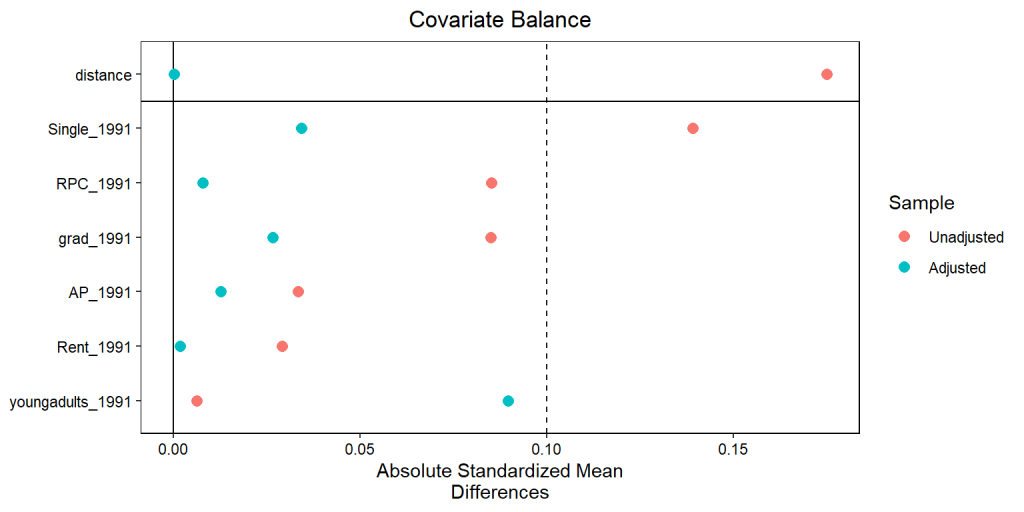
Portanto, podemos ver se o pareamento corrigiu as tendências dos grupos no momento anterior ao tratamento, tornando possível a utilização do modelo de diferenças-em-diferenças.
