Diversos métodos econométricos têm como principal finalidade melhorar o processo de investigar o efeito de uma variável sobre a outra, e um importante método encontra-se no uso de Regressão Descontínua na análise de regressão linear. Mas como podemos utilizar essa ferramenta para auxiliar no estudo da avaliação de impacto?
Neste post, oferecemos uma breve introdução a esse importante método da área de inferência causal, acompanhado de um estudo de caso para uma compreensão mais aprofundada de sua aplicação. Os resultados foram obtidos por meio da implementação em Python, como parte integrante do nosso curso sobre Avaliação de Políticas Públicas utilizando esta linguagem de programação.
Regressão Descontínua
Regressão descontínua (RDD) é um método que estima o efeito da política em casos que o tratamento é definido com base em um linha de corte em uma variável, chamada variável de atribuição. Assim, sendo X a variável de atribuição, T, o tratamento e C, a linha de corte:
(1)
Para deixar mais claro, imagine uma política de transferência de renda em que todas as pessoas que ganham abaixo de 500 reais são elegíveis para o programa. Neste caso, a variável de atribuição é o rendimento e a linha de corte é 500 reais.
A lógica dos desenhos de regressão descontínua é explorar essa linha de corte pra simular um processo de aleatorização. Para isso, a premissa básica é de que indivíduos logo acima e logo abaixo da linha corte são extremamente semelhantes e só estão de um grupo ou no outro por motivos aleatórios.
Pensando nos termos do modelo de resultados potenciais, o que aconteceu com os indivíduos logo acima da linha é uma boa medida para o que aconteceria se aqueles abaixo da linha tivessem sido alvos da política. Assim, esses indivíduos próximos a linha são utilizados para medir o efeito causal do programa.
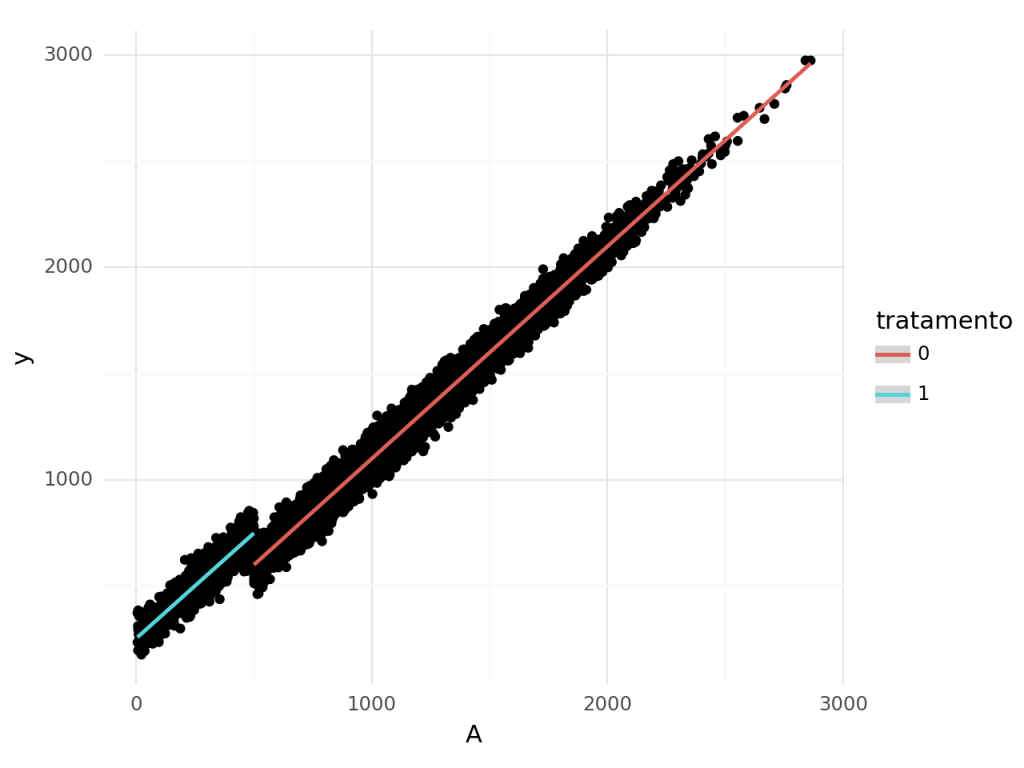
Suponha a existência do programa de transferência de renda mencionado acima. Sendo A, a renda no momento anterior a política e a variável de atribuição. Já Y é a renda no momento posterior ao programa. Assim, podemos que há uma clara quebra ao longo da linha de corte de 500 reais.
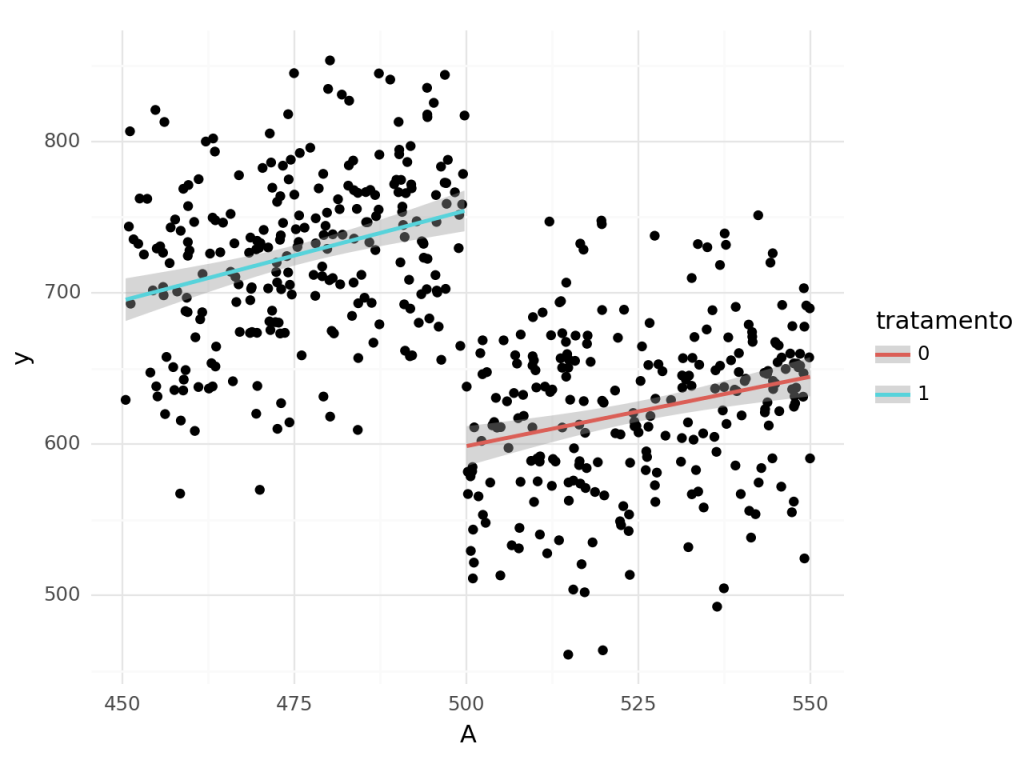
Observando apenas os pontos mais próximos do limite.
Essa aproximação levanta uma questão bastante relevante na hora de realizar estimações com regressão descontínua que é a seleção da proximidade à linha de corte. Há um trade-off nessa escolha. Quanto mais próximos do limite, mais próximos da quebra e, portanto, mais próximos do efeito real. Entretanto, teremos menos dados e, portanto, maior variância.
Primeiramente, é preciso centralizar a variável A, ou seja, diminuir seus valores pelo valor da linha de corte. Para estimarmos o RDD, o jeito mais simples para é rodarmos um OLS com a seguinte especificação:
(2)
Sendo L uma variável binária que assume valor 1 quando A > C e 0, caso contrário. Veja que isso é equivalente a estimar duas regressões, uma a esquerda de C e uma a direita de C. Nosso parâmetro de interesse é o , que mede o efeito direto da política. Se quisermos o valor percentual, é só utilizarmos
Entretanto, para que a diferença na média da variável de interesse entre os grupos seja o efeito da política, é necessário que qualquer fator relevante que possa afetar o Y tenha uma transição suave (seja contínuo) na linha de corte. Por exemplo, se houvesse uma descontinuidade em uma característica importante, como educação, ao longo dos 500 reais, o estimador sofreria de viés de seleção.
Também é necessário que não haja possibilidade do participante controlar a variável de atribuição para definir seu grupo. No caso da política de renda isso pode ser um fator relevante, já que a pessoa pode escolher ganhar menos ou ocultar rendimentos para participar do programa.
Qual o efeito do consumo de álcool na mortalidade usando a idade mínima para beber como limite?
Um bom exemplo de uso da de regressão descontínua é o artigo de Carpenter e Dobkin (2009), que estimam o efeito do consumo de álcool na mortalidade usando a idade mínima para beber como limite no RDD.
Quer saber como essa análise foi construída? Seja aluno do nosso curso Avaliação de Políticas Públicas usando Python, e tenha acesso às aulas teóricas e práticas, com o código disponibilizado em Python.
Essa é uma questão importante em termos de pesquisa, dado que diferentes países utilizam diferentes idades e isso pode ter impacto significativo em diversos fatores. Nos Estados Unidos, país do estudo, a idade mínima é 21, 3 anos maior do que a maior parte do resto do mundo.
Utilizando os dados do trabalho, iremos estimar o efeito desse limite na mortalidade por diversos fatores. Os dados já estão agregados por mês de nascimento. Portanto, representam a média dos valores por idade em anos-meses.
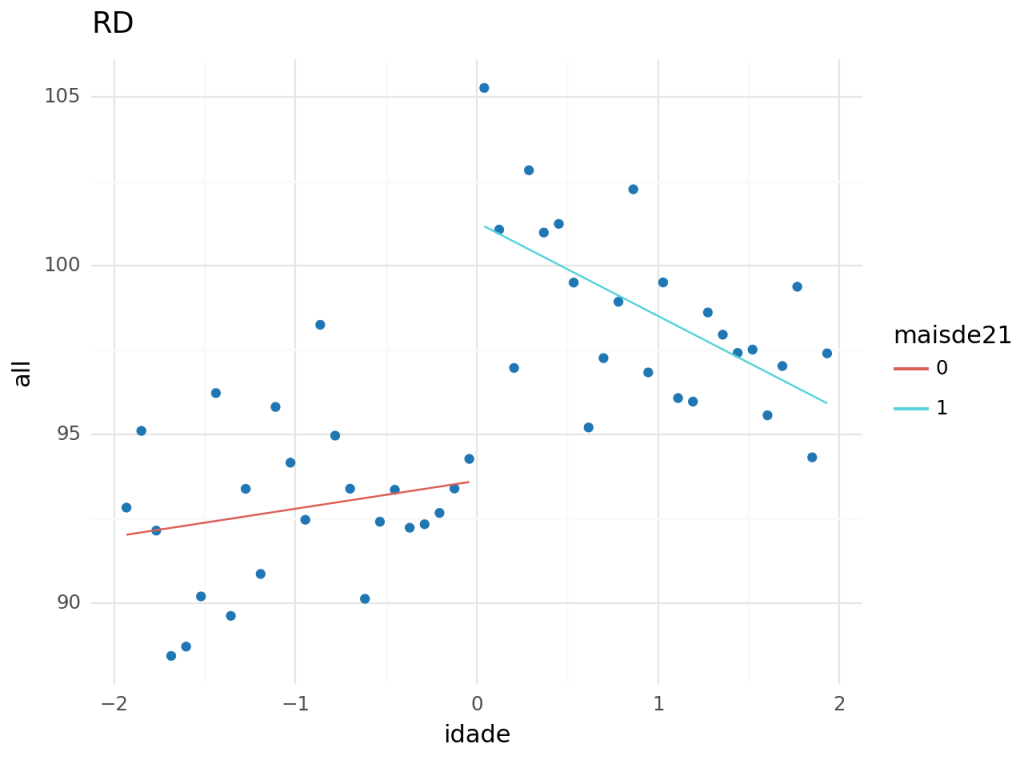
Podemos fazer a inspeção visual para avaliar a relação das causas de morte com a idade. É possível perceber que há uma descontinuidade muito clara em algumas variáveis e em outras não há nenhuma aparente. Chama atenção as mortes relacionadas diretamente ao consumo de álcool, que aumentam significativamente no primeiro mês pós aniversário de 21 anos, mas depois volta para a tendência anterior.
Assim, estimaremos a regressão descontínua para as variáveis com quebras mais aparentes na linha de corte. São elas: Todas as causas, relacionadas ao consumo de álcool, acidentes de transito e suicídio.
Para estimarmos, realizamos o procedimento de interagir uma dummy, que reflete a unidade estar ou não acima da linha de corte com a variável de idade.
Aqui, o intercepto é o parâmetro da regressão abaixo da linha de corte. Já
é o intercepto para a regressão acima da linha de corte.
Os resultados mostram que o consumo de álcool aumenta as chance de morte para todas as causas em 8% (100*((7.6627+93.6184)/93.6184 - 1).
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | 93.6184 | 0.932 | 100.399 | 0.000 | 91.739 | 95.498 |
| idade | 0.8270 | 0.819 | 1.010 | 0.318 | -0.823 | 2.477 |
| threshold | 7.6627 | 1.319 | 5.811 | 0.000 | 5.005 | 10.320 |
| idade:threshold | -3.6034 | 1.158 | -3.111 | 0.003 | -5.937 | -1.269 |
 Referências
Referências
Facure, Matheus. 2022. Causal Inference for The Brave and True. https://matheusfacure.github.io/python-causality-handbook/landing-page.html.