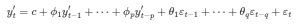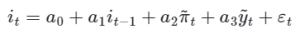A taxa de juros básica é uma variável macroeconômica fundamental para entender a economia de um país, além de servir de referência para diversas outras taxas. No Brasil essa taxa é conhecida como Selic e é definida em reuniões periódicas da autoridade monetária, o Banco Central. Nestas reuniões um comitê analisa a situação e as perspectivas para a economia, com um amplo conjunto de indicadores e modelos macroeconômicos, e decide sobre o valor da Selic com objetivo de que a inflação fique em linha com a meta definida pelo CMN. Além disso, a taxa Selic é conhecidamente o principal instrumento de política monetária e a única taxa sob controle do BCB.
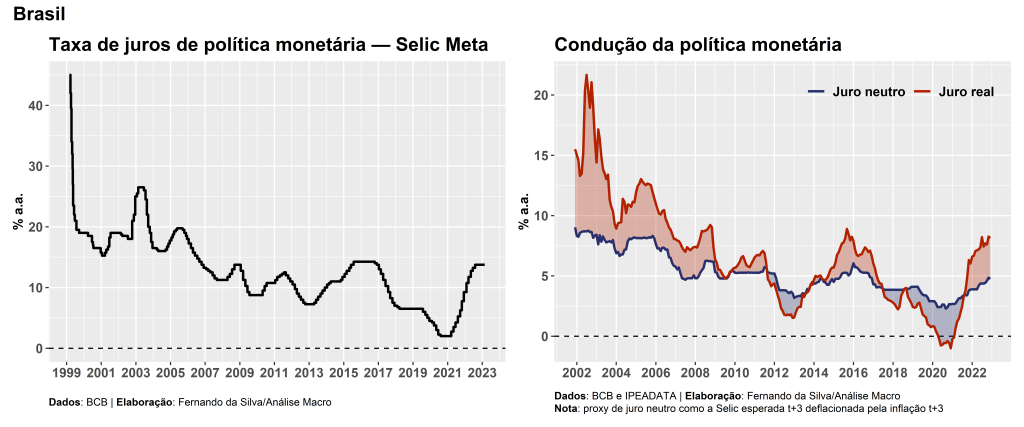
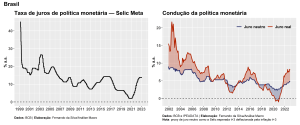
A evolução da taxa de juros básica, a Selic, e a condução da política monetária é exibida nos gráficos abaixo:
Portanto, podemos tirar de conclusão que a Selic possivelmente influencia e é influenciada por diversas variáveis macroeconômicas, observáveis ou não. Reconhecer isso é importante para um exercício de previsão, que é o objetivo deste artigo. Com isso dito, como poderíamos elaborar previsões para a taxa Selic? A seguir exploramos resumidamente algumas possibilidades e abordagens, focando no aspecto prático de implementação e de comparação da acurácia dentre as opções.
Abordagem 1: modelos simples
A abordagem mais simples para previsão da taxa de juros básica, a Selic, é ignorar tudo que está escrito nos 4 parágrafos anteriores e utilizar modelos univariados de séries temporais. Dentro dessa classe, os principais modelos simples que podem ser explorados são os da família ARIMA.
Por sua simplicidade, não podemos esperar resultados muito interessantes destes modelos, dado que eles exploram, basicamente, os valores passados da série temporal para previsão de valores futuros. Na economia nem sempre o passado é útil para explicar ou prever o futuro. A forma geral destes modelos é essa:
Aqui y′ é a série temporal estacionária (em nível ou nas diferenças), c é uma constante (intercepto) do modelo, ε é o erro defasado e os demais termos são parâmetros a serem estimados.
Abordagem 2: cenários estatísticos
Uma abordagem mais interessante é explorar uma lei de movimento para a variável de interesse e gerar distribuições estatísticas para os termos da equação, de forma a obter múltiplos cenários para a variável de interesse.
Por exemplo, suponha que A segue a lei de movimento tal que A=B/C. Com essa definição de equação em mãos podemos gerar distribuições para B e C, combinar todas as possibilidades e, então, simular valores para A com base em sua lei de movimento.
A vantagem dessa abordagem é que não precisamos estimar parâmetros, nem empregar qualquer método econométrico, e o resultado final não é apenas uma “previsão” pontual, mas sim toda uma distribuição. Além disso, é possível calibrar a distribuição de cada termo de forma a refletir um cenário esperado.
Quanto a lei de movimento para a Selic, o usual seria utilizar alguma especificação da regra de Taylor, que é uma regra de política macroeconômica onde a taxa de juros é determinada exogenamente. Por exemplo, Barbosa et al. (2016) citam uma especificação como essa:
Essa é a especificação econométrica para estimativa da regra de Taylor (não a original) que contém 3 variáveis: a própria taxa de juros defasada, o hiato de inflação e o hiato do produto, além de uma constante. Partindo dessa especificação poderíamos assumir ou simular valores para os parâmetros e gerar distribuições para os demais termos, conforme mencionado, de forma a não precisar empregar algum método de estimação. Essa é uma abordagem simples mas poderosa, pois nem sempre a econometria é empregável ou “harmônica” com os dados observados.
Abordagem 3: modelos macroeconômicos
Por fim, uma abordagem (talvez) mais robusta é o uso de modelos macroeconômicos onde busca-se descrever o comportamento agregado da economia com diversas equações. A economia pode ser descrita de maneira estrutural ou semiestrutural e as variáveis são usualmente determinadas simultaneamente, o que é um desafio em termos de métodos de estimação.
As equações básicas e quase sempre presentes nestes modelos são 4 e aqui apresentamos um resumo da primeira versão, descrita em Bogdanski et al. (2000), para a economia brasileira após o regime de metas:
- Curva IS: é uma curva de demanda agregada da economia, descrevendo o equilíbrio no mercado de bens e serviços. Expressa o hiato do produto em função de suas próprias defasagens, da taxa real de juros e do resultado primário.
- Curva de Phillips: é uma curva de oferta agregada da economia, descrevendo a relação entre a inflação e uma medida de aquecimento da economia (hiato do produto). Expressa a taxa de inflação em função de suas próprias defasagens e/ou expectativas futuras, do hiato do produto, de uma medida de inflação externa mais a taxa de câmbio.
- Regra de Taylor: é uma regra de taxa de juros, descrevendo as decisões de política monetária. Expressa a taxa básica de juros como uma combinação linear de suas próprias defasagens, do desvio da inflação em relação a sua meta e do hiato do produto.
- Condição de paridade de juros descoberta: é uma equação que relaciona o diferencial entre as taxas de juros externas e domésticas com a taxa esperada de desvalorização da moeda doméstica e o prêmio de risco.
Exercício de previsão
Colocando em prática estas possíveis abordagens para previsão da Selic, qual alternativa é a melhor? Como de costume em economia, depende. O foco deste exercício é o aspecto prático de implementação e de comparação da acurácia dentre as opções disponíveis, portanto, logo de cara descartamos a abordagem 3, pelos desafios de estimação e pela brevidade do exercício.
Levando adiante as duas primeiras abordagens, vamos em busca dos dados necessários. A tabela abaixo resume os principais metadados:
| Variável | Descrição | Fonte |
|---|---|---|
| Taxa Selic | Meta Selic definida pelo Copom (% a.a.) | SGS/BCB |
| Hiato da inflação | Desvio da expectativa do IPCA um ano à frente em relação a meta no mesmo horizonte | Focus/BCB e CMN |
| Hiato do produto | Estimativa do Banco Central em seu modelo bayesiano | RI/BCB |
Após definir os dados passamos para a implementação prática das duas primeiras abordagens. O primeiro passo é definir alguns parâmetros para o exercício de previsão. A ideia é fazer um exercício simples buscando investigar qual abordagem entrega resultados relativamente melhores em termos de acurácia. Dessa forma, dividimos a amostra de dados em duas, deixando os últimos 8 trimestres de dados disponíveis para testar as abordagens em termos de previsão pontual versus valor observado.
Na abordagem 1, de modelos simples, vamos utilizar um modelo auto ARIMA para a taxa Selic.
Na abordagem 2, de cenários estatísticos, primeiro precisamos escolher os valores para os termos a da lei de movimento (regra de Taylor) para taxa Selic. Utilizamos estes valores, com base em exercícios anteriores e ao que se encontra na literatura:
a0 = 4,5
a1 = 0,2
a2 = 1,5
a3 = -0,2
Em seguida geramos as distribuições normais assimétricas para i, π (til) e y (til), de maneira a refletir a leitura do autor para as perspectivas da economia no período da amostra de teste (os dados desse período já são conhecidos, mas aqui simulamos o que seria feito em um exercício de previsão quando ainda não conhecemos os dados futuros da variáveis “exógenas”, ou seja, consideramos somente as informações disponíveis para os agentes até um dia antes ao começo do horizonte de previsão). As distribuições são geradas para cada período do horizonte de previsão de interesse, nesse caso 8 trimestres, mas simplificamos gerando uma previsão para cada ano encerrado adiante. Ao final, calculamos a taxa Selic pela sua lei de movimento e consideramos a média da distribuição para cada período como valor de comparação com a outra abordagem.
As previsões pontuais por ambas as abordagens e pela mediana do Focus/BCB (na última compilação estatística antes do horizonte de previsão), comparadas com os valores observados da taxa Selic para os horizontes de previsão (fim de período), são expostas na tabela abaixo:
| Ano | Selic | Abordagem 1 | Abordagem 2 | Focus |
|---|---|---|---|---|
| 2021 | 9.25 | 1.462492 | 4.173237 | 3.0 |
| 2022 | 13.75 | 1.430895 | 6.436472 | 4.5 |
É visível que a Selic, assim como outras variáveis macroeconômicas, dão um “baile” nas previsões de mercado e nas abordagens aqui discutidas. Em outras palavras, economistas e agentes de mercado que trabalham com previsão estão sempre tentando errar menos, mas dificilmente irão acertar os movimentos da taxa básica de juros no médio/longo prazo. A vida não é fácil!
Também é visível que a abordagem 2, de cenários estatísticos, se destacou em relação às demais, errando menos que a abordagem 1 e que as previsões do Focus ao ficar menos distante dos dados observados da Selic. Isso pode ser observado de outras formas também, como pelas métricas de acurácia tradicionais:
| Métrica | Abordagem 1 | Abordagem 2 | Focus |
|---|---|---|---|
| Erro Médio | 10.05331 | 6.195145 | 7.750000 |
| Erro Quadrático Médio | 106.20281 | 39.630606 | 62.312500 |
| Raiz do Erro Quadrático Médio | 10.30547 | 6.295284 | 7.893827 |
| Erro Médio Absoluto | 10.05331 | 6.195145 | 7.750000 |
| Erro Percentual Médio | 86.89138 | 54.036610 | 67.420147 |
Estes resultados são interessantes e, com certeza, podem ser melhorados com mais aprofundamento e estudos. Alguns próximos passos poderia ser o teste de alterações na lei de movimento da Selic, parâmetros diferentes e comparação com outras abordagens, como a de modelos macroeconômicos.
Para implementar este exercício de previsão, passando pelos procedimentos de coleta, tratamento, modelagem/estatística e visualização de dados, utilizamos a linguagem R. Para reprodução de resultados utilizamos a semente 1984.
Saiba mais
Códigos de reprodução em R deste exercício estão disponíveis para membros do Clube AM da Análise Macro.
Para se aprofundar no assunto confira os cursos aplicados de R e Python da Análise Macro:
- Trilha de Macroeconomia Aplicada: https://conteudosam.com.br/pacotes/macroeconomia-aplicada/
- Trilha de Machine Learning e Econometria: https://conteudosam.com.br/pacotes/econometria-e-machine-learning/
- Modelos Preditivos: https://analisemacro.com.br/curso/modelos-preditivos-de-machine-learning/
- Econometria: https://analisemacro.com.br/cursos/econometria/introducao-a-econometria/
- Análise de Séries Temporais: https://conteudosam.com.br/cursos/analise-de-series-temporais/
Referências
Barbosa, F. D. H., Camêlo, F. D., & João, I. C. (2016). A taxa de juros natural e a regra de Taylor no Brasil: 2003-2015. Revista Brasileira de Economia, 70, 399-417.
Bogdanski, J., Tombini, A. A., & Werlang, S. R. D. C. (2000). Implementing inflation targeting in Brazil. Werlang, Sergio R., Implementing Inflation Targeting in Brazil (July 2000). Banco Central do Brasil Working Paper, (1).