Infelizmente não possuímos uma bola de cristal de forma que possamos prever o futuro, e por isso, sempre há uma incerteza em relação a um resultado. Entretanto, apesar de ser extremamente difícil ter 100% de certeza, podemos quantificar essa incerteza, e pelo menos, haver a possibilidade de acertar um certo nível de um resultado. No post de hoje explicamos o que é probabilidade e o seu papel na Análise de Dados.
Antes de introduzir o conceito da probabilidade, devemos entender o conceito de aleatoriedade. A grosso modo, algo é aleatório quando sabemos que haverá um resultado, porém, não sabemos qual será o valor deste resultado, ou seja, segue uma distribuição de probabilidade e não um valor determinístico.
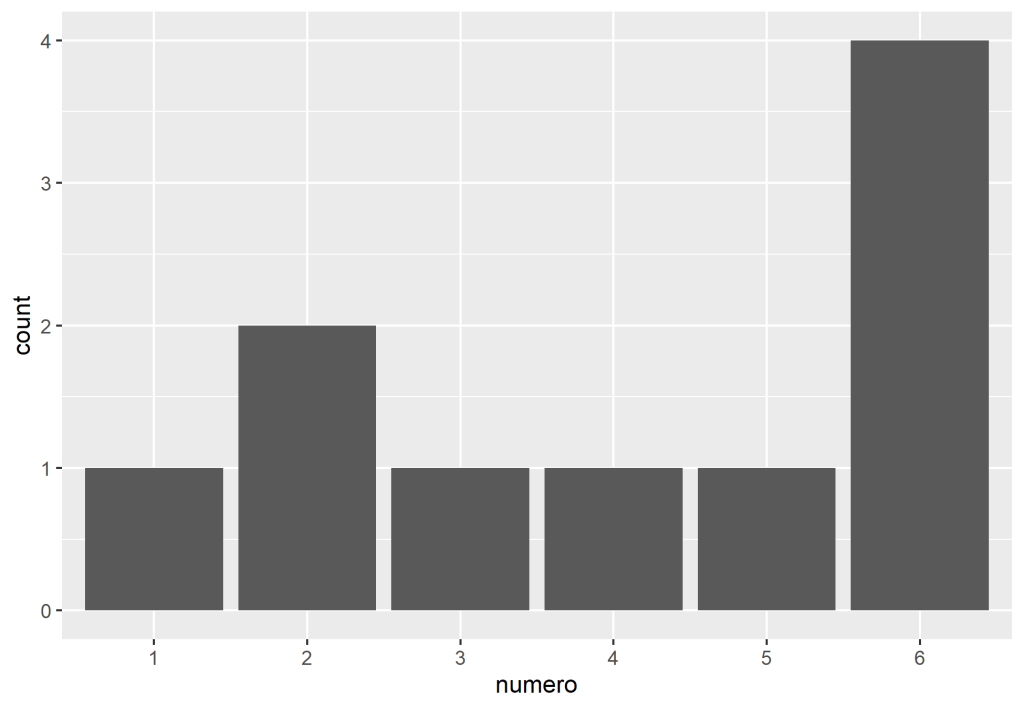
Podemos utilizar o velho exemplo dos dados de seis lados. Se jogarmos o dado, saberemos que o resultado será entre um a seis, porém, não sabemos qual será o seu valor. Essas possibilidade de resultados do dado (um a seis) é chamado de Espaço Amostral. Cada lado desse dado representa uma fração da possibilidade do resultado, sendo sua soma igual a 1 (100%).
Se a probabilidade depende do número de casos favoráveis de cair um lado do dado e do número do casos possíveis, então podemos definir pela equação da probabilidade teórica.
No caso do dado, qual a probabilidade de cair no número dois? Obviamente 1/6.
Construímos um tibble com os valores do dado, e "jogamos" ele com a função sample_n
A função set.seed permite que possamos obter o mesmo resultado sempre. Útil para reprodutibilidade e comunicação dos resultados.
E se estivermos jogando um jogo em que não possamos tirar o mesmo lado novamente? Devemos então levar em conta a amostra sem reposição.
Caso não houvesse esta regra, poderíamos rodar o dado novamente com reposição, utilizando o argumento replace = TRUE na função.
Isto nos ajuda a entender o conceito de Independência de eventos, que no caso, aplica-se a rodar o dado com reposição, isto porque, rodar o dado na primeira vez não afeta o resultado da probabilidade na segunda. O que não podemos dizer sobre o caso de rodar o dado sem reposição, o que leva a termo eventos dependentes.
Distribuição de probabilidades
Uma distribuição de probabilidades é uma lista dos possíveis resultados que um evento pode ter, e como cada resultado é comum entre si. Elencaremos duas formas de distribuição de probabilidade: Discreta e Contínua
Discreta
Uma distribuição é considerada discreta quando seus números são contagens em formato de inteiros. Em relação ao dado, sua distribuição segue como discreta devido ao fato de que, teoricamente, seus resultados possuem a mesma probabilidade (1/6).
 Contínua
Contínua
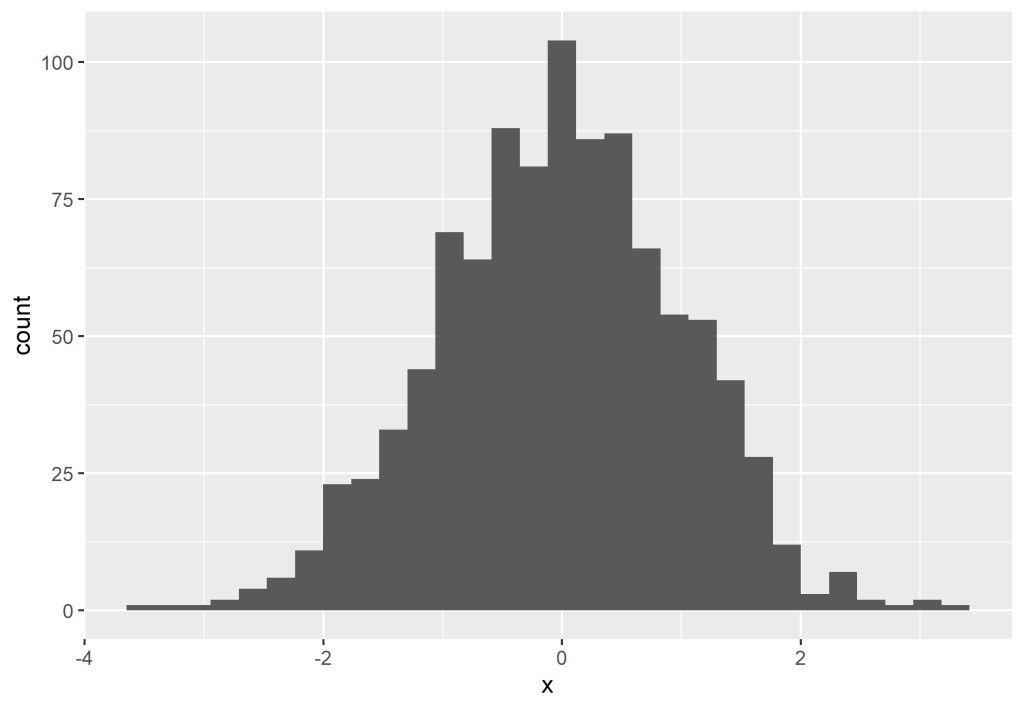
Uma distribuição é considerada contínua quando o resultado pode ser qualquer valor entre dois outros valores. Uma importante distribuição contínua pode ser representada pela distribuição normal, muito famosa pelo seu formato de sino. Esta distribuição, construída por um histograma, possui uma forma simétrica e o seu centro equivale a sua média.
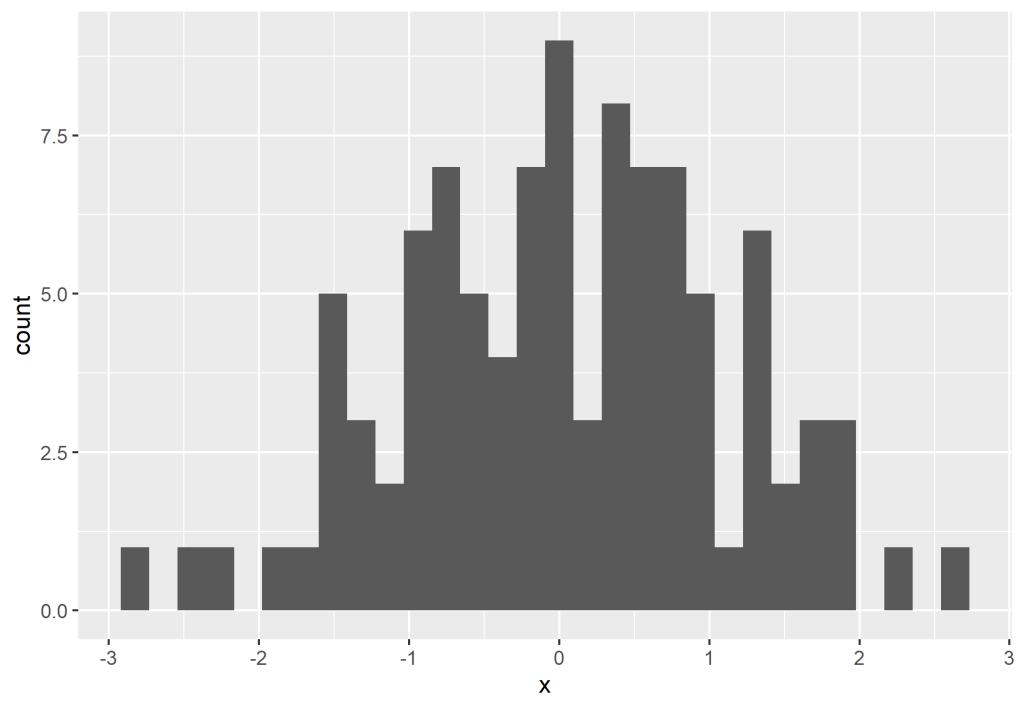
Podemos gerar uma distribuição normal utilizando a função rnorm.
Veja que o histograma acima não representa fielmente a distribuição normal perfeitamente, porém, se adicionarmos cada vez mais valores, poderemos ver que a distribuição cada vez mais se aproxima de uma normal.
Isso ocorre devido ao que é conhecido como Teorema Central do Limite, que permite dizer que quanto maior a amostra, mais a distribuição dos dados se tornam normais e próximas da média.
____________________________________________
Quer saber mais?
Veja nossos cursos de R e Python aplicados para a Análise de Dados e Economia