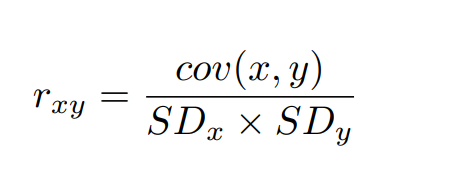A frase "correlação não implica causalidade" é bem difundida no campo da análise de efeito de uma variável X sobre Y. A frase é totalmente correta, mas mesmo que muitas vezes ditas, muitas pessoas ainda não entendem o porque é afirmado. Para entender melhor sobre essa questão, iremos realizar uma breve interpretação sobre o efeito de uma variável sobre a outra explicando o que é correlação e regressão utilizando o R, e por fim, discorreremos sobre o que é causalidade.
O que é correlação?
A correlação é uma medida que visa calcular a força da relação linear entre duas variáveis, principalmente de duas variáveis contínuas. A correlação de Pearson é a mais utilizada para representar este indicador, sendo definida como a covariância entre duas variáveis normalizada (i.e dividida) pelo produto de seus desvios padrão.
As duas questões mais importantes que devemos sempre lembrar sobre correlação são:
1) É uma relação linear, ou seja, uma linha linear de ajuste pode ser traçada em um gráfico de dispersão das duas variáveis para verificar visualmente esse ponto.
2) A força é bidirecional, ou seja, a força medida pela correlação exemplifica a relação entre as duas variáveis e não uma sobre a outra.
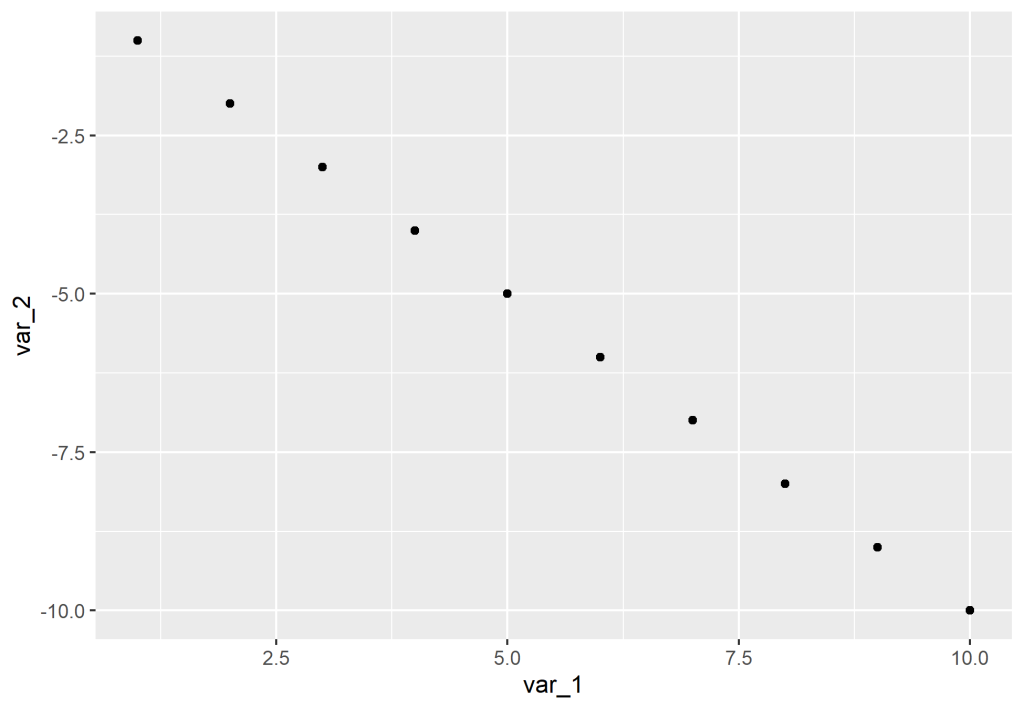
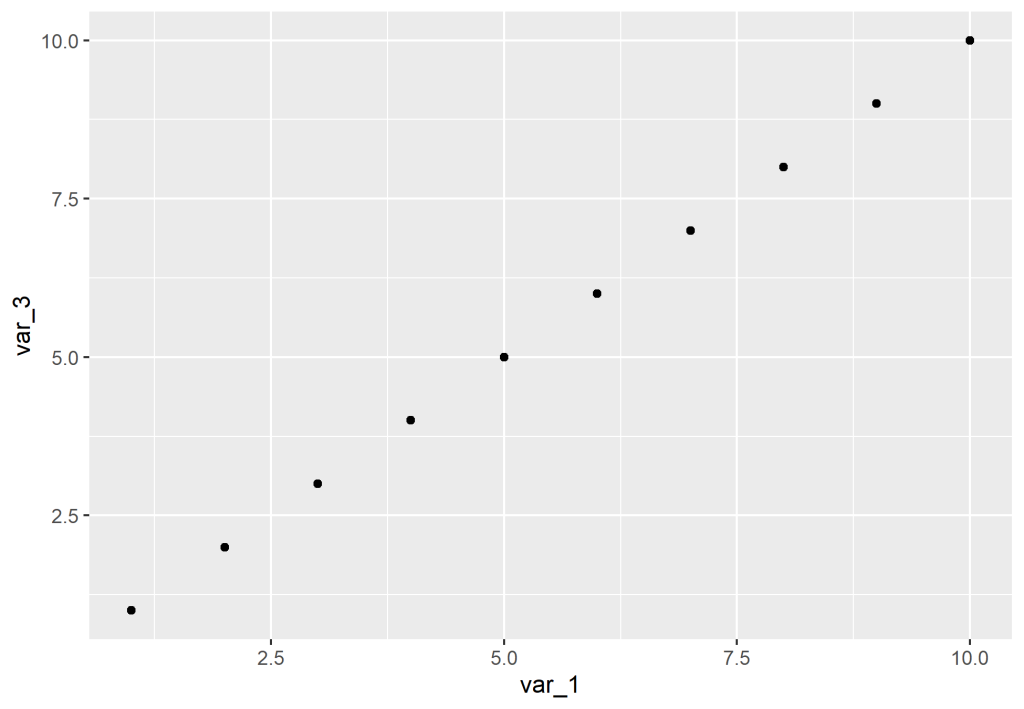
A correlação pode ser negativa, positiva ou nula (próxima de zero). Visualmente, podemos verificar estas três possíveis relações.
Como exemplo, utilizamos o dataset palmerpenguins para exemplificar a correlação entre as variáveis, construindo uma matriz de correlação. Vemos abaixo a estrutura do dataset, bem como as variáveis contínuas que podemos relacionar.
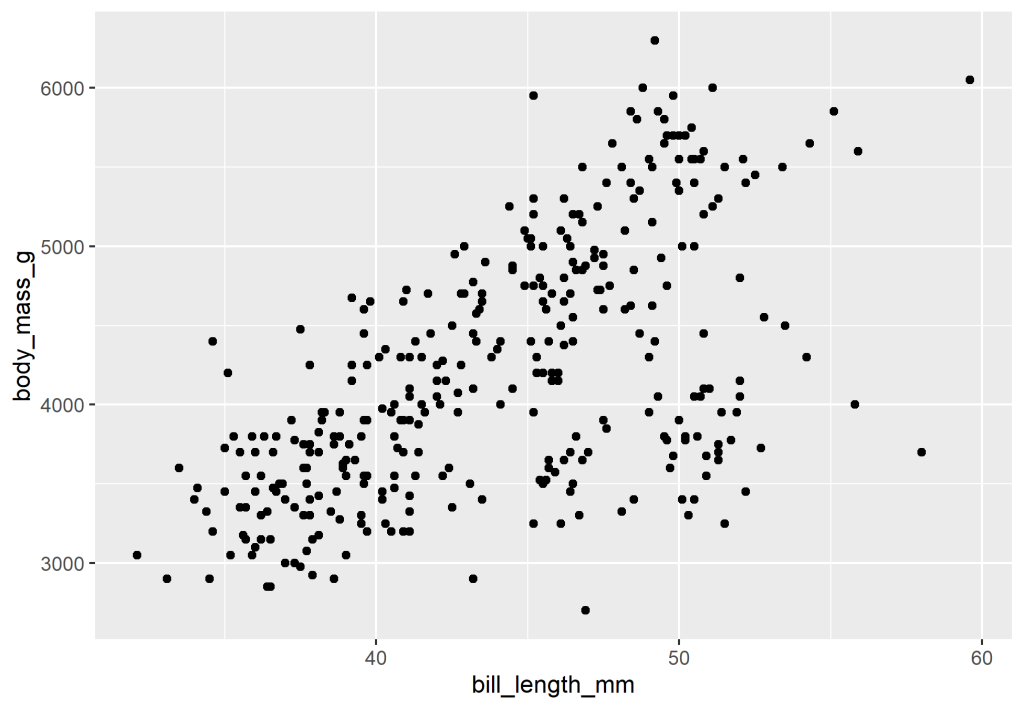
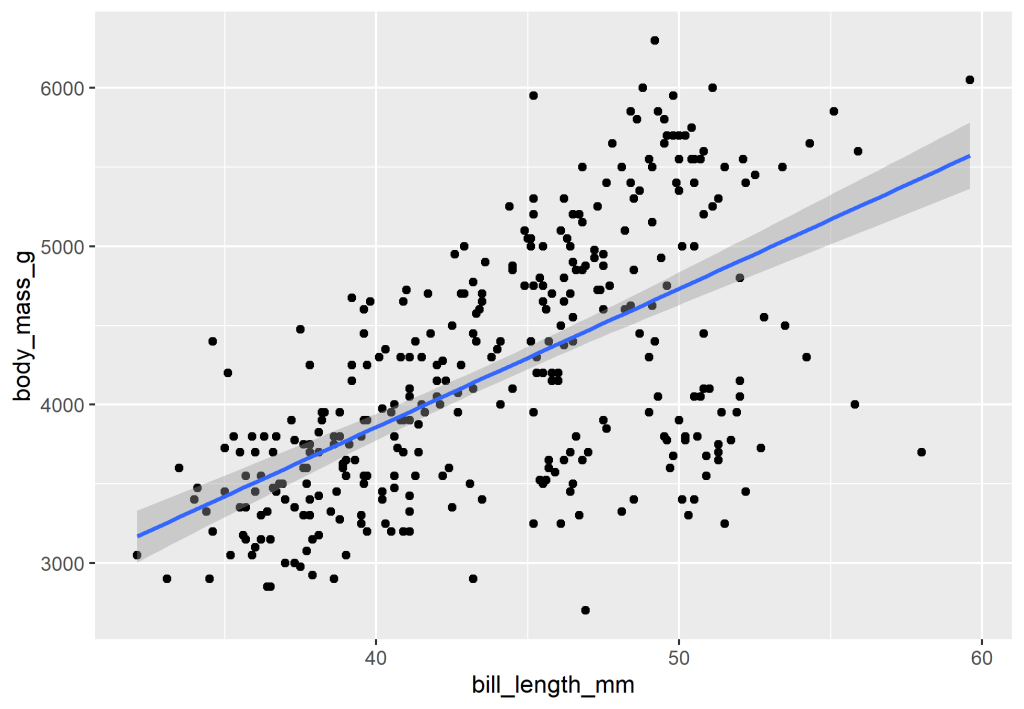
Além da matriz, também seria interessante ver a relação entre as variáveis através de um gráfico de dispersão de modo que possamos avaliar a relação linear entre as variáveis. No caso abaixo, visualizamos a relação de bill_length_mm (comprimento do culmen) e body_mass_g (massa corporal).
Existem diversos tipos de correlação, bem como métodos de inferências (dado que estamos lidando com amostras), sendo possível realizar testes de hipóteses. O pacote {correlation} facilita utilização destas ferramentas, porém, não iremos nos aprofundar sobre elas neste post.
Realizamos uma breve introdução ao conceito de correlação, vimos que podemos medir a força da relação entre duas variáveis, mas e se quisermos avaliar o efeito de uma variável X em Y? Para isso, podemos evoluir para a Regressão Linear.
Regressão Linear
Para podermos avaliar o possível efeito de uma variável em outra utilizamos a Regressão Linear. Como dito anteriormente, podemos traçar uma reta para verificar a linearidade das duas variáveis (isto porque a regressão linear também deve possuir uma relação linear, não é?), a questão aqui é que esta reta é expressa também através de uma equação e será através dela que iremos definir a relação entre a variável dependente e independente.
Em que Y será a variável dependente e X será a variável independente. é o intercepto,
é o coeficiente da regressão que vai ponderar o efeito de X sobre Y. Não trataremos sobre como calcular
, no qual ensinamos essa questão no nosso curso de Econometria.
O significa o termo de erro da nossa equação, isto é, caso calcularmos o efeito de X sobre Y, o termo de erro será a diferença entre o que estimamos e o valores reais, ou seja, toda a informação que não foi inserida na nossa equação. Para solucionar este ponto, podemos inserir dentro da equação as variáveis que carregam esta informação, evoluindo o nosso modelo para uma Regressão Linear Múltipla.
Como estamos trabalhando com uma amostra, também queremos inferir o efeito da regressão para a população. Podemos verificar este ponto através do teste t ou p valor dado um nível de confiança.
 Causalidade
Causalidade
E onde a causalidade entra em tudo isso? Afinal, correlação é uma forma ver a relação entre as duas variáveis, e a regressão é uma forma de ver o efeito de X em Y. Intuitivamente, já sabemos que a correlação não é o melhor método para buscar causalidade, sendo o segundo método mais apropriado.
Dizer que há causalidade em algo, significa dizer que há o uma variável causa efeito em outra. Entretanto, nem sempre é possível ter certeza desta questão, mesmo com indicadores estatísticos, portanto, é necessário mais que isso.
Um dos problemas que podemos tropeçar é a correlação espúria, que diz respeito quando há uma relação estatística entre duas variáveis, entretanto, essa relação é causada por pura coincidência ou por causa de uma terceira variável. Este é um dos diversos problemas que podemos ter ao realizarmos os cálculos entre duas variáveis.
Veja por exemplo a correlação entre bill_length_mm e flipper_length_mm (que diz respeito ao tamanho das asas do pinguim). Há uma força muito grande entre ambas, por que há esse efeito? E se fizéssemos um exemplo com regressão?
Vemos que há uma forte relação do efeito de uma sobre a outra. Mas podemos pensar, é possível mesmo que quanto maior a nadadeira do pinguim, maior será o comprimento de seu cúlmen? Não faz sentido lógico (por mais que eu não entenda de pinguins). É possível que uma terceira variável fora do modelo esteja influenciando ambas as variáveis (talvez a altura do pinguim?). De fato, devemos ter uma olhar crítico e mais dados em mãos para afirmar qualquer causalidade.
____________________________________________
Quer saber mais?
Veja nossos cursos de R e Python aplicados para a Análise de Dados e Economia
- R para Análise de Dados
- Python para Análise de Dados
- Gráficos com ggplot2
- Estatística usando R e Python
- Machine Learning usando o R
_____________________________________________
Referências
Mount, G. Advancing Into Analytics. Estados Unidos, O'Reilly Media, 2021.