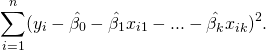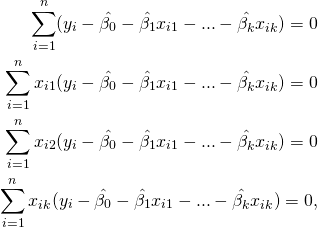Em post anterior das Dicas de R, vimos o modelo de regressão simples, onde pode ser explicado por uma única variável
. O problema básico desse tipo de análise é que ela faz uma suposição bastante forte, qual seja, que
não está correlacionado com o erro, dificultando a aplicação da condição ceteris paribus. A análise de regressão múltipla, por outro lado, é mais receptiva a esse tipo de condição, uma vez que ela permite que controlemos outros fatores que afetam
, adicionando os mesmos na equação. Assim, por suposto, se queremos explicar
, podemos utilizar
variáveis, como abaixo:
(1)
onde é o intercepto,
é o parâmetro associado a
. De modo a obter uma estimativa para 1, devemos observar que
(2)
Isto é, que todos os fatores no termo de erro não observado sejam não correlacionados com as variáveis explicativas. De modo a obter estimativas para os
parâmetros, é possível recorrer ao método de mínimos quadrados ordinários. Isto é, dado
(3)
onde é a estimativa de
, o método de MQO escolhe as estimativas
que minimizam a soma dos quadrados dos resíduos:
(4)
O problema acima pode ser resolvido por meio de cálculo multivariado, de onde obtemos as condições de primeira ordem
(5)
ou simplesmente, e
.
# Interpretação da equação de regressão de MQO
Suponha que tenhamos
(6)
O intercepto será então o valor previsto de
quando
. Já as estimativas
e
devem ser interpretadas como efeito parcial ou simplesmente ceteris paribus. Isto é,
(7)
de modo que obtemos a variação prevista em dadas as variações em
e
. Em particular, quando
é mantido fixo, de modo que
, teremos
(8)
Ou, simplesmente,
(9)
onde irá medir o efeito da variação de
em
, mantido
constante.
# Exemplo: equação do salário-hora
De modo a ilustrar, vamos considerar o exemplo 3.2 de Wooldridge (2003), em que o mesmo utiliza o conjunto de dados wage1, disponível no pacote wooldridge. Ele pode ser acessado como abaixo.
library(wooldridge) data(wage1) modelo = lm(log(wage) ~ educ+exper+tenure, data=wage1)
| Dependent variable: | |
| log(wage) | |
| educ | 0.092*** |
| (0.007) | |
| exper | 0.004** |
| (0.002) | |
| tenure | 0.022*** |
| (0.003) | |
| Constant | 0.284*** |
| (0.104) | |
| Observations | 526 |
| R2 | 0.316 |
| Adjusted R2 | 0.312 |
| Residual Std. Error | 0.441 (df = 522) |
| F Statistic | 80.391*** (df = 3; 522) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
De modo a obter a seguinte reta de regressão para o log do salário-hora
(10)
De onde se conclui, por exemplo, que o aumento de um ano na educação formal equivale a um aumento de 9.2% no salário-hora, mantidos exper e tenure fixos.
Quer aprender mais sobre econometria? Conheça nosso Curso de Introdução à Econometria usando o R.
_______________________
Wooldridge, J. M. 2013. Introductory Econometrics: A Modern Approach. Editora Cengage.