O que é Teste de Hipóteses

Teste de hipóteses é uma formulação estatística que visa confirmar ou negar determinada suposição de uma população, utilizando dados amostrais. A condução desse tipo de teste é de extrema importância para a área cientifica e de análise de dados, visto que é através destes métodos que pode-se estabelecer com maior confiança a afirmação de uma suposição. Neste post de hoje, introduziremos o teste de hipóteses e realizaremos um exemplo utilizando o R.

Ao analisarmos qualquer fato da vida real, sempre realizamos suposições, de forma a tentar estabelecer o que pode ser verdadeiro ou falso. De fato, através de interpretações e da lógica, podemos supor e inferir sensos comuns, entretanto, podemos realmente afirmar tudo desta forma?

As Hipóteses que criamos a partir desses sensos podem, de fato, serem testadas, através de métodos estatísticos. Utilizaremos um exemplo neste instante: ao pensarmos em todos os fatos históricos e sociais, (a depender, vivência) podemos supor que homens tendem a serem promovidos em uma proporção maior que mulheres. De fato, essa e qualquer suposição podem carregar altas cargas de subjetividade, então como podemos nos livrar ao máximo dessa subjetividade e afirmar com alta certeza uma suposição?

Para obter uma ideia sobre como podemos realizar esse procedimento, realizamos o Teste de Hipóteses, no qual podemos separar em sete passos.

Hipótese

A Hipótese, como dito, é uma suposição, e essa suposição é um parâmetro de população. Obviamente, não iremos conseguir realizar um teste na população, portanto, é necessário utilizar uma amostra para estimar esse ponto. Ou seja, através de um parâmetro populacional estabelecido, iremos estimar o seu ponto amostral. Existem diversos parâmetros populacionais. Abaixo elencamos três importantes.

Parâmetro Populacional	Notação	Ponto Estimado	Símbolos
Proporção da População	$\rho$	Proporção da Amostra	$\hat{\rho}$
Média populacional	$\mu$	Média amostral	Média populacional $\hat{\mu}$
Diferença na proporção da população	$\rho_1 - \rho_2$	Diferença na proporção da amostra	$\hat{\rho_1 }- \hat{\rho_2}$

No exemplo acima, o parâmetro da população de interesse é a diferença na proporção de populações $\hat{\rho_1 }- \hat{\rho_2}$
$$. Devemos utilizar desse meio para realizar um estudo.

Teste de Hipótese

O Teste de Hipótese consiste em teste entre duas hipóteses (suposições) que competem entre si:

A Hipótese Nula (H0), supõe que não há nenhum efeito ou diferença de um grupo para outro. Representa que "não há nada acontecendo".
A Hipóteses Alternativa (Ha) é a suposição que "compete" com a Hipótese Nula, e tenta se opor a ela.

Sendo assim, é possível criar as Hipóteses da seguinte maneira:

H0: homens e mulheres são promovidos na mesma taxa.
Ha: homens são promovidos a uma taxa maior que mulheres
Ha: mulheres são promovidas a uma taxa maior que homens
Ha: Há uma diferença na taxa de promoção de mulheres em relação aos homens.

A escolha das hipóteses acima será crucial para a montagem e verificação do estudo, bem como cada hipótese será analisada de uma forma diferente, a depender da forma que foi criada. Se a busca é por uma diferença na proporção de homens que são promovidos a uma taxa maior que mulheres, significa que a hipótese é unicaudal (o mesmo para o contrário), se a alternativa diz que há apenas uma diferença nas taxas de promoção, não importando se maior ou menor, dizemos que é uma hipótese bicaudal. Essa diferenciação será útil para quando quisermos descobrir se o parâmetro estimado é significativo.

Para simplificar, escolheremos apenas uma hipótese alternativa: homens são promovidos a uma taxa maior que mulheres (unicaudal a direita). Portanto, o teste fica dessa forma:

H0: $\hat{\rho_h}- \hat{\rho_m}$ = 0
Ha: $\hat{\rho_h}- \hat{\rho_m}$ > 0

Teste Estatístico

O Teste Estatístico é um ponto a ser estimado, isto é, dentre as N quantidades de observações da amostra, iremos criar a estimativa de um único ponto calculado, que neste caso é a diferença na proporção da amostra entre duas categorias $\hat{\rho_h}- \hat{\rho_m}$

Teste Estatístico Observado

Teste Estatístico Observado é o valor encontrado através do teste estatístico postulado no passo anterior, ou seja, é a estimativa na vida real da estatística amostral calculada. Portanto, devemos encontrar esse valor da diferença de proporções com $\hat{\rho_h}- \hat{\rho_m}$

Distribuição Nula

A Distribuição Nula é a distribuição da amostra do teste estatístico assumindo que a hipótese nula H0 é verdadeira. Vamos dizer que não há discriminação de gênero em promoções de emprego no problema pesquisado (que significa dizer sob H0), então, sob H0, como o teste estatístico varia devido a uma variação amostral? Veja bem, o ponto estimado é calculado com base nos dados da amostra, se os valores da amostra variarem, a estimativa do ponto também irá mudar, correto? Portanto, como a diferença na proporção amostral $\hat{\rho_h}- \hat{\rho_m}$ , irá variar devido a amostragem sob H0? Esse é um passo delicado, visto que existe diversas formas de realizar o procedimento.

O procedimento acima chama-se distribuição amostral, e devemos ter em mente que a distribuição nula é a distribuição amostral assumindo que a hipótese nula H0 é verdadeira.

p-valor

O p-valor é a probabilidade de obter o teste estatístico sob H0 (lembrando que supomos que H0 é verdadeiro) de forma que o valor do teste seja extremo. Basicamente: o quão surpresos ficaríamos com o resultado encontrado no teste estatístico observado? Seria difícil dizer o quanto um valor na diferença nas proporções para diferentes amostras seria significativo e deveria ser considerado ou não. No caso do exemplo, na hipótese de que não há discriminação de promoções, caso o teste estatístico observado tenha um valor extremo, deveríamos considerar de que há de fato uma discriminação de promoções, o que nos levaria a rejeitar H0. Ou seja, o p-valor nos ajudará a quantificar a probabilidade de ocorrência desse valor extremo.

Nível de Significância

É recomendado definir em testes de hipóteses o nível de significância do estudo, denotado por α. Esse valor define a área que devemos aplicar o p-valor, isto é, se o p-valor ficar abaixo de α, devemos rejeitar a hipótese nula H0. Ao contrário, se o p-valor ficar acima de α, não podemos rejeitar H0.

Conduzindo o teste de hipóteses

Os passos citados acima fazem parte de um framework construído por Allen Downey, nomeado de "There is only one test", que facilitou o processo do teste de hipóteses para qualquer variável e teste estatístico. Para conduzir o teste de hipóteses, utilizaremos o pacote {infer}, que possui funções criadas voltadas para este fim e foram totalmente baseadas nos passos de Alllen Downey.

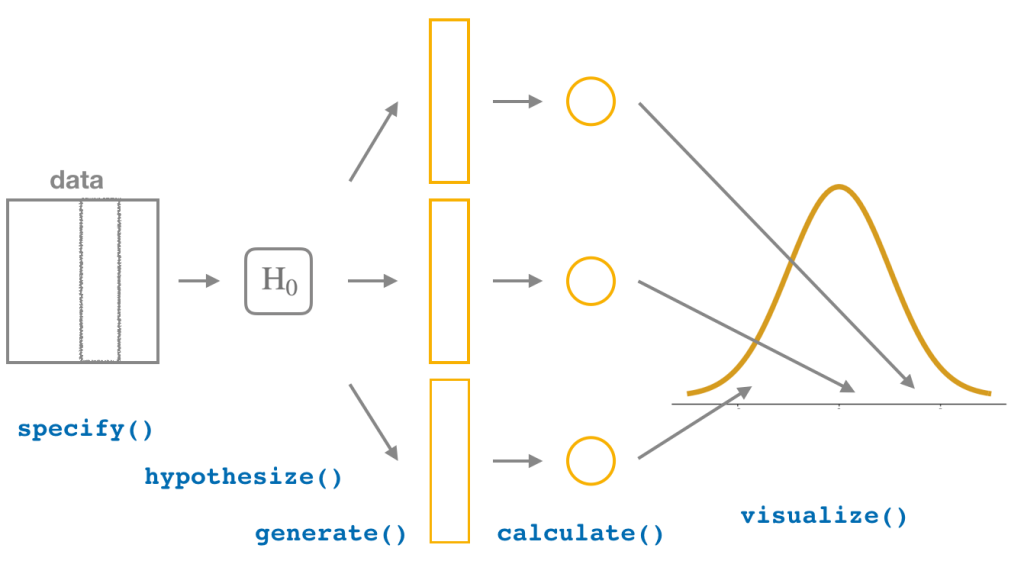
Workflow - Teste de Hipóteses com o pacote {infer}

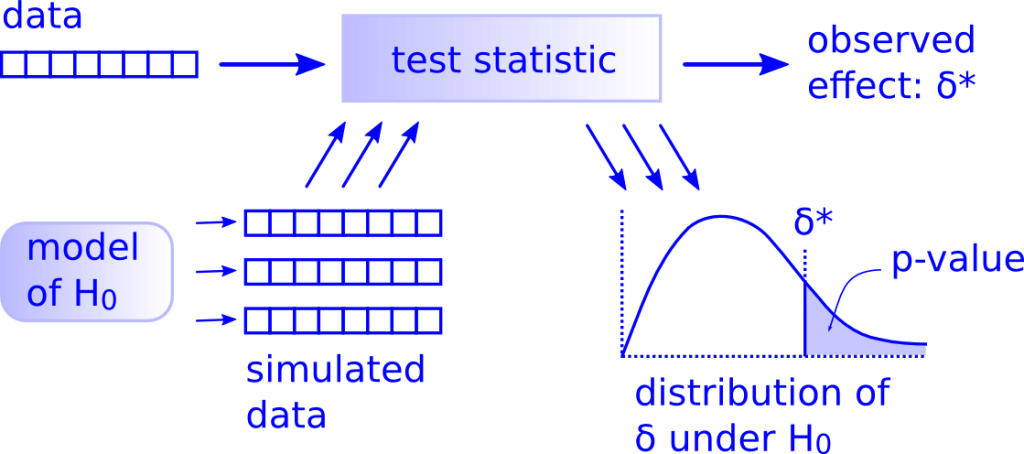
Workflow - "There is only one test" Allen Downey

A primeira imagem, retirada do site do pacote {infer}, demonstra o workflow de suas função e dos procedimentos do teste de hipótese. Na segunda imagem, o workflow construído por Allen Downey através do artigo "There is Only one test". Veja as similaridade entre as imagens. As funções do pacote representam os passos propostos por Allen Downey. Cada função é proposta da seguinte forma:

specify() - Específica as variáveis de interesse ou que devem se relacionar do data frame;

hyphotesize() - Define a Hipótese nula H0. Ou seja, cria um modelo para o universo, assumindo H0 como verdadeiro;

generate() - "Mistura" a amostra, assumindo H0 como verdadeiro;

calculate() - Calcula o teste estatístico de interesse, tanto o observado, quanto o simulado;

visualize() - Visualiza o resultado da distribuição nula e computa o p-valor para comparar a distribuição nula com o teste estatístico observado.

Exemplo com {infer}

Realizamos toda a explicação do Teste de Hipóteses utilizando como exemplo a discriminação na promoção de mulheres em empresas. Para continuar com o mesmo exemplo no R, utilizaremos o dataset promotions, que contém dados de uma pesquisa realizada na década de 1970, no qual foi distribuído currículo idênticos de empregados em empresas da indústria bancária, apenas diferenciando-se pelo nome da pessoa (permitindo supor o sexo da pessoa).

O dataset possui 48 observações, contendo a coluna com o nome "decision", identificando se houve promoção ou não, e outra coluna chamada "gender" identificando se o currículo entregado era de uma mulher ou de um homem. A coluna "id" apenas identificado as observações.

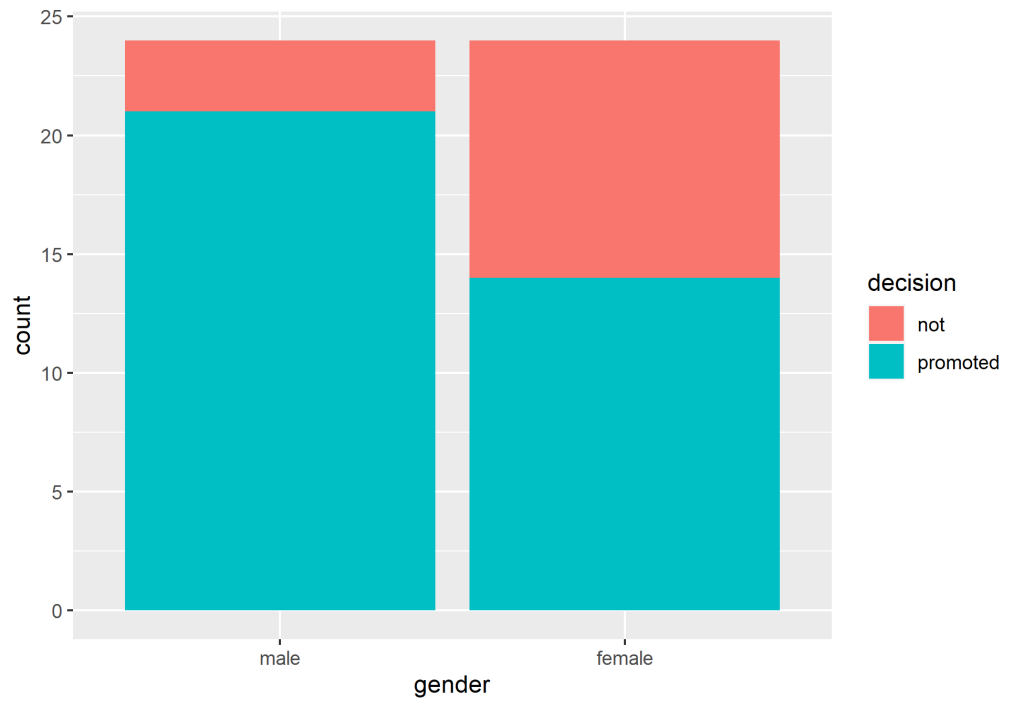
O primeiro passo, além de carregar os pacotes, é examinar o dataset, conduzindo uma breve análise exploratória.

<br />

É possível perceber que de fato houve uma diferença no tratamento entre homens e mulheres neste caso. A questão é: podemos dizer que é significativo? É possível realizar uma inferência deste problema? Seguimos com as funções do pacote {infer} para realizar o teste de hipóteses.

Primeiro definimos a construção da distribuição nula. Veja que seguimos todos os passos descritos acima. Definimos a formula da especificação (já intuitivamente pensando no parâmetro a ser estimado), a hipótese nula, a criação da amostragem, sendo gerado 1000 repetições através da permutação. Calculamos a distribuição referenciando o parâmetro (diff in props - diferença em proporções) e a ordem que queremos calcular.

Em seguida, construímos o teste estatístico observado, utilizando apenas duas funções: specify e calculate.

<br />

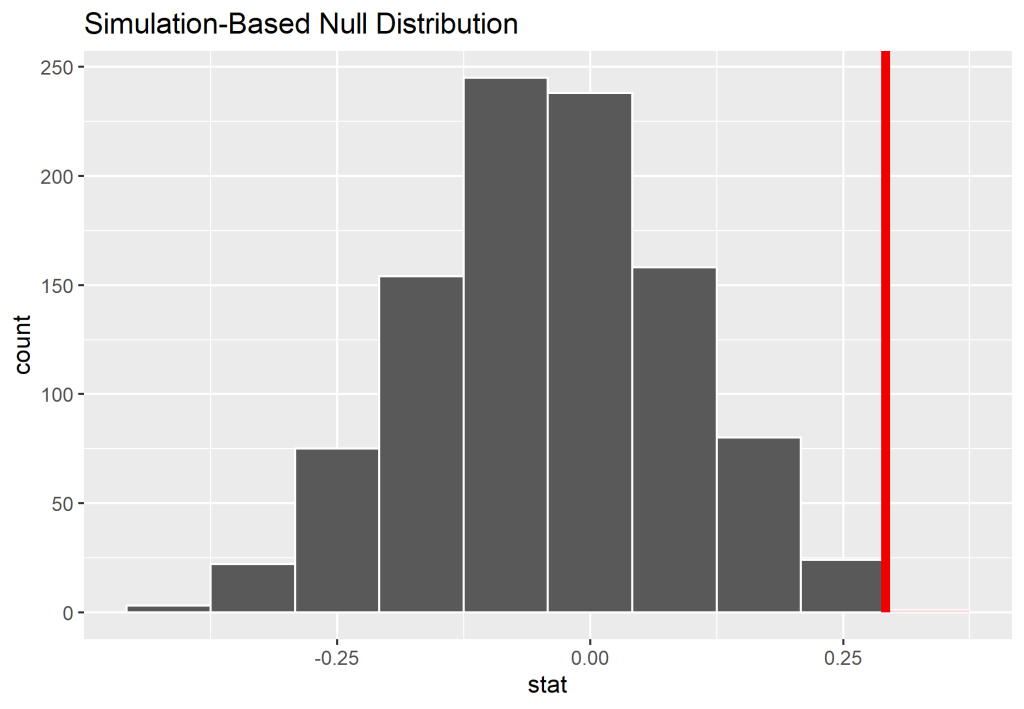
Por fim, podemos obter o p-valor com a função get_p_value, bem como podemos visualizar onde se encontra dentro da distribuição nula. Vemos que de fato, o p-valor é menor que 5% e que obtemos um teste estatístico observado extrema, nos levando a rejeitar a hipótese de que homens e mulheres são promovidos na mesma taxa.

<br />

Quer saber mais?

Veja nossos cursos de R e Python aplicados para a Análise de Dados e Economia

_____________________________________________

Referências

Downey, Allen. There is Only one test

Kim, Y. Albert. Ismay, Chester. Statistical Inference via Data Science A ModernDive into R and the Tidyverse

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Criando um Dashboard de análise de Ações no Python

Analisando séries temporais no Python e esquecendo de vez o Excel

Cálculo do Retorno Econômico de uma Política Pública

Simplificando análises de dados manuais do Excel usando o Python

Outros artigos relacionados

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Colocar modelos em produção pode ser um grande desafio. Lidar com custos monetários, infraestrutura operacional e complexidades de códigos e ferramentas pode acabar matando potenciais projetos. Uma solução que elimina todos estes obstáculos é a recém lançada Shinylive. Neste artigo mostramos um exemplo com um modelo de previsão para o preço do petróleo Brent.

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Manter relatórios diários com dados e análises atualizados é um desafio, pois envolve várias etapas: coleta de dados, tratamento de informações, produção de análises e atualização de relatório. Para superar este desafio algumas ferramentas como Python + Quarto + GitHub podem ser usadas para automatizar tudo que for automatizável. Neste artigo mostramos um exemplo com dados do mercado financeiro.

Criando um Dashboard de análise de Ações no Python

Um Dashboard é um painel de controle que consolida uma variedade de informações sobre um determinado objeto de estudo em um ou mais painéis. Ele simplifica significativamente o processo de análise de dados, oferecendo uma visão global e fácil de entender. Uma maneira simples de construir um Dashboard para acompanhar uma ação específica é utilizando duas ferramentas: Quarto e Python. Neste post, mostramos o resultado da criação de um Dashboard de Ação.