Composição do preço
De acordo com a Petrobras, o preço da gasolina nacional é composto por, em R$/litro:
![\[\underbrace{Y}_\text{Preço na bomba} = \underbrace{R}_\text{Refinaria} + \underbrace{A}_\text{Etanol Anidro} + \underbrace{F}_\text{Imp. Federais} + \underbrace{E}_\text{Imp. Estaduais} + \underbrace{M}_\text{Margem}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-50237b163d00c7de610fb2fcde17685b_l3.png "Rendered by QuickLaTeX.com")
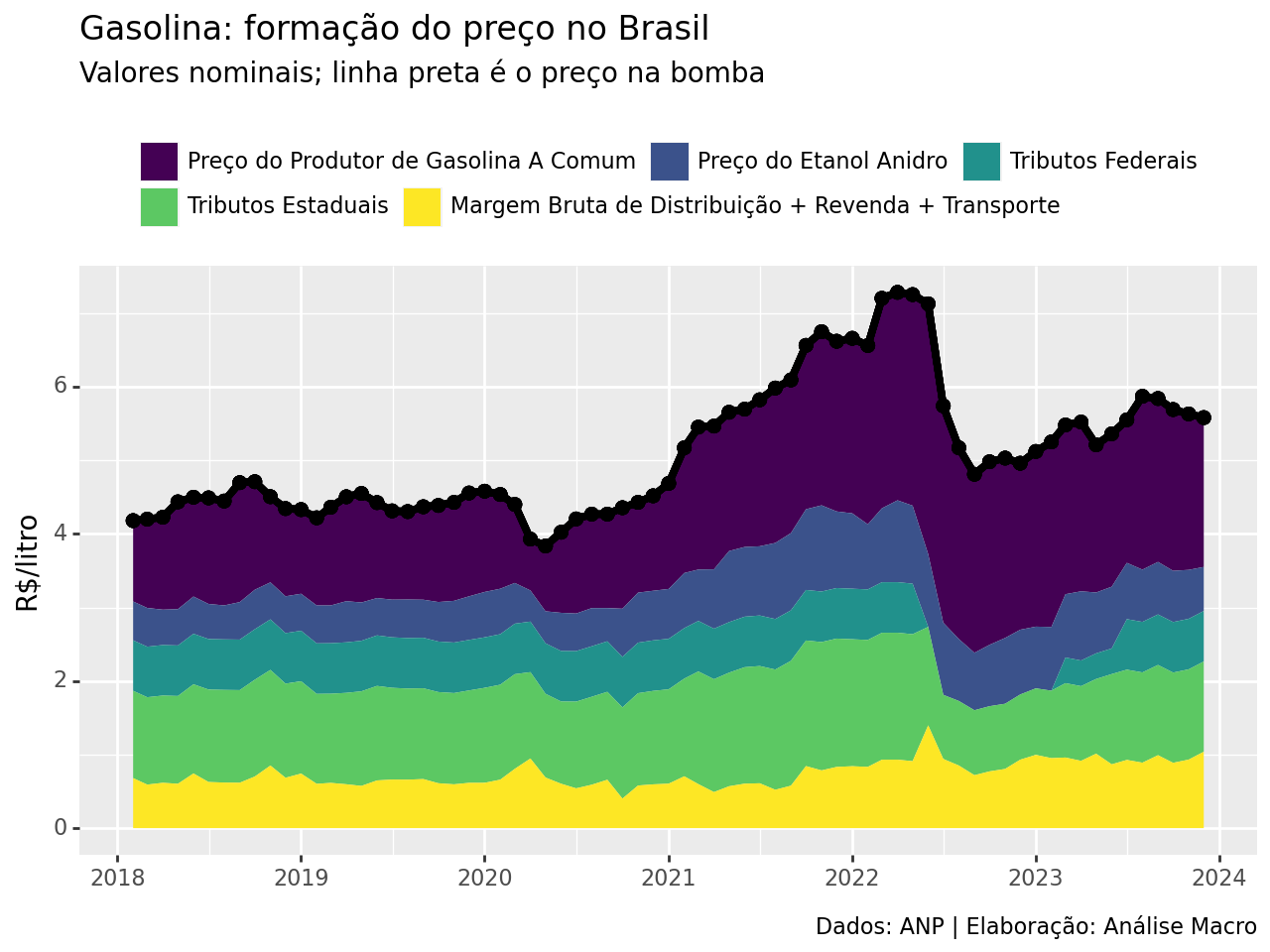
O que significa que o preço da gasolina na bomba é uma soma entre o preço da gasolina na refinaria, o custo da mistura obrigatória de etanol anidro, o valor de impostos federais ad rem (CIDE, PIS/PASEP e COFINS), estaduais (ICMS) e o valor da margem de distribuição e revenda para os postos. O gráfico abaixo apresenta a evolução temporal destes componentes.
Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.
Política de paridade de preços
No que se refere ao preço na refinaria, até ano passado, o principal player neste mercado, a Petrobras, seguia a política de paridade de preços de importação. Isso significa que variações no preço internacional do petróleo podiam ser absorvidas, de forma que o preço doméstico acompanharia estas variações. Isso trouxe, em cerca medida, uma boa previsibilidade sobre o preço da gasolina.
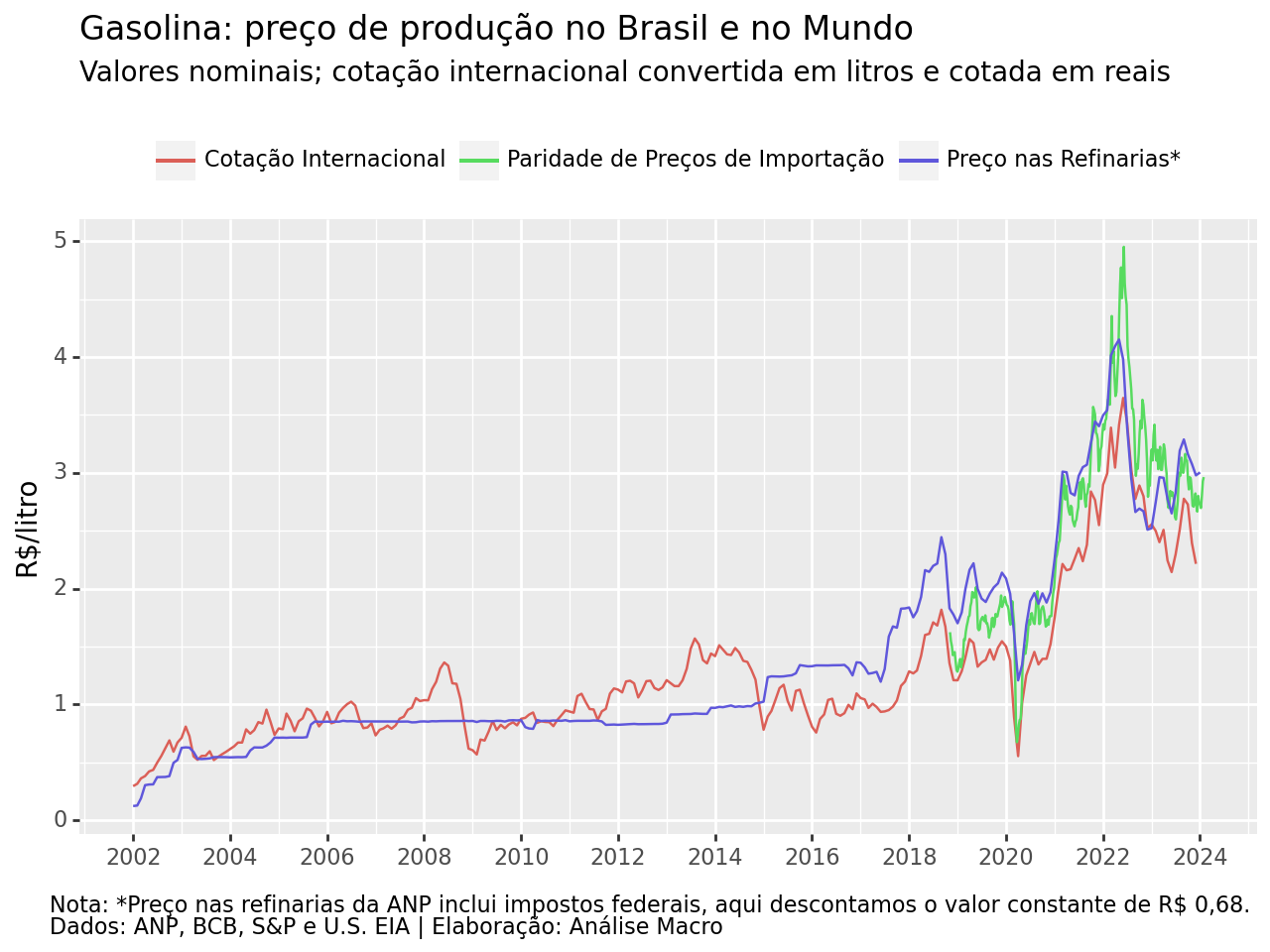
Com o fim desta política, no entanto, a definição do preço da gasolina na refinaria, que varia por volta de 1/3 do preço na bomba, virou uma caixa preta (apesar do discurso de transparência do governo/Petrobras). O gráfico abaixo compara o preço da gasolina internacional cotado em reais e convertido em litros com o preço na refinaria (R$/litro), além do preço PPI:
Modelo
Inicialmente, vamos construir um modelo de previsão simples através de uma regressão linear, especificado pela fórmula acima. Ao checar a estacionariedade das séries temos que a maioria é I(1), portanto transformamos todas as séries com a variação absoluta. Com isso, temos os seguintes resultados de coeficientes estimados pelo modelo:
OLS Regression Results
==============================================================================
Dep. Variable: Y_delta R-squared: 0.858
Model: OLS Adj. R-squared: 0.848
Method: Least Squares F-statistic: 80.06
Date: Fri, 09 Feb 2024 Prob (F-statistic): 1.15e-26
Time: 08:08:18 Log-Likelihood: 67.603
No. Observations: 72 AIC: -123.2
Df Residuals: 66 BIC: -109.5
Df Model: 5
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0062 0.012 0.527 0.600 -0.017 0.029
R_delta 0.5220 0.062 8.486 0.000 0.399 0.645
A_delta 1.2679 0.198 6.400 0.000 0.872 1.663
F_delta 0.0555 0.149 0.372 0.711 -0.242 0.353
E_delta 1.6822 0.165 10.194 0.000 1.353 2.012
M_delta 0.8551 0.107 8.004 0.000 0.642 1.068
==============================================================================
Omnibus: 2.049 Durbin-Watson: 2.129
Prob(Omnibus): 0.359 Jarque-Bera (JB): 1.337
Skew: 0.214 Prob(JB): 0.512
Kurtosis: 3.512 Cond. No. 18.4
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Os resíduos do modelo parecem adequados, assim como os coeficientes estimados, com exceção da variação de Tributos Federais ( 
). Está série é problemática por conta de valores constantes e próximos ou iguais a zero. Há alternativas e soluções que poderiam ser abordadas, mas aqui seguiremos ignorando esta questão.
Cenários
Com vistas a utilizar este modelo para fins de previsão, assumimos o que se segue para as variáveis exógenas:
= 0 (último valor observado constante para o futuro);
= 0 (último valor observado constante para o futuro);- = 0 (último valor observado constante para o futuro);
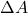= 0 (último valor observado constante para o futuro).
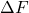= 0 (último valor observado constante para o futuro);
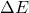= 0 (último valor observado constante para o futuro);
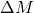= 0 (último valor observado constante para o futuro).Para 
, usando o preço internacional cotado em reais e convertido em litros, usamos os seguintes cenários:
- WTI aumenta até US$ 100 e câmbio em R$ 6;
- WIT último valor observado permance constante no futuro e câmbio em R$ 5;
- WTI diminui até US$ 50 e câmbio em R$ 4.
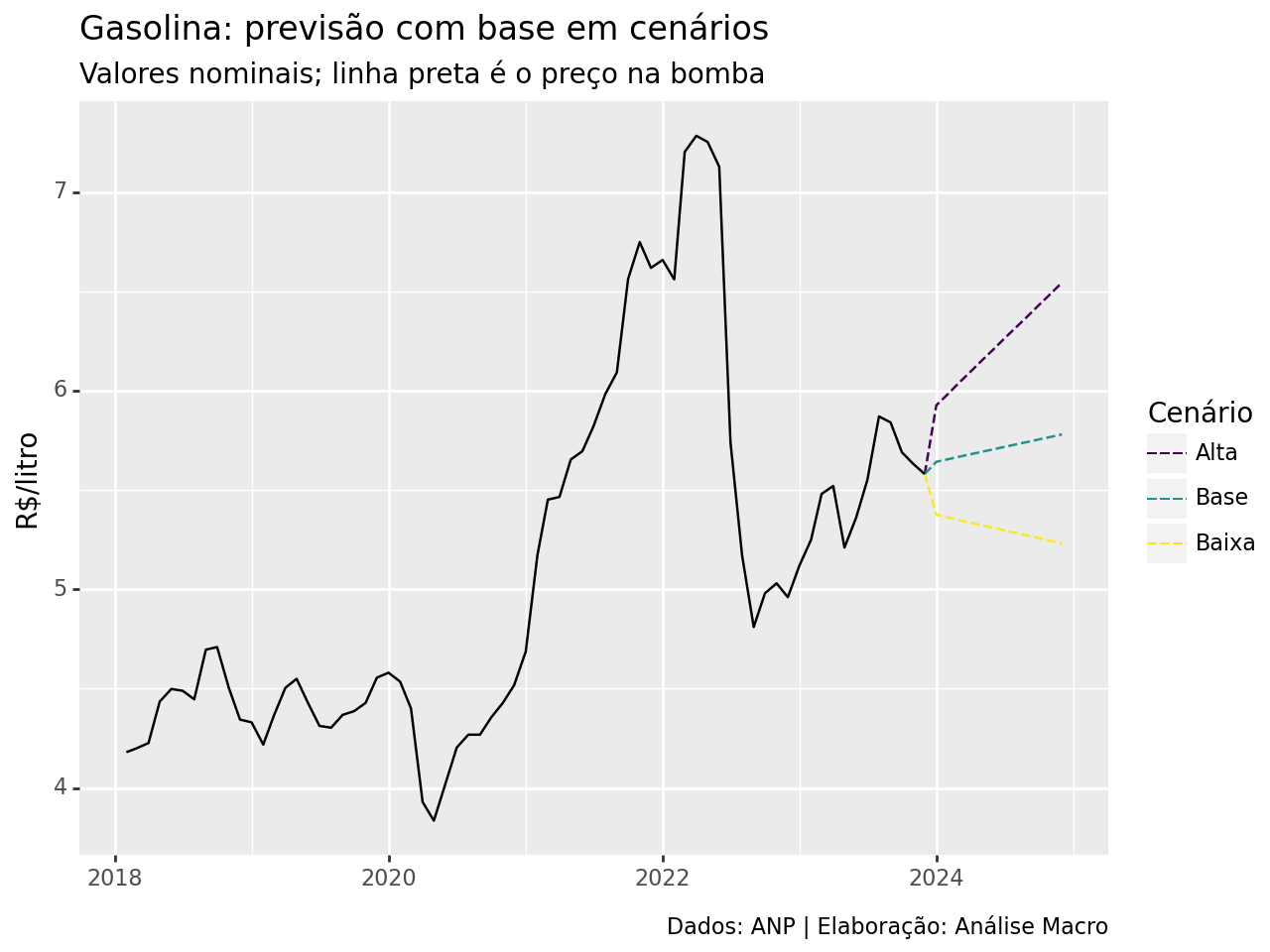
Com base nestes cenários, temos a seguinte previsão 12 períodos a frente para o preço da gasolina na bomba (R$/litro):
Conclusão
Neste exercício exploramos os dados públicos sobre o preço da gasolina no Brasil, sua composição, evolução temporal, políticas associadas e, por fim, construímos um modelo simples de previsão. Com um modelo em mãos, o analista pode cenarizar o comportamento futuro da série da forma como preferir. Todos os procedimentos foram feitos usando a linguagem de programação Python.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.
Referências
BCB (2019). Mensuração de riscos para a inflação associados a preços de energia. Estudo Especial nº 61/2019.
BCB (2022). Repasse do preço do petróleo em reais para a inflação e mensuração de riscos. Relatório de Inflação 03/2022.
Felipe Camargo (2022). Projetando o preço da gasolina brasileira. https://flcamargo90.medium.com/projetando-o-pre%C3%A7o-da-gasolina-brasileira-e611fa8829ef
