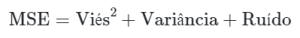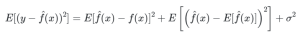Ao criar um modelo de previsão para séries temporais há dois possíveis problemas comuns que podem acontecer, em termos simples:
- Sobreajuste (overfitting): o modelo estimado explica “perfeitamente” a variável de interesse; uma simples comparação gráfica dos dados observados com os dados de ajuste entregues pelo modelo permite verificar que a distância entre o observado e o estimado tende a ser mínima. Ao tentar utilizar este modelo para previsão de dados futuros, não observados, a tendência é que o modelo erre bastante.
- Sub-ajuste (underfitting): o modelo estimado explica “insatisfatoriamente” a variável de interesse; uma simples comparação gráfica dos dados observados com os dados de ajuste entregues pelo modelo permite verificar que a distância entre o observado e o estimado tende a ser grande. Ao tentar utilizar este modelo para previsão de dados futuros, não observados, a tendência é que o modelo erre de forma semelhante.
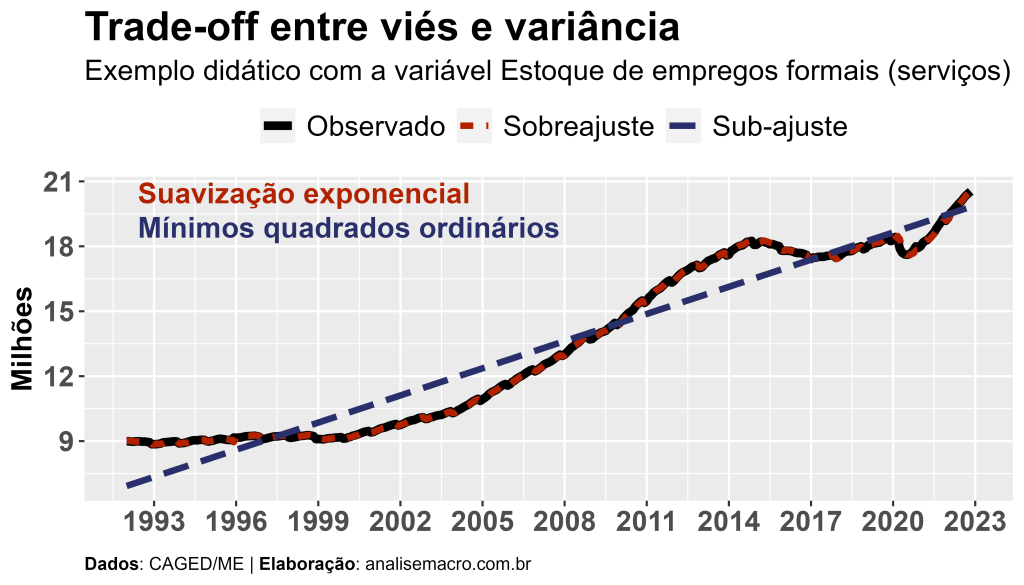
No gráfico acima são apresentados, como exemplo, dados observados da variável Estoque de empregos formais no setor de serviços (CAGED/ME), assim como dois modelos didáticos que buscam explicar essa variável. O modelo mais simples, mínimos quadrados ordinários, traça uma reta de tendência para as observações da amostra, o que leva a grandes distâncias em relação aos dados observados. Já o modelo mais complexo, suavização exponencial, se sobrepõe aos dados observados, capturando praticamente toda a dinâmica da série temporal.
Até aqui estamos falando de modelos de previsão, mas olhando apenas para o ajuste dos mesmos com a amostra utilizada para estimar seus devidos parâmetros. Em geral, para problemas de previsão há maior interesse em analisar o erro de “fora da amostra”, ou seja, para dados que o modelo ainda não conhece. Sendo assim, é comum separar a série temporal em duas amostras: uma de treino, usada para estimar os parâmetros do modelos, e outra de teste, usada para realizar previsões e comparar com os dados observados, chegando ao erro de previsão:
ou seja, os valores observados (que ficaram omitidos na estimação) menos o que foi previsto “fora da amostra” pelo modelo. Com essa medida é possível analisar e comparar a acurácia dos modelos. Isso é feito, geralmente, com métricas baseadas no erro de previsão, como ME, MSE, RMSE, etc.
Separando a série temporal deste exemplo, Estoque de empregos formais (serviços), de forma a termos as 12 últimas observações para a amostra de teste e o restante para treino, reestimamos os modelos acima e geramos previsões, comumente chamadas de “pseudo” fora da amostra. Ao calcular o erro de previsão e as métricas citadas, temos que:
| Amostra | Modelo | ME | MSE | RMSE |
|---|---|---|---|---|
| Treino | Suavização exponencial | 0.0057841 | 0.0017843 | 0.0422410 |
| Treino | Mínimos quadrados ordinários | 0.0000000 | 1.0849871 | 1.0416271 |
| Teste | Suavização exponencial | 0.1896337 | 0.0487402 | 0.2207719 |
| Teste | Mínimos quadrados ordinários | 0.3153532 | 0.1950269 | 0.4416185 |
O que aconteceu? Os números da tabela retratam os dois problemas levantados no início do texto: o modelo mais complexo apresenta sobreajuste na amostra de treino (dados que ele conhece) e erra muito na amostra de teste (dados desconhecidos); já o modelo mais simples apresenta sub-ajuste na amostra de treino e erra de forma “semelhante” na amostra de teste. Ou seja, o modelo de suavização exponencial apresenta um erro 5x maior na amostra de teste em relação a amostra de treino, analisando pelo RMSE, enquanto que o modelo de mínimos quadrados ordinários apresenta um erro menor na amostra de teste em relação a amostra de treino (o RMSE cai, aproximadamente, pela metade).
Entretanto, também é interessante notar que apesar dessas disparidades, o modelo com sobreajuste tem um erro menor fora da amostra em relação ao modelo com sub-ajuste, o que pode torná-lo um candidato final para previsão efetivamente fora da amostra. Ou seja, não existem regras, é necessário analisar os modelos com vistas aos objetivos do exercício estatístico. Nem sempre um modelo bem ajustado será o melhor para previsão e nem sempre um modelo mal ajustado será um modelo pior para previsão. Geralmente, busca-se um modelo que minimize o erro de previsão e um modelo “meio termo” pode ser o mais razoável para essa finalidade no longo prazo.
Mas o que isso tem a ver com viés e variância?
Tudo, pois o erro de previsão na amostra de teste pode ser proveniente tanto de sobreajuste quanto de sub-ajuste. Para averiguar isso podemos decompor a métrica de erro, o MSE, em três componentes:
O viés é o quadrado da diferença entre as previsões e os valores observados, e pode ser entendido como o “erro sistemático” do modelo de previsão, após ter sido ajustado para diversos conjuntos de dados independentes, ou seja, para diferentes “realizações” do modelo. Modelos com sub-ajuste (baixa complexidade) tendem a apresentar um viés alto. Em termos simples, imagine desenhar, com alguma aleatoriedade, várias linhas de regressão linear sobre a série temporal acima: em média, a distância entre as linhas e as observações será alta.
A variância é a média do quadrado da diferença entre as previsões e o valor “esperado” das previsões, e pode ser entendido como o quanto as previsões variam, em média, para uma determinada observação, após o modelo também ter sido ajustado para diversos conjuntos de dados independentes, ou seja, para diferentes “realizações” do modelo. Modelos com sobreajuste (alta complexidade) tendem a apresentar uma variância alta. Em termos simples, imagine desenhar, com alguma aleatoriedade, várias curvas de regressão polinomial sobre a série temporal acima: conforme há mais parâmetros determinando o formato da curva, a variedade de previsões geradas aumentará.
O ruído é um termo aleatório de erro, ou seja, uma parcela da métrica de erro que não é explicada nem pelo viés e nem pela variância.
Matematicamente1, isso é o mesmo que:
Sendo assim, o objetivo do profissional que trabalha com previsão é explorar uma especificação de modelo, f(x), de modo a obter previsões menos erráticas, tendo em vista que ela pode aumentar tanto o viés quanto a variância do erro. Em modelos sub-ajustados, de baixa complexidade, a maior parcela do erro de previsão advém do viés; já em modelos sobreajustados, de alta complexidade, a maior parcela do erro de previsão advém da variância. Escolher uma especificação de modelo entre estes dois extremos é o que se chama de dilema, ou trade-off, entre viés e variância.
Saiba mais
Códigos de reprodução em R deste exercício estão disponíveis para membros do Clube AM da Análise Macro.
Para se aprofundar no assunto confira os cursos aplicados de R e Python da Análise Macro:
- Trilha de Machine Learning e Econometria: https://conteudosam.com.br/pacotes/econometria-e-machine-learning/
- Econometria: https://analisemacro.com.br/cursos/econometria/introducao-a-econometria/
- Análise de Séries Temporais: https://conteudosam.com.br/cursos/analise-de-series-temporais/
Referências
Ely, R. A. (2016, August 25). O tradeoff entre viés e variância em três gráficos. Regis A. Ely Blog. http://regisely.com/blog/bias-variance/
Wilber, J. & Werness, B. (2021, January). The bias variance tradeoff. MLU-EXPLAIN. https://mlu-explain.github.io/bias-variance/
Notas de rodapé
- Veja mais em Bias variance decomposition de Rob J Hyndman: https://robjhyndman.com/files/2-biasvardecomp.pdf↩︎