Para mitigar estes riscos, modelos de probabilidade de recessão podem trazer informações relevantes para a tomada de decisão. Neste artigo mostramos uma aplicação destes modelos para a economia norte-americana, usando o ferramental de pacotes do Python.
Aprenda a coletar, processar e analisar dados no Workshop Do Zero à Análise de Dados Econômicos e Financeiros usando Python, se inscreva aqui!
Modelos
Existem diversos modelos que podem auxiliar na estimativa de uma próxima crise financeira. De modo geral, estes modelos podem ser categorizados dentro da área de Inteligência Artificial, que engloba os modelos de machine learning e deep learning. Como exemplo, utilizaremos aqui 3 modelos que poderiam ser categorizados1 dentro de machine learning:
- Regressão logística (saiba mais aqui)
- Florestas Aleatórias (saiba mais aqui)
- K Vizinhos Mais Próximos (saiba mais aqui)
A ideia por trás destes modelos é obter uma estimativa numérica da probabilidade de acontecer uma recessão em um determinado período no tempo. Quando esta probabilidade (valor entre 0 e 100) é alta, há indicativos de que uma crise possa acontecer.
Este exercício é derivado de um outro anterior, onde estes modelos são aplicados para demonstrar uma aplicação de machine learning em análise macroeconômica.
Dados
Para estimar a probabilidade de recessão para a economia dos Estados Unidos (EUA), selecionamos os seguintes dados (disponíveis publicamente):
- Indicador de recessão mensal produzido pelo NBER (FRED/USREC)
- Taxa de juros do tesouro americano de curto (3 meses) prazo (FRED/TB3MS)
- Taxa de juros do tesouro americano de longo (10 anos) prazo (FRED/GS10)
- Total de empregados na economia, excluindo agrícolas (FRED/PAYEMS)
- Índice de inflação urbana (FRED/CPIAUCSL)
Além disso, é incluída uma variável de diferença entre a taxa de longo e a de curto prazo, para determinar o ângulo da curva de juros. Para o juro longo são incluídas defasagens de 3, 6, 9 e 12 meses.
Nossa variável de interesse é o indicador de recessão mensal produzido pelo NBER adiantado 12 meses. Ou seja, nosso interesse é prever se vai haver uma recessão nos 12 meses subsequentes.
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
A tabela abaixo mostra as últimas observações da tabela de dados coletada online pela API do FRED:
| USREC | GS10 | TB3MS | PAYEMS | CPIAUCSL | |
|---|---|---|---|---|---|
| DATE | |||||
| 2023-10-01 | 0 | 4.80 | 5.34 | 156832 | 307.531 |
| 2023-11-01 | 0 | 4.50 | 5.27 | 157014 | 308.024 |
| 2023-12-01 | 0 | 4.02 | 5.24 | 157304 | 308.742 |
| 2024-01-01 | 0 | 4.06 | 5.22 | 157533 | 309.685 |
| 2024-02-01 | 0 | 4.21 | 5.24 | 157808 | 311.054 |
A tabela abaixo apresenta as novas variáveis construídas conforme indicado acima:
| date | USREC | GS10 | TB3MS | PAYEMS | CPIAUCSL | slope_yield | GS10_lag3 | GS10_lag6 | GS10_lag9 | GS10_lag12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 525 | 2023-10-01 | NaN | 4.80 | 5.34 | 156832 | 307.531 | -0.54 | 3.90 | 3.46 | 3.53 | 3.98 |
| 526 | 2023-11-01 | NaN | 4.50 | 5.27 | 157014 | 308.024 | -0.77 | 4.17 | 3.57 | 3.75 | 3.89 |
| 527 | 2023-12-01 | NaN | 4.02 | 5.24 | 157304 | 308.742 | -1.22 | 4.38 | 3.75 | 3.66 | 3.62 |
| 528 | 2024-01-01 | NaN | 4.06 | 5.22 | 157533 | 309.685 | -1.16 | 4.80 | 3.90 | 3.46 | 3.53 |
| 529 | 2024-02-01 | NaN | 4.21 | 5.24 | 157808 | 311.054 | -1.03 | 4.50 | 4.17 | 3.57 | 3.75 |
Treinamento
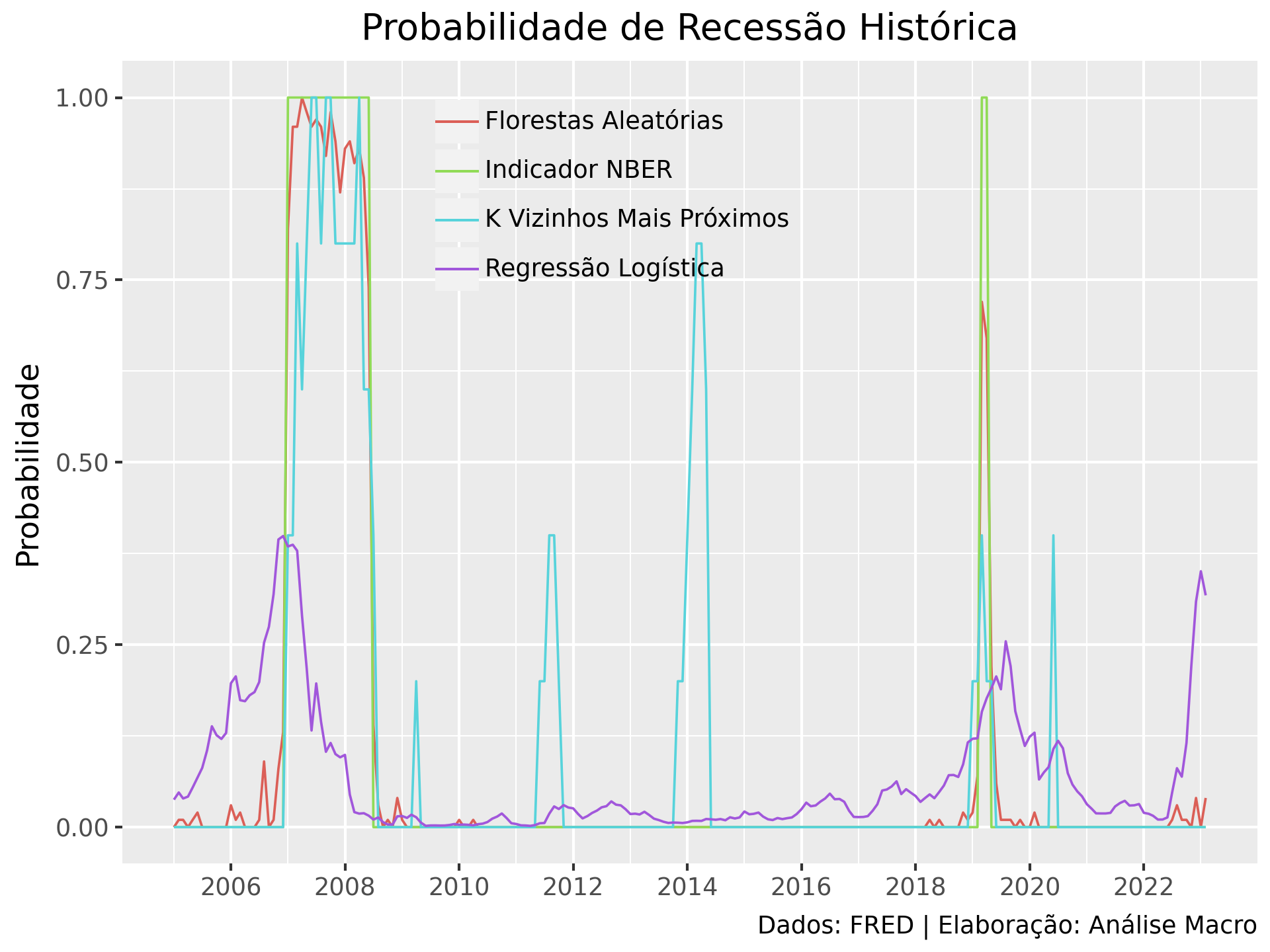
Para treinar os modelos, utilizaremos a amostra completa de dados, sem separar em treino/teste ou validação cruzada, visando simplificar os procedimentos. O gráfico abaixo apresenta o ajuste dos modelos aos dados históricos:
Cenários
De modo a utilizar estes modelos para prever o futuro, ou seja, a probabilidade de recessão a partir do último período de dados disponíveis, devemos fornecer ao modelo os dados futuros das variáveis explicativas. Isso é comumente referido como “cenários” para as variáveis exógenas.
Nestes modelos há 4 variáveis exógenas:
- Taxa curta
- Taxa longa
- Total de empregados
- Inflação
As demais variáveis de entrada no modelo são derivadas destas.
Vamos gerar 3 cenários para cada variável, de modo a ter 3 estimativas da probabilidade de recessão nos EUA:
- Cenário pessimista: taxa curta aumenta linearmente até 15%, taxa longa aumenta linearmente até 10%, total de empregados diminui linearmente até 140000 e inflação aumenta linearmente até 350 no final de 2024.
- Cenário base: tudo permanece constante até o final de 2024.
- Cenário otimista: taxa curta diminui linearmente até 2.7%, taxa longa diminui linearmente até 4%, total de empregados aumenta linearmente até 160000 e inflação diminui linearmente até 275 no final de 2024.
Observação: considerar unidade de medida das variáveis (disponível na fonte).
As tabelas abaixo apresentam alguns valores para os cenários das variáveis:
| GS10 | TB3MS | PAYEMS | CPIAUCSL | slope_yield | GS10_lag3 | GS10_lag6 | GS10_lag9 | GS10_lag12 | |
|---|---|---|---|---|---|---|---|---|---|
| date | |||||||||
| 2024-10-01 | 8.0700 | 11.746667 | 145936.0 | 337.0180 | -3.676667 | 6.6225 | 5.1750 | 4.0600 | 4.80 |
| 2024-11-01 | 8.5525 | 12.560000 | 144452.0 | 340.2635 | -4.007500 | 7.1050 | 5.6575 | 4.2100 | 4.50 |
| 2024-12-01 | 9.0350 | 13.373333 | 142968.0 | 343.5090 | -4.338333 | 7.5875 | 6.1400 | 4.6925 | 4.02 |
| 2025-01-01 | 9.5175 | 14.186667 | 141484.0 | 346.7545 | -4.669167 | 8.0700 | 6.6225 | 5.1750 | 4.06 |
| 2025-02-01 | 10.0000 | 15.000000 | 140000.0 | 350.0000 | -5.000000 | 8.5525 | 7.1050 | 5.6575 | 4.21 |
| GS10 | TB3MS | PAYEMS | CPIAUCSL | slope_yield | GS10_lag3 | GS10_lag6 | GS10_lag9 | GS10_lag12 | |
|---|---|---|---|---|---|---|---|---|---|
| date | |||||||||
| 2024-10-01 | 4.0700 | 3.546667 | 159269.333333 | 287.0180 | 0.523333 | 4.1225 | 4.1750 | 4.0600 | 4.80 |
| 2024-11-01 | 4.0525 | 3.335000 | 159452.000000 | 284.0135 | 0.717500 | 4.1050 | 4.1575 | 4.2100 | 4.50 |
| 2024-12-01 | 4.0350 | 3.123333 | 159634.666667 | 281.0090 | 0.911667 | 4.0875 | 4.1400 | 4.1925 | 4.02 |
| 2025-01-01 | 4.0175 | 2.911667 | 159817.333333 | 278.0045 | 1.105833 | 4.0700 | 4.1225 | 4.1750 | 4.06 |
| 2025-02-01 | 4.0000 | 2.700000 | 160000.000000 | 275.0000 | 1.300000 | 4.0525 | 4.1050 | 4.1575 | 4.21 |
| GS10 | TB3MS | PAYEMS | CPIAUCSL | slope_yield | GS10_lag3 | GS10_lag6 | GS10_lag9 | GS10_lag12 | |
|---|---|---|---|---|---|---|---|---|---|
| date | |||||||||
| 2024-10-01 | 4.21 | 5.24 | 157808 | 311.054 | -1.03 | 4.21 | 4.21 | 4.06 | 4.80 |
| 2024-11-01 | 4.21 | 5.24 | 157808 | 311.054 | -1.03 | 4.21 | 4.21 | 4.21 | 4.50 |
| 2024-12-01 | 4.21 | 5.24 | 157808 | 311.054 | -1.03 | 4.21 | 4.21 | 4.21 | 4.02 |
| 2025-01-01 | 4.21 | 5.24 | 157808 | 311.054 | -1.03 | 4.21 | 4.21 | 4.21 | 4.06 |
| 2025-02-01 | 4.21 | 5.24 | 157808 | 311.054 | -1.03 | 4.21 | 4.21 | 4.21 | 4.21 |
Previsão
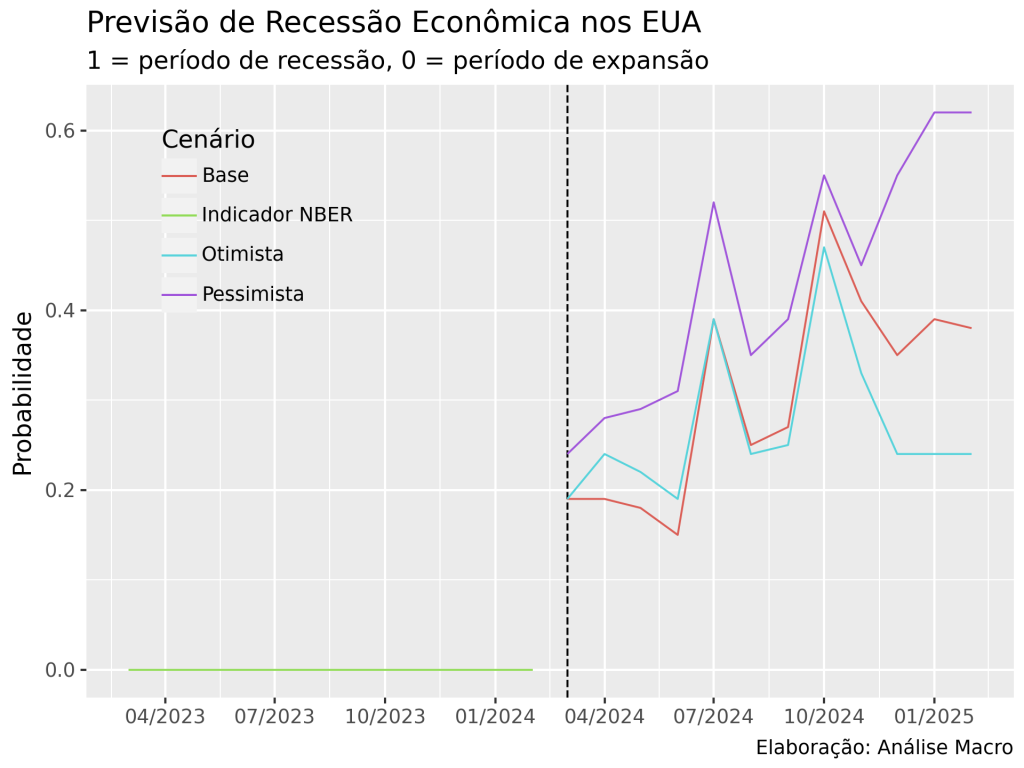
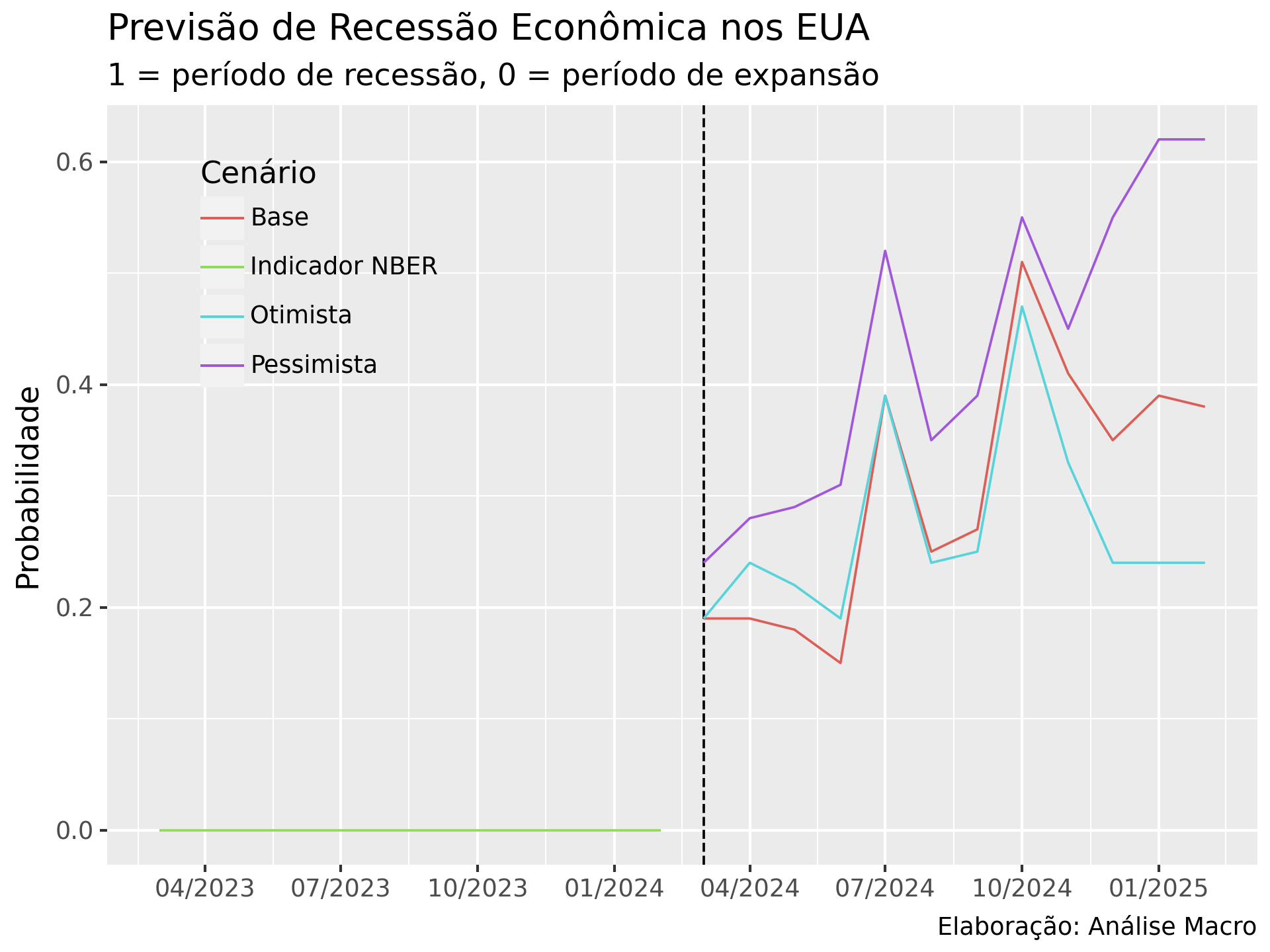
Para gerar previsão para o futuro escolhemos arbitrariamente o modelo Florestas Aleatórias. O gráfico abaixo exibe as previsões de probabilidade de recessão para a economia dos EUA conforme cada cenário:
Conclusão
Fazer investimentos sem analisar dados é como atirar no escuro. Ninguém quer estar numa posição errada na hora que uma nova crise estourar. Para mitigar estes riscos, modelos de probabilidade de recessão podem trazer informações relevantes para a tomada de decisão. Neste artigo mostramos uma aplicação destes modelos para a economia norte-americana, usando o ferramental de pacotes do Python.
Notas de rodapé
- Estas categorizações são discutíveis.↩︎
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.