Como garantir que uma previsão pontual não ultrapasse um determinado limite? Por exemplo, se a variável de interesse para a previsão é "número de pessoas empregadas", sabemos que ou o valor da série é "zero pessoas empregadas" ou algum valor positivo. Pelo processo gerador dos dados, não faz sentido, neste caso, um modelo gerar previsões negativas. Sendo assim, neste artigo mostramos o caminho para estabelecer restrições em previsões pontuais e as ferramentas da linguagem R para tal.
É comum querer que as previsões sejam positivas ou exigir que elas estejam dentro de algum intervalo especificado, [a, b]. Ambas estas situações são relativamente fáceis de lidar usando transformações.
Restrição positiva
Para impor uma restrição de valores positivos, podemos simplesmente trabalhar na escala logarítmica. Se denotarmos as observações originais como y1, ..., yT e as observações transformadas como w1, ..., wT, então wt = log(yt).
Os logaritmos são úteis porque são interpretáveis: as alterações em um valor em log são alterações relativas (ou percentuais) na escala original. Portanto, se o log de base 10 for usado, um aumento de 1 na escala logarítmica corresponde a uma multiplicação de 10 na escala original. Se algum valor da série original for zero ou negativo, a transformação logarítmica não é possível.
Por exemplo, se a série de interesse para previsão é "número de pessoas empregadas", então a série pode assumir valores iguais a zero ou positivos. Nesse caso, tudo que você precisa fazer é:
- Transformar a série original yt para escala logarítmica: wt = log(yt + 1)
- Estimar o modelo para wt e gerar as previsões gt
- Transformar as previsões gt de volta para a escala original: zt = exp(gt) - 1
A transformação log(yt + 1) é comumente usada para superar a limitação das transformações logarítmicas preservando a não negatividade, em dados que contêm zeros. Neste caso são duas transformações, log() e +1.
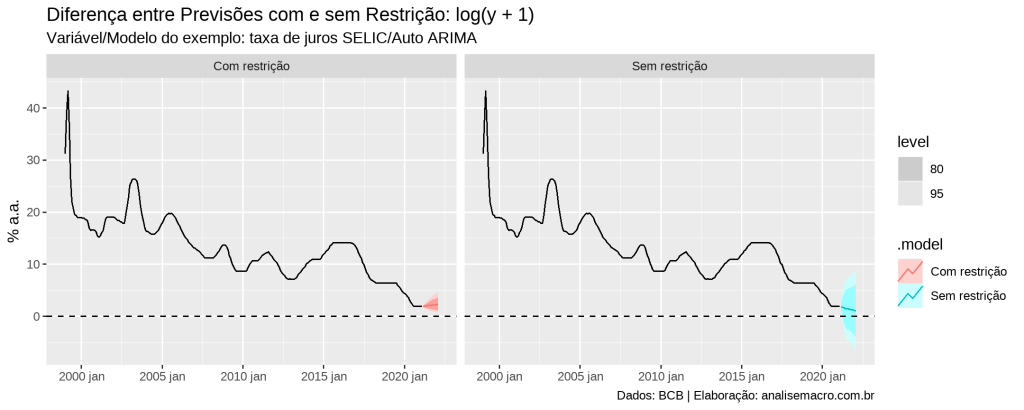
Em um exemplo com dados reais, usando como variável de interesse a taxa de juros SELIC (% a.a., BCB), sobre a qual é razoável pensar que assuma valores positivos em tempos normais da economia brasileira, o resultado da previsão com e sem restrição positiva seria algo parecido com isso:
Neste exemplo fica claro a importância da utilização da restrição: quando a restrição não é imposta o modelo gera previsões negativas (considerando o intervalo de confiança) para a variável de interesse, o que pode ser errôneo a depender da variável.
O procedimento de colocar isso em prática é relativamente simples usando a linguagem R. Você pode, por exemplo, utilizar o pacote {fable} que lida automaticamente com transformações simples como essa do exemplo, além de permitir outros tipos de transformações customizadas.
Saiba mais
Para ter acesso aos códigos desse exercício, torne-se Membro do Clube AM.
Para se aprofundar no assunto confira os cursos aplicados de R e Python da Análise Macro:
- Trilha de Machine Learning e Econometria: https://conteudosam.com.br/pacotes/econometria-e-machine-learning/
- Econometria: https://analisemacro.com.br/cursos/econometria/introducao-a-econometria/
- Análise de Séries Temporais: https://conteudosam.com.br/cursos/analise-de-series-temporais/