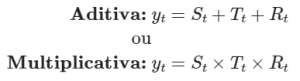Análise de séries temporais é um conjunto de técnicas para extrair informações e características úteis para o entendimento desse tipo de dado. A compreensão do comportamento da série temporal pode servir para diversos contextos e finalidades, como para a previsão nas áreas de economia, finanças e meteorologia, ou para detecção de sinais nas áreas de controle de engenharia, processamento de sinal, dentre outras.
Analisar séries temporais pode ser uma tarefa complexa e vasta, podendo as abordagens utilizadas para a análise de dados temporais serem divididas em domínio da frequência ou tempo, métodos paramétricos ou não paramétricos e métodos lineares e não lineares. Dentro de cada uma dessas divisões de abordagens ainda podem haver diversas outras subdivisões.
Portanto, nesse artigo vamos apresentar algumas técnicas de análise de séries temporais, focando em métodos de visualização das principais características dos dados temporais. O objetivo não é “abraçar o mundo” apresentando todas as abordagens e técnicas disponíveis, mas sim apresentar o essencial para “sair do zero” e que é útil para grande parte dos casos e aplicações.
A seguir, vamos explorar algumas técnicas e métodos de análise de séries temporais, focando em abordagens de visualização gráfica das características dos dados temporais.
Gráfico de linha
Para começar a entender uma série temporal e suas características, a primeira visualização de dados útil é o gráfico de linha. Com ele é possível ter uma “pista” visual sobre a série temporal, quando o objetivo é responder perguntas como:
- A série temporal apresenta alguma tendência (crescente ou decrescente)?
- A série temporal apresenta valores atípicos (outliers)?
- A série temporal apresenta variações periódicas (sazonalidade)?
- A série temporal apresenta comportamento (não)linear?
Apesar de o gráfico de linha não ser tão sofisticado para responder algumas dessas perguntas, ele serve para um primeiro palpite rápido e efetivo.
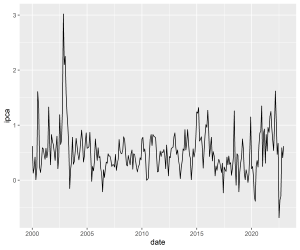
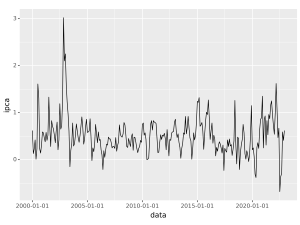
Abaixo exemplificamos como gerar um gráfico de linha para a série temporal Índice Nacional de Preços ao Consumidor Amplo (IPCA). Os dados são mensais, de janeiro de 2000 a dezembro de 2022, a unidade de medida é variação % e a fonte é o IBGE.
R
Código
# A tibble: 6 × 2
date ipca
<date> <dbl>
1 2000-01-01 0.62
2 2000-02-01 0.13
3 2000-03-01 0.22
4 2000-04-01 0.42
5 2000-05-01 0.01
6 2000-06-01 0.23Código
Python
Código
ipca
Date
2000-01-01 0.62
2000-02-01 0.13
2000-03-01 0.22
2000-04-01 0.42
2000-05-01 0.01Código
Analisando o gráfico, rapidamente podemos concluir que:
- A inflação brasileira possui uma variação constante em torno de ~0,5%;
- Valores atípicos já aconteceram nesses mais de 20 anos de dados e provavelmente podem acontecer de novo;
- Parece haver quedas da variação % mensal no período de inverno.
Estas são conclusões que mesmo um não economista poderia pontuar, apenas olhando os dados. Note que, porém, a análise pode mudar se os dados mudarem (janela amostral de dados diferente, período de hiperinflação, etc.).
Gráfico de sazonalidade
Para investigar com maior profundidade variações fixas e periódicas em uma série temporal, a chamada sazonalidade, os gráficos de sazonalidade podem ajudar. Estes gráficos, em geral, apresentam os valores da série temporal no eixo Y e a frequência no eixo X. Se a série é mensal, por exemplo, então no eixo X são dispostos os meses.
O propósito de analisar uma série temporal por um gráfico de sazonalidade é responder algumas destas perguntas:
- Existe um padrão sazonal na série temporal?
- Em qual período a variação sazonal acontece?
- A sazonalidade varia em magnitude ao longo do tempo?
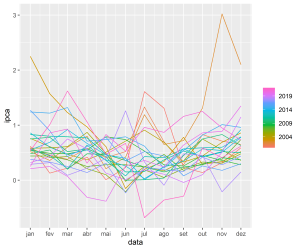
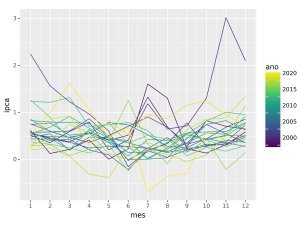
Abaixo exemplificamos como gerar um gráfico de sazonalidade para a série temporal Índice Nacional de Preços ao Consumidor Amplo (IPCA). Os dados são mensais, de janeiro de 2000 a dezembro de 2022, a unidade de medida é variação % e a fonte é o IBGE.
R
Código
Python
Código
Analisando o gráfico de sazonalidade fica claro um padrão de inflação menor na metade do ano e maior no final/início, apesar de discrepâncias acontecerem em determinados anos. Sendo assim, um modelo de previsão para essa série temporal, por exemplo, precisa produzir previsões coerentes com esse comportamento esperado dos dados.
Gráfico de decomposição: sazonalidade, tendência, ruído
Podemos dizer que uma série temporal é resultado de algumas pequenas “peças” que, quando juntas, formam a série que observamos, por exemplo, em um gráfico de linha. Em outras palavras, podemos decompor uma série temporal em alguns componentes para, então, analisá-los individualmente, fazer ajustes, transformações ou remoções.
Para tal, começamos assumindo que a série temporal possa ser decomposta de maneira:
onde:
yt é a série temporal observada;
St é o componente de sazonalidade;
Tt é o componente de tendência;
Rt é o componente de ruído (flutuações aleatórias).
Dessa forma, podemos analisar somente a tendência da série ou podemos remover a sazonalidade da série para obter a série “sazonalmente ajustada”, dentre outras análises possíveis.
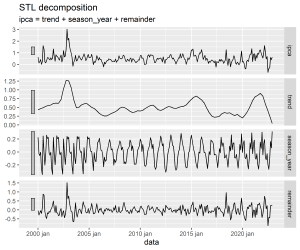
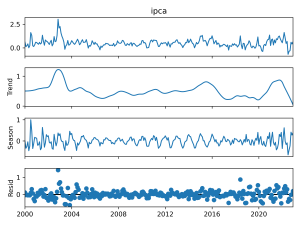
Abaixo exemplificamos como gerar um gráfico de decomposição para a série temporal Índice Nacional de Preços ao Consumidor Amplo (IPCA). Os dados são mensais, de janeiro de 2000 a dezembro de 2022, a unidade de medida é variação % e a fonte é o IBGE.
R
Código
Python
Código
Analisando o gráfico de decomposição podemos observar que:
- A tendência da série variou bastante no período (crises, recessões, ciclos?);
- A sazonalidade da série é forte, porém também variou bastante no período;
- O que sobra, o ruído, é relativamente comportado em períodos em que a economia esteve “comportada”.
Existem vários métodos de estimação/decomposição para obter os componentes da série temporal, a maioria deles são complicados ou demandam muito para um exercício introdutório, não havendo um consenso sobre o uso. Algumas instituições estatísticas, como o IBGE, usam os métodos X-11/SEATS e variações deles (X-12-ARIMA, X-13-ARIMA-SEATS, etc.), enquanto que também é comum a utilização do método STL de decomposição.
Para uma introdução e mais informações sobre os métodos veja Hyndman e Athanasopoulos (2021).
Gráfico de FAC e FACP
A análise de correlação em séries temporais tem particularidades interessantes: é possível analisar a correlação entre duas ou mais séries temporais e também a correlação entre os valores passados de uma única série. No segundo caso, chamamos esse tipo de análise de autocorrelação, onde o objetivo é mensurar a relação linear entre os valores passados da própria série.
Em termos práticos, as funções de autocorrelação (FAC) e autocorrelação parcial (FACP) servem para mensurar essa relação dentro de uma série temporal. A principal utilidade desta medida é a definição dos termos auto-regressivos (pelo gráfico da FACP) e de média móvel (pelo gráfico da FAC) em modelos ARIMA, quando a finalidade é previsão. Também é possível analisar a característica sazonal da série temporal ao visualizar a medida de autocorrelação em um gráfico.
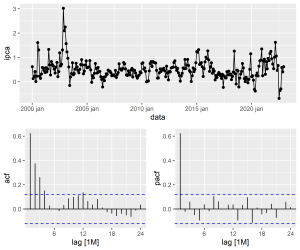
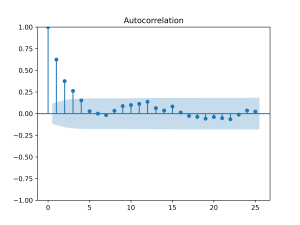
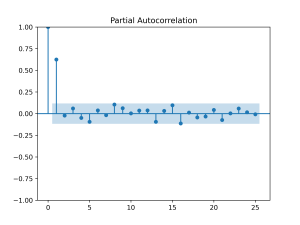
Abaixo exemplificamos como gerar os gráficos da FAC e FACP para a série temporal Índice Nacional de Preços ao Consumidor Amplo (IPCA). Os dados são mensais, de janeiro de 2000 a dezembro de 2022, a unidade de medida é variação % e a fonte é o IBGE.
R
Código
Python
Código
Código
Analisando os gráficos de autocorrelação (FAC e FACP), podemos observar que:
- A sazonalidade da série se traduz em valores maiores de autocorrelação na sazonalidade da série (início/fim de ano), conforme o gráfico da ACF;
- O pico significativo no gráfico da FACP sugere que a série pode seguir uma estrutura de um AR(1) ou AR(2).
Pode ser válido diferenciar a série temporal, se a mesma for não estacionária, para produzir os gráficos de autocorrelação, possibilitando uma leitura “mais limpa”. Séries temporais sazonais, como a do exemplo, são não estacionárias, portanto nesse caso o procedimento é recomendável.
Conclusão
Neste artigo, apresentamos técnicas e métodos úteis para analisar séries temporais e entender suas características. Mostramos as aplicações e interpretações de cada técnica com exemplos de dados reais, usando as linguagens de programação R e Python.
Saiba mais
Se você se interessa por análise e ciência de dados e quiser adquirir os conhecimentos e habilidades destacados neste artigo, dê uma olhadinha nessa formação especial que a Análise Macro preparou:
E para obter os códigos completos deste exercício e de vários outros, dê uma olhada no Clube AM da Análise Macro, onde publicamos exercícios de ciência de dados toda semana em R e Python.
Referências
Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2023-07-13.
