A regressão logística é um modelo estatístico para inferir a probabilidade de um evento acontecer, em uma escala entre 0 e 1. Trata-se de um modelo de classificação, o que significa que o objetivo é determinar sobre qual categoria uma observação de uma variável Y pertence (por exemplo: masculino/feminino) baseado em determinadas características.
O modelo de regressão logística pode ser usado para, por exemplo:
- Classificar se um email é um spam (1) ou não é um spam (0);
- Classificar se uma economia é desenvolvida (1) ou em desenvolvimento (0);
- Classificar o risco de um cliente pagar um empréstimo (1) ou não pagar um empréstimo (0).
Nesse artigo apresentamos o modelo de regressão logística, focando em problemas de classificação binária. Mostramos a intuição do modelo e sua formulação matemática, além de pontuar as principais aplicações e casos de uso. Ao final, demonstramos um exemplo aplicado à classificação econômica para agrupamento em categorias de países com dados reais, usando as linguagens de programação R e Python.
Esse material tem como referência técnica James et al. (2023) e assume que o leitor possua conhecimento prévio sobre regressão linear.
Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.
O modelo de regressão logística
Nessa seção apresentamos a intuição e a formulação matemática do modelo de regressão logística.
A regressão logística é um modelo estatístico para inferir a probabilidade de um evento acontecer, em uma escala entre 0 e 1. A ideia desse modelo é classificar uma variável dependente Y em determinadas categorias, como masculino/feminino, estimando a probabilidade que uma observação de Y pertença a uma determinada categoria usando um conjunto de variáveis independentes X.
O problema
No caso mais simples, a regressão logística possui uma única variável independente (X). Para entender a intuição desse modelo vamos supor o seguinte problema:
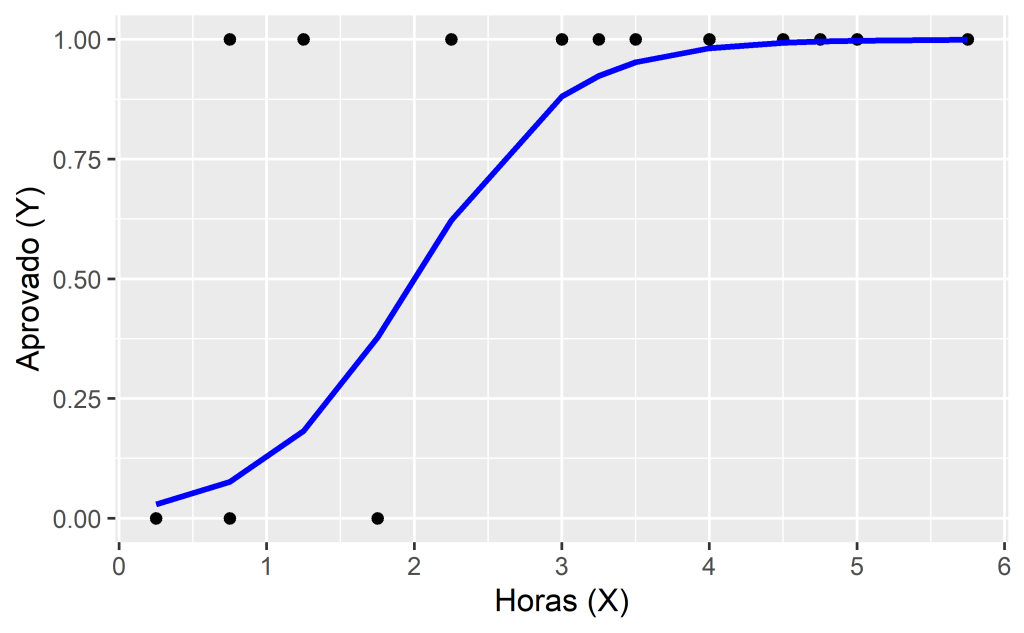
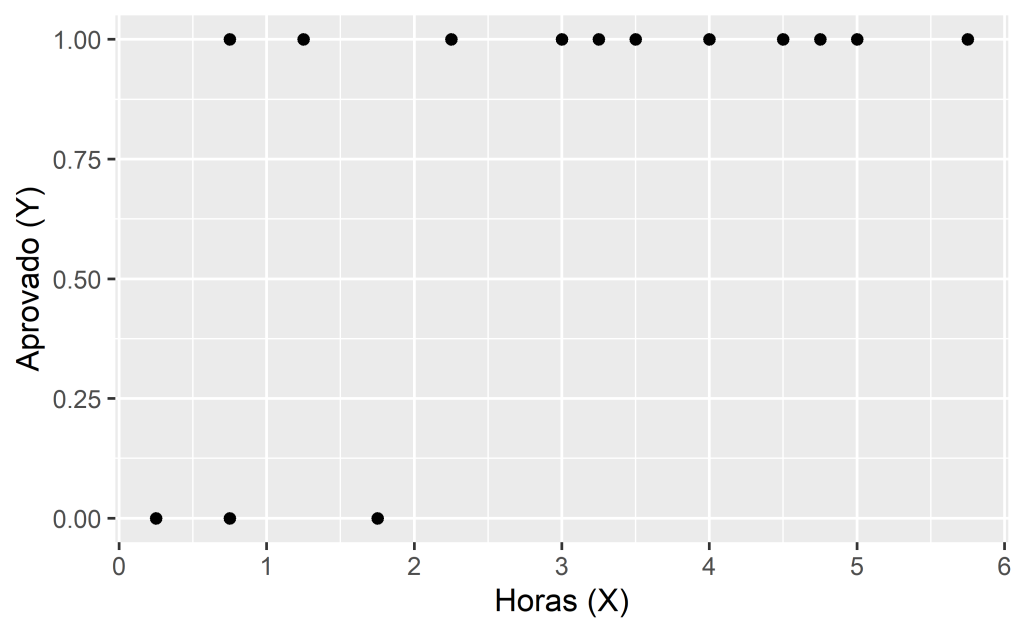
- Um grupo de 20 estudantes gasta entre 0 e 6 horas estudando para passar em uma prova. Deseja-se saber a probabilidade de um estudante passar na prova dado o número de horas estudadas pelo mesmo.
O evento em questão desse problema trata-se de uma variável qualitativa nominal (aprovado ou reprovado, 1 ou 0) e, por isso, o modelo de regressão logística pode ser usado. Se o problema a ser resolvido fosse diferente, como quando se quer prever a nota entre 0 e 10 dado o número de horas estudadas, então uma análise de regressão poderia ser aplicada.
A tabela abaixo apresenta dados sintéticos do problema, mostrando o número de horas estudadas e se o estudante foi aprovado (1) ou reprovado (0):
Queremos estimar a probabilidade do estudante passar na prova (Y = 1) dado o número de horas estudadas (X). Plotando estes dados em um gráfico temos:
Conforme pode ser visto no gráfico, os valores da variável de interesse Y podem ser 0 ou 1, aprovado ou reprovado. Nesse caso, uma tentativa de resolver o problema com uma linha reta de regressão linear seria mal sucedida, pois esse modelo poderia gerar qualquer valor numérico como estimativa para Y.
Devemos usar regressão logística no lugar, pois Y possui uma distribuição de probabilidade de forma que:
O modelo
O modelo de regressão logística utiliza a função logística para converter uma combinação linear de X em uma probabilidade (valor entre 0 e 1). Sendo assim, a função logística tem essa cara:
onde e
são os coeficientes de intercepto e inclinação das probabilidades logarítmicas em função de X. São termos bem conhecidos regressão linear e que aqui estão sofrendo uma transformação logística, por isso o nome do modelo. Essa expressão garante que as estimativas para Y não sejam uma reta, como na regressão linear, mas sim uma função curvilínea.
Fazendo um exercício didático de visualização (assumindo e
com os dados da tabela acima), essa função logística tem esse formato:
Para um dado e
, o termo
(cada ponto na linha azul) é a probabilidade de que o
correspondente seja igual a 1 e
é a probabilidade de que seja igual a 0 (distribuição de Bernoulli).
Estimação do modelo
Queremos encontrar valores constantes de e
que resultam no "melhor ajuste" para os dados. No caso da regressão linear utiliza-se uma função de erro quadrático e o melhor ajuste é obtido minimizando essa função. No caso da regressão logística, utiliza-se a função de probabilidade logarítmica negativa, dada por:
que é equivalente a .
A função de probabilidade logarítmica negativa pode ser interpretada como a "surpresa" do verdadeiro em relação à estimativa
. Ou seja, é a diferença entre duas distribuições de probabilidade, a distribuição estimada
e a distribuição verdadeira
, o que é conhecido também como entropia cruzada. O valor dessa função é sempre maior do que 0 e menor que infinito.
O "melhor ajuste" é obtido através da escolha de valores de e
que minimizam a função de probabilidade logarítmica negativa, o que requer métodos numéricos.
Aplicações do modelo de regressão logística
Nesta seção apresentamos as principais aplicações e casos de uso do modelo de regressão logística.
O modelo de regressão logística é um classificador relativamente simples e bastante útil para uma grande variedade de problemas que podem emergir no mundo real. Além disso, o modelo possui uma interpretação acessível, mesmo para pessoas não técnicas, que é uma probabilidade (%) de determinada variável pertencer a uma determinada categoria com base em determinadas categorias.
Após ter um modelo ajustado, pode-se usar a função logística com novos valores das variáveis independentes para prever a categoria de uma variável de interesse. A agilidade e acessibilidade desse classificador são uns dos pontos positivos em torno do uso da regressão logística, em um mundo onde a informação caminha em um ritmo veloz e há demanda por respostas rápidas.
As principais aplicações e casos de uso da regressão logística são, de acordo com o ChatGPT:
- Classificação Binária: A regressão logística é comumente usada para problemas de classificação binária, onde o objetivo é prever um de dois resultados possíveis (por exemplo, sim/não, spam/não spam, aprovado/reprovado).
- Diagnóstico Médico: A regressão logística pode ser aplicada a diagnósticos médicos, como prever se um paciente tem uma doença específica com base nos resultados de exames médicos e outros fatores.
- Pontuação de Crédito: Bancos e instituições financeiras usam a regressão logística para avaliar a capacidade de crédito de indivíduos, prevendo a probabilidade de inadimplência em um empréstimo.
- Análise de Marketing: A regressão logística é usada em marketing para prever o comportamento do cliente, como a probabilidade de um cliente fazer uma compra ou responder a uma campanha de marketing.
- Previsão de Churn de Clientes: Empresas usam a regressão logística para prever se um cliente provavelmente deixará de usar seus serviços com base em dados históricos e atributos do cliente.
- Atrito de Funcionários: Departamentos de Recursos Humanos podem usar a regressão logística para prever a probabilidade de rotatividade de funcionários com base em diversos fatores, como salário, satisfação no trabalho e tempo de serviço.
- Segmentação de Imagens: Em visão computacional, a regressão logística pode ser usada em tarefas de segmentação de imagem, onde o objetivo é classificar cada pixel em uma imagem em uma das várias categorias.
- Processamento de Linguagem Natural (PLN): A regressão logística pode ser aplicada a tarefas de classificação de texto, como análise de sentimento, detecção de spam e categorização de tópicos.
- Sistemas de Recomendação: A regressão logística pode desempenhar um papel em sistemas de recomendação ao prever se um usuário interage com um item específico (por exemplo, clicar em um link, assistir a um vídeo) com base em seu comportamento e preferências históricas.
- Ciência Política: A regressão logística é usada em ciência política para analisar dados de pesquisas e prever resultados de eleições ou preferências políticas.
- Ciências Ambientais: Cientistas ambientais usam a regressão logística para modelar a probabilidade de ocorrência de um evento, como a presença de uma espécie específica em um habitat com base em variáveis ambientais.
- Controle de Qualidade: A regressão logística pode ser aplicada na fabricação e no controle de qualidade para prever se um produto é defeituoso ou não com base em várias características de qualidade.
- Detecção de Fraudes: A regressão logística pode ajudar a detectar transações fraudulentas ao prever a probabilidade de que uma transação seja fraudulenta com base nos detalhes da transação e em dados históricos.
- Ciências Sociais: A regressão logística é usada em diversas disciplinas das ciências sociais para analisar e prever o comportamento humano, como prever o comportamento de voto, resultados educacionais ou taxas de criminalidade.
- Pesquisa de Mercado: Pesquisadores de mercado usam a regressão logística para entender as preferências do consumidor, o comportamento de compra e a segmentação de mercado.
Percebe-se que as aplicações são várias em diversas áreas, o que pode ser um motivo para a popularidade do modelo atualmente (mesmo que seja simples).
Exemplo de regressão logística: classificação econômica
Nessa seção apresentamos um exemplo do modelo de regressão logística.
O problema que utilizaremos nesse exemplo é o seguinte:
- Deseja-se distinguir os países do mundo, em termos de desempenho econômico, em 2 categorias: economias avançadas (1) e economias não avançadas (0), sendo o último composto por economias de mercados emergentes, de renda média, e de renda baixa.
- A finalidade da classificação é informacional: é mais fácil analisar e comparar o desempenho econômico de países dentro de uma mesma economia, além de servir como insumo para outros tipos de classificação, como, por exemplo, o risco de crédito soberano.
- Em resumo, queremos inferir a probabilidade do país
pertencer a categoria 1 (economias avançadas) ou 0 (economias não avançadas) usando um conjunto de variáveis econômicas (detalhes abaixo).
Os dados utilizados para abordar esse problema são os seguintes:
- Agrupamento econômico do Monitor Fiscal do IMF: consiste de uma classificação oficial, de uma instituição reconhecida internacionalmente, que agrupa os países do mundo em 3 grandes categorias (41 avançadas, 95 emergentes e 59 renda baixa). Esses dados formam a variável de interesse Y do nosso problema de classificação. Essas informações estão disponíveis neste link do IMF, onde há esse outro link para uma planilha de Excel com os agrupamentos e outros metadados.
- Produto Interno Bruto (PIB): consiste na variável utilizada pelo IMF, conforme o Methodological and Statistical Appendix do Monitor Fiscal1, para agrupar as economias pelo tamanho do PIB em dólares americanos. Esses dados, sendo o valor anual de 2018 divulgado para cada país no conjunto de dados WEO a referência aqui utilizada, formam a variável independente X do nosso problema de classificação. Essas informações estão disponíveis na base de dados DBnomics.
Nota: os links acima foram acessados no dia 15/09/2023 e não há garantia de que continuem funcionando no futuro. Contate a fonte da informação para dúvidas.
Os pré-processamentos de dados realizados para a finalidade de classificação via regressão logística são:
- Países emergentes e de baixa renda são agrupados em um grupo “não avançada”;
- Grupos de países são codificados como variável dummy (“avançada” = 1, “não avançada” = 0);
- Países sem informação de PIB para 2019 são tratados como valor ausente e deixados de fora da análise;
- É utilizada a amostragem aleatória estratificada para separar duas amostras: 70% para treino e o restante para teste.
- Valores extremos do PIB, detectados pela regra de corte IQR sugerida por Hyndman e Athanasopoulos (2021), são removidos das amostras;
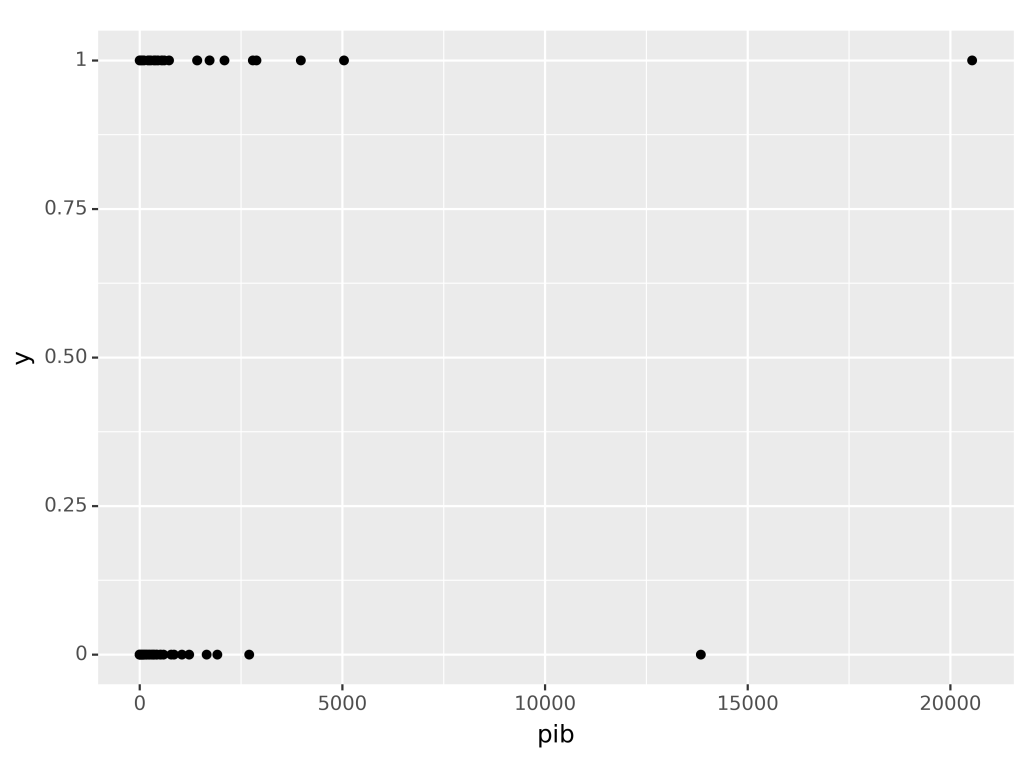
Uma visualização de dados, antes da separação das amostras e remoção de valores extremos, é exibida abaixo:
# Importa bibliotecas
import pandas as pd
import numpy as np
import dbnomics
import plotnine as p9
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
from statsmodels.formula.api import glm
# Carrega dados
dados_brutos_y = pd.read_excel(
io = "https://www.imf.org/external/datamapper/Metadata_Apr2023.xlsx",
sheet_name = "Table A. Economy Groupings",
usecols = "A:C",
nrows = 95
)
dados_brutos_x = dbnomics.fetch_series_by_api_link(
api_link = "https://api.db.nomics.world/v22/series/IMF/WEO:2023-04?" +
"dimensions=%7B%22unit%22%3A%5B%22us_dollars%22%5D%2C%22" +
"weo-subject%22%3A%5B%22NGDPD%22%5D%7D&observations=1",
max_nb_series = 99999
)
# Pré-processamentos
dados_y = (
dados_brutos_y
.rename(
columns = {
"Advanced Economies": "avancada",
"Emerging\nMarket Economies\n": "emergentes",
"Low-Income Developing\nCountries\n": "baixa_renda"
}
)
.melt(var_name = "grupo", value_name = "pais")
.dropna()
.assign(
grupo = lambda x: np.where(x.grupo == "avancada", x.grupo, "nao_avancada"),
y = lambda x: np.where(x.grupo == "avancada", 1, 0)
)
.set_index("pais")
)
dados_x = (
dados_brutos_x
.groupby("weo-country", as_index = False)
.apply(lambda x: x.query("not value.isna()"))
.groupby("weo-country", as_index = False)
.apply(lambda x: x.query("original_period == '2018'"))
.filter(items = ["WEO Country", "value"])
.rename(columns = {"WEO Country": "pais", "value": "pib"})
.reset_index(drop = True)
.set_index("pais")
)
dados = (
dados_y
.join(other = dados_x, on = "pais", how = "left")
.dropna()
.reset_index()
)
# Visualização de dados
print(
p9.ggplot(dados) +
p9.aes(x = "pib", y = "y") +
p9.geom_point()
)
As estimativas do modelo de regressão logística são exibidas abaixo:
# Separação de amostras
dados_treino, dados_teste = train_test_split(
dados,
test_size = 0.3,
random_state = 1984,
stratify = dados.grupo
)
# Função para computar regra de corte IQR
def regra_iqr(x, side):
quantiles = x.quantile([0.25, 0.75])
iqr = quantiles[0.75] - quantiles[0.25]
if side == "lower":
return quantiles[0.25] - 1.5 * iqr
elif side == "upper":
return quantiles[0.75] + 1.5 * iqr
else:
raise Exception("side tem que ser lower ou upper")
y_lower_treino = regra_iqr(dados_treino.pib, 'lower')
y_upper_treino = regra_iqr(dados_treino.pib, 'upper')
y_lower_teste = regra_iqr(dados_teste.pib, 'lower')
y_upper_teste = regra_iqr(dados_teste.pib, 'upper')
# Filtra dados
dados_treino = dados_treino.query("pib > @y_lower_treino and pib < @y_upper_treino")
dados_teste = dados_teste.query("pib > @y_lower_teste and pib < @y_upper_teste")
# Estimação do modelo
modelo = glm("y ~ pib", data = dados_treino, family = sm.families.Binomial()).fit()
modelo.summary()
| Dep. Variable: | y | No. Observations: | 114 |
| Model: | GLM | Df Residuals: | 112 |
| Model Family: | Binomial | Df Model: | 1 |
| Link Function: | Logit | Scale: | 1.0000 |
| Method: | IRLS | Log-Likelihood: | -45.105 |
| Date: | Mon, 18 Sep 2023 | Deviance: | 90.210 |
| Time: | 20:02:29 | Pearson chi2: | 111. |
| No. Iterations: | 5 | Pseudo R-squ. (CS): | 0.04977 |
| Covariance Type: | nonrobust |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
| Intercept | -2.2190 | 0.357 | -6.216 | 0.000 | -2.919 | -1.519 |
| pib | 0.0049 | 0.002 | 2.490 | 0.013 | 0.001 | 0.009 |
O modelo ajustado é o seguinte:
Utilizando esse modelo ajustado para produzir previsões, temos que:
# Produzir estimativas para dados "desconhecidos" probabilidades = ( dados_teste .assign(probabilidade = modelo.predict(dados_teste)) ) probabilidades.head()
pais grupo y pib probabilidade
88 Maldives nao_avancada 0 5.294 0.100360
93 Mongolia nao_avancada 0 13.207 0.103892
16 Ireland avancada 1 385.911 0.415759
37 Taiwan Province of China avancada 1 609.198 0.678495
61 Colombia nao_avancada 0 334.124 0.356100Podemos interpretar esses resultados da seguinte forma: o país Maldives tem probabilidade de 10.036% de pertencer ao grupo “Economias avançadas (1)”.
Note que o modelo atribui uma probabilidade baixa de algumas economias pertencerem ao grupo 1, mesmo que de fato elas pertençam a esse grupo. Erros como esse são esperados em qualquer tarefa de modelagem preditiva, de forma que nossa tarefa é minimizar o erro.
O modelo de regressão logística só entrega estimativas probabilísticas, ou seja, ele não diz sobre qual grupo/categoria as observações pertencem. É convenção converter as probabilidades resultantes do modelo em uma classificação usando um critério de “corte”. Por exemplo: uma probabilidade acima de 50% significa que a observação pertence ao grupo 1 e igual ou inferior a 50% significa que a observação pertence ao grupo 0.
Uma vantagem de aplicar essa classificação a partir das probabilidades geradas pelo modelo de regressão logística é a possibilidade de calcular estatísticas pontuais de acurácia. Dessa forma, é possível verificar como o modelo está errando.
A matriz de confusão é uma maneira simples de analisar o desempenho do modelo. Ela funciona da seguinte forma:
- Colocamos em uma tabela as classificações observadas e as classificações previstas pelo modelo;
- Atribuímos os seguintes rótulos de comparação das classificações:
- VP (verdadeiro positivo): se a classificação prevista e a classificação observada forem iguais a 1;
- FP (falso positivo): se a classificação prevista for igual a 1 e a classificação observada for igual a 0;
- VN (verdadeiro negativo): se a classificação prevista e a classificação observada forem iguais a 0;
- FN (falso negativo): se a classificação prevista for igual a 0 e a classificação observada for igual a 1.
neg_pos = (
probabilidades
.assign(
pred = lambda x: np.where(x.probabilidade > 0.5, 1, 0),
Resultado = lambda x: np.where(
(x.y == 1) & (x.pred == 1), "VP",
np.where(
(x.y == 0) & (x.pred == 1), "FP",
np.where(
(x.y == 0) & (x.pred == 0), "VN",
np.where(
(x.y == 1) & (x.pred == 0), "FN", np.nan
)
)
)
)
)
.assign(Resultado = lambda x: x.Resultado.astype("category"))
.filter(items = ["y", "pred", "Resultado"])
.rename(columns = {"y": "Observada", "pred": "Prevista"})
)
neg_pos.head()
Observada Prevista Resultado
88 0 0 VN
93 0 0 VN
16 1 0 FN
37 1 1 VP
61 0 0 VN- Por fim, sumarizamos a tabela em quantidades de cada resultado em uma matriz 2x2, com a seguinte organização:
| VP | FN |
| FP | VN |
- Com os nossos dados isso é equivalente a:
contagem = neg_pos.Resultado.value_counts()
confusao = pd.DataFrame(
data = {
"Economia Avançada": contagem[["VP", "FP"]].reset_index(drop = True),
"Economia Não Avançada": contagem[["FN", "VN"]].reset_index(drop = True)
}
)
confusao.index = ["Economia Avançada", "Economia Não Avançada"]
confusao
Economia Avançada Economia Não Avançada
Economia Avançada 2 9
Economia Não Avançada 1 40A medida mais simples de avaliação de acurácia do modelo de regressão logística é chamada “acurácia”, que mede a “taxa de acertos” e pode ser calculada da seguinte forma:
Conclusão
Nesse artigo apresentamos o modelo de regressão logística, para resolver problemas de classificação binária. Mostramos a intuição do modelo e sua formulação matemática, além de pontuar as principais aplicações e casos de uso. Ao final, demonstramos um exemplo aplicado à classificação econômica para agrupamento em categorias de países com dados reais, usando as linguagens de programação R e Python.
Quer aprender mais?
- Cadastre-se gratuitamente aqui no Boletim AM e receba toda terça-feira pela manhã nossa newsletter com um compilado dos nossos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas;
- Quer ter acesso aos códigos, vídeos e scripts de R/Python desse exercício? Vire membro do Clube AM aqui e tenha acesso à nossa Comunidade de Análise de Dados;
- Quer aprender a programar em R ou Python com Cursos Aplicados e diretos ao ponto em Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas? Veja nossos Cursos aqui.
Referências
Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2022-04-01.
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical learning with applications in R. 2nd Edition.

![Rendered by QuickLaTeX.com \[\begin{cases}-\ln p_k & \text{ se } Y_k = 1, \\-\ln (1 - p_k) & \text{ se } Y_k = 0\end{cases}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-5568af0cbe168a16787c89504b00eeda_l3.png)