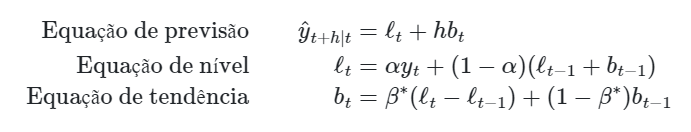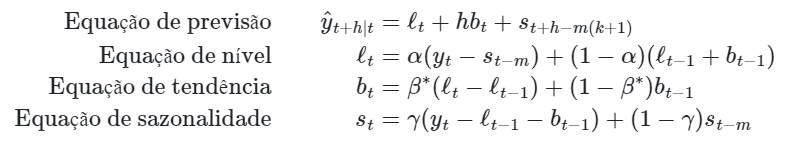Previsão econômica com métodos de Suavização Exponencial

Suavização exponencial é um método para produzir previsões de séries temporais usando médias ponderadas com pesos de observações passadas. O diferencial destes métodos é que as observações mais recentes possuem um peso maior do que as mais antigas, o que tende a produzir previsões mais acuradas.

Nesse texto, apresentamos uma visão geral dos seguintes métodos:

Método de suavização exponencial simples
Método de tendência linear de Holt
Método de tendência linear amortecida
Método de sazonalidade aditiva e multiplicativa de Holt e Winters

Começamos apresentando a mecânica e intuição de cada método e, então, progredimos com a aplicação para previsão de séries temporais da economia do Brasil com distintas e complexas características. São demonstrados exemplos práticos em R e Python.

A referência técnica utilizada é o livro-texto de previsão de séries temporais intitulado “Forecasting: Principles and Practice” de Hyndman e Athanasopoulos (2021).

Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.

Método de suavização exponencial simples

O método de suavização exponencial simples (SES) é, como o nome sugere, o mais simples dos métodos, sendo aplicável a dados sem tendência ou sazonalidade com padrão claro.

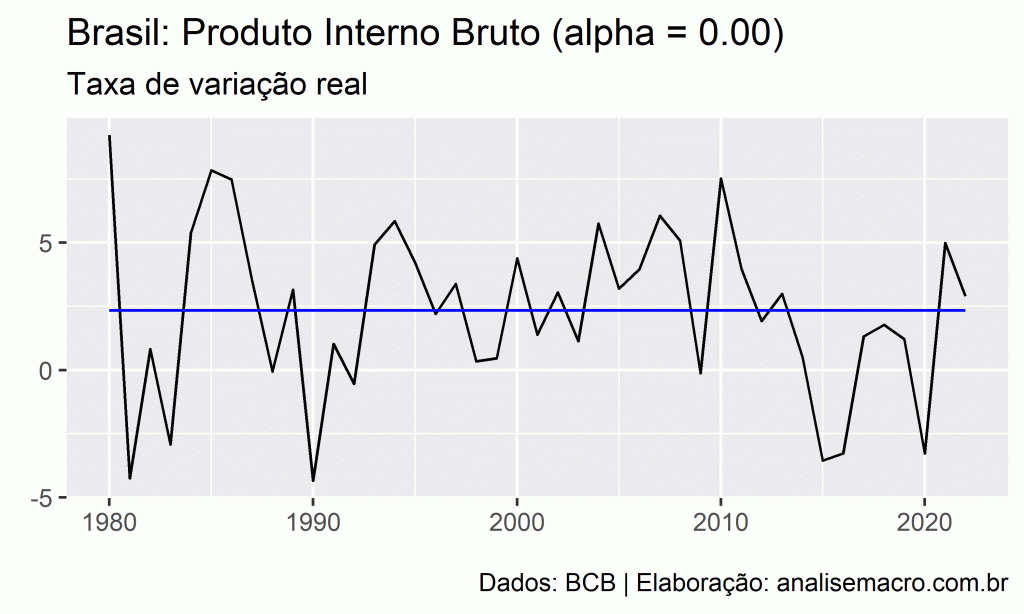
Por exemplo, veja a série do Produto Interno Bruto - Taxa de variação real no ano:

Para modelar e prever essa série sem características de tendência ou sazonalidade claras, poderíamos utilizar o método do passeio aleatório, onde todas as previsões para o futuro são iguais ao último valor observado da série:

$\hat{y}_{T+h|T} = y_{T}$

Dessa forma, o método do passeio aleatório assume que a última observação é a única e mais importante para produzir previsões para a série temporal. Todas as outras observações não possuem importância para prever o futuro. Podemos pensar que esse método é uma média ponderada onde todos os pesos são dados apenas para a última observação.

Outra possibilidade é prever a série temporal com o método da média, onde todas as previsões para o futuro são iguais à média dos dados observados:

$\hat{y}_{T+h|T} = \frac1T \sum_{t=1}^T y_t$

Dessa forma, o método da média assume que todas as observações da série temporal possuem igual importância (pesos) para produzir previsões para o futuro.

Note que estes métodos são dois extremos e, na verdade, queremos um método que é um meio termo. É razoável pensar que pesos maiores devem ser dados para as observações mais recentes do que para observações do passado distante. Esse é o conceito por trás do método de suavização exponencial simples, onde as previsões são geradas utilizando médias ponderadas, onde os pesos decaem exponencialmente (os menores pesos são associados com as observações mais antigas):

$\hat{y}_{T+1|T} = \alpha y_T + \alpha(1-\alpha) y_{T-1} + \alpha(1-\alpha)^2 y_{T-2}+ \cdots$

onde $0 \le \alpha \le 1$ é o parâmetro de suavização que controla a taxa em que os pesos decaem até as observações mais antigas.

A ilustração abaixo retrata esse decaimento do valor de $\alpha$ conforme as observações ficam mais antigas, por isso o método se chama "suavização exponencial":

Note que, conforme andamos para o passado, os pesos sobre as observações ficam próximas de zero muito rapidamente. Se o valor de $\alpha$ for próximo de 1, maiores pesos serão dados para as observações do passado recente, caso contrário, se o valor de $\alpha$ for próximo de 0, maiores pesos serão dados para as observações do passado distante.

Podemos observar como o decaimento exponencial para diferentes valores de $\alpha$ atua sobre dados reais. Tomando como exemplo os dados do PIB e usando a Equação 1 do método de suavização exponencial simples:

O comportamento desse parâmetro é no mínimo interessante, não?

O método SES pode ser representado por essas equações:

A equação de previsão diz que a previsão para o período $t + 1$ é o nível estimado para o período $t$ . A equação de suavização (ou nível) define a estimativa do nível a cada período $t$ .

Note que esse processo precisa iniciar em algum momento, portanto um valor ótimo de início $\ell_0$ e um valor de $\alpha$ precisa ser escolhido.

De forma similar a regressão linear, a escolha dos parâmetros ótimos podem ser feita minimizando a soma dos quadrado dos resíduos.

$\text{SQR}=\sum_{t=1}^T(y_t - \hat{y}_{t|t-1})^2=\sum_{t=1}^Te_t^2$

Em termos de código, podemos estimar o método de suavização exponencial simples e gerar previsões, usando o exemplo de dados do PIB. Abaixo reportamos (a) o sumário do modelo, (b) as métricas de acurácia de treino/teste e (c) o gráfico de valores observados e estimados/previstos dentro da amostra e fora da amostra.

R

Código

Series: pib 
Model: ETS(A,N,N) 
  Smoothing parameters:
    alpha = 0.0001000181 

  Initial states:
     l[0]
 2.817876

  sigma^2:  10.7957

     AIC     AICc      BIC 
211.6478 212.4220 216.3139

.model	.type	ME	RMSE	MAE	MPE	MAPE	MASE	RMSSE	ACF1
ses	Training	0.0004363	3.190418	2.554470	186.73657	325.5248	0.7444242	0.7314324	0.0267742
ses	Test	-2.5553774	3.961013	3.118939	36.85039	112.5396	NaN	NaN	0.0702402

Note que o parâmetro $\alpha$ estimado é aproximadamente zero, por isso a linha reta dentro da amostra. É possível definir o valor do parâmetro manualmente (veja a documentação do pacote).

Python

Código

ETS Results
Dep. Variable:	pib	No. Observations:	35
Model:	ETS(ANN)	Log Likelihood	-90.268
Date:	Fri, 25 Aug 2023	AIC	186.536
Time:	15:23:10	BIC	191.202
Sample:	01-01-1980	HQIC	188.147
	- 01-01-2014	Scale	10.179
Covariance Type:	approx

	coef	std err	z	P>\|z\|	[0.025	0.975]
smoothing_level	0.0001	nan	nan	nan	nan	nan
initial_level	2.8180	0.540	5.217	0.000	1.759	3.877

Ljung-Box (Q):	0.38	Jarque-Bera (JB):	0.52
Prob(Q):	0.83	Prob(JB):	0.77
Heteroskedasticity (H):	0.27	Skew:	-0.29
Prob(H) (two-sided):	0.03	Kurtosis:	2.84

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

RMSE de treino: 3.1904176843135197
RMSE de teste: 3.961092520409291

Note que o parâmetro $\alpha$ estimado é aproximadamente zero, por isso a linha reta dentro da amostra. É possível definir o valor do parâmetro manualmente (veja a documentação do pacote).

A linha preta no gráfico mostra os dados observados, enquanto que as linhas vermelha e azul mostram o ajuste dentro da amostra e a previsão fora da amostra, respectivamente, pelo método SES.

Note que avaliar pontos de previsão sem levar em consideração o intervalo de confiança pode esconder uma grande incerteza e levar a conclusões errôneas.

Método de tendência linear de Holt

Para contemplar séries temporais que apresentam tendência, o método de suavização exponencial de tendência linear de Holt foi desenvolvido.

Por exemplo, veja a série da População do Brasil:

Para modelar e prever essa série com característica de tendência clara, podemos utilizar o método tendência linear de Holt. Esse método possui uma equação de previsão e duas equações de suavização (uma para o nível e outra para a tendência):

onde:

- $\ell_t$ é o nível estimado da série temporal
- $b_t$ é a tendência estimada da série temporal
- $\alpha$ é o parâmetro de suavização para o nível, restrito a $0\le\alpha\le1$
- $\beta^*$ é o parâmetro de suavização para a tendência, restrito a $0\le\beta^*\le1$

Agora a previsão não é mais plana, mas com tendência. A previsão $h$ passos a frente é igual ao último nível estimado mais $h$ vezes a última tendência estimada. Dessa forma, a previsão é uma função linear de $h$ .

Os parâmetros $\alpha$ , $\beta^*$ , $\ell_0$ e $b_0$ devem ser escolhidos de forma a minimizar a SQR.

Em termos de código, podemos estimar o método de tendência linear de Holt e gerar previsões, usando o exemplo de dados da população do Brasil. Abaixo reportamos (a) o sumário do modelo, (b) as métricas de acurácia de treino/teste e (c) o gráfico de valores observados e estimados/previstos dentro da amostra e fora da amostra.

R

Código

Series: pop 
Model: ETS(A,A,N) 
  Smoothing parameters:
    alpha = 0.9999 
    beta  = 0.9990316 

  Initial states:
    l[0]     b[0]
 160.965 2.581412

  sigma^2:  0.0065

      AIC      AICc       BIC 
-34.11905 -29.50366 -29.39685

.model	.type	ME	RMSE	MAE	MPE	MAPE	MASE	RMSSE	ACF1
holt	Training	-0.0456989	0.0718448	0.0507484	-0.0246847	0.0274228	0.0239254	0.0335204	0.1641402
holt	Test	-0.1830038	0.2763105	0.1967748	-0.0858301	0.0925869	NaN	NaN	0.5460862

Note que o parâmetro $\alpha$ estimado é aproximadamente igual a um, o que significa que o nível da série muda rapidamente para capturar a tendência da série. O valor do parâmetro $\beta^*$ estimado também é alto, o que significa que a tendência também muda rapidamente, mesmo que sejam mudanças ligeiras.

Python

Código

ETS Results
Dep. Variable:	pop	No. Observations:	19
Model:	ETS(AAN)	Log Likelihood	23.091
Date:	Fri, 25 Aug 2023	AIC	-36.182
Time:	15:23:16	BIC	-31.460
Sample:	01-01-1996	HQIC	-35.383
	- 01-01-2014	Scale	0.005
Covariance Type:	approx

	coef	std err	z	P>\|z\|	[0.025	0.975]
smoothing_level	0.9999	0.220	4.539	0.000	0.568	1.432
smoothing_trend	0.9998	0.229	4.361	0.000	0.550	1.449
initial_level	160.9720	0.072	2220.538	0.000	160.830	161.114
initial_trend	2.5660	0.102	25.236	0.000	2.367	2.765

Ljung-Box (Q):	1.03	Jarque-Bera (JB):	5.05
Prob(Q):	0.60	Prob(JB):	0.08
Heteroskedasticity (H):	3.41	Skew:	-1.17
Prob(H) (two-sided):	0.16	Kurtosis:	3.98

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

RMSE de treino: 0.07177162542764669
RMSE de teste: 0.2763989469078098

A linha preta no gráfico mostra os dados observados, enquanto que as linhas vermelha e azul mostram o ajuste dentro da amostra e a previsão fora da amostra, respectivamente, pelo método Holt.

Note que avaliar pontos de previsão sem levar em consideração o intervalo de confiança pode esconder uma grande incerteza e levar a conclusões errôneas.

Método de tendência linear amortecida

As previsões pelo método de tendência linear de Holt geram uma tendência constante, seja crescente ou decrescente, indefinidamente para o futuro. É razoável pensar que a população, de qualquer país, não crescerá indefinidamente como prevê o modelo (há um limite físico no mundo) e há evidência empírica que confirma esse raciocínio. Pensando nessa limitação, foi desenvolvido o método de tendência linear amortecida introduzindo um novo parâmetro para “achatar” a linha de tendência para uma linha plana em algum ponto no futuro.

A representação desse método é por três equações, similar ao método de tendência linear de Holt, com a adição de um parâmetro $0<\phi<1$ para amortecer a linha de tendência:

Se o valor de $\phi = 1$ , então esse método é idêntico ao método de tendência linear de Holt. Para valores entre 0 e 1, o parâmetro amortece a linha de tendência para uma linha plana em algum ponto no futuro (pode ser necessário vários passos de previsão para isso acontecer).

Os parâmetros $\alpha$ , $\beta^*$ , $\ell_0$ , $b_0$ e $\phi$ devem ser escolhidos de forma a minimizar a SQR.

Em termos de código, podemos estimar o método de tendência linear amortecida e gerar previsões, continuando o exemplo de dados da população do Brasil. Abaixo reportamos (a) o sumário do modelo e (c) o gráfico de valores observados e previstos fora da amostra.

R

Código

Series: pop 
Model: ETS(A,Ad,N) 
  Smoothing parameters:
    alpha = 0.9999 
    beta  = 0.9998998 
    phi   = 0.9799996 

  Initial states:
     l[0]     b[0]
 160.8795 2.752298

  sigma^2:  0.0033

      AIC      AICc       BIC 
-58.98723 -54.78723 -51.21221

Note que o parâmetro $\phi$ estimado é alto, portanto geramos um período $h = 75$ de previsões para exagerar o efeito e destacar a diferença entre os métodos de tendência linear e tendência amortecida.

Python

Código

ETS Results
Dep. Variable:	pop	No. Observations:	27
Model:	ETS(AAN)	Log Likelihood	35.183
Date:	Fri, 25 Aug 2023	AIC	-60.366
Time:	15:23:21	BIC	-53.887
Sample:	01-01-1996	HQIC	-58.439
	- 01-01-2022	Scale	0.004
Covariance Type:	approx

	coef	std err	z	P>\|z\|	[0.025	0.975]
smoothing_level	0.9999	0.215	4.651	0.000	0.579	1.421
smoothing_trend	0.9998	0.194	5.141	0.000	0.619	1.381
initial_level	160.9720	0.067	2419.246	0.000	160.842	161.102
initial_trend	2.5660	0.093	27.543	0.000	2.383	2.749

Ljung-Box (Q):	1.59	Jarque-Bera (JB):	6.64
Prob(Q):	0.45	Prob(JB):	0.04
Heteroskedasticity (H):	0.84	Skew:	-0.97
Prob(H) (two-sided):	0.80	Kurtosis:	4.46

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

ETS Results
Dep. Variable:	pop	No. Observations:	27
Model:	ETS(AAdN)	Log Likelihood	42.314
Date:	Fri, 25 Aug 2023	AIC	-72.629
Time:	15:23:21	BIC	-64.854
Sample:	01-01-1996	HQIC	-70.317
	- 01-01-2022	Scale	0.003
Covariance Type:	approx

	coef	std err	z	P>\|z\|	[0.025	0.975]
smoothing_level	0.9999	0.286	3.498	0.000	0.440	1.560
smoothing_trend	0.9998	0.520	1.924	0.054	-0.018	2.018
damping_trend	0.9783	0.005	193.879	0.000	0.968	0.988
initial_level	160.9151	0.062	2586.658	0.000	160.793	161.037
initial_trend	2.6809	0.094	28.409	0.000	2.496	2.866

Ljung-Box (Q):	1.96	Jarque-Bera (JB):	7.75
Prob(Q):	0.38	Prob(JB):	0.02
Heteroskedasticity (H):	0.99	Skew:	-0.94
Prob(H) (two-sided):	0.99	Kurtosis:	4.84

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

A linha preta no gráfico mostra os dados observados, enquanto que as demais linhas mostram a previsão fora da amostra pelos método Holt (tendência linear) e Damped Holt (tendência amortecida).

Note que avaliar pontos de previsão sem levar em consideração o intervalo de confiança pode esconder uma grande incerteza e levar a conclusões errôneas.

Método de sazonalidade aditiva e multiplicativa de Holt e Winters

Para contemplar séries temporais que apresentam sazonalidade, o método sazonal de Holt e Winters foi desenvolvido.

Por exemplo, veja a série de Consumo de energia elétrica residencial no Brasil:

Note que parece haver aumento do consumo de energia no verão, caracterizando picos sazonais na série. O método de Holt e Winters possui quatro equações sendo dividido em duas variantes para capturar as características do componente sazonal.

Vamos agora dar uma olhada nas equações destes métodos.

Método de sazonalidade aditiva de Holt e Winters

O método aditivo é preferível quando as variações sazonais são constantes ao longo da série temporal. Nesse caso, o componente sazonal é expresso em valores absolutos na escala dos dados e o nível da série é ajustado sazonalmente subtraindo o componente sazonal.

A representação desse método é dada por quatro equações:

onde:

- $m$ é a periodicidade da sazonalidade da série temporal (i.e., para dados trimestrais $m = 4$ , para mensais $m = 12$ ).
- $k$ é a parte inteira de $(h - 1)/m$ , o que assegura que as estimativas dos índices sazonais utilizadas para previsão são do ano final da amostra.
- $s_t$ é a tendência estimada da série temporal.
- $\gamma$ é o parâmetro de suavização para a sazonalidade, restrito a $0\le\gamma\le 1-\alpha$ .

A equação de nível da série temporal agora tem uma média ponderada entre a série observada ajustada sazonalmente $(y_{t} - s_{t-m})$ e a parte não sazonal da previsão $(\ell_{t-1}+b_{t-1})$ . A equação de tendência é idêntica ao método de tendência linear de Holt. A equação de sazonalidade é uma média ponderada entre o índice sazonal corrente $(y_{t}-\ell_{t-1}-b_{t-1})$ e o índice sazonal da mesma sazonalidade do ano anterior ( $m$ períodos anteriores).

Os parâmetros $\alpha$ , $\beta^*$ , $\ell_0$ , $b_0$ , $\gamma$ e ( $s_0$ , $s_1$ , $s_2$ , $\cdots$ , $s_i$ ) devem ser escolhidos de forma a maximizar a likelihood.

Método de sazonalidade multiplicativa de Holt e Winters

O método multiplicativo é preferível quando as variações sazonais mudam proporcionalmente ao nível da série temporal. Nesse caso, o componente sazonal é expresso em valores relativos (porcentagens) e o nível da série é ajustado sazonalmente dividindo pelo componente sazonal.

A representação desse método é dada por quatro equações:

Os parâmetros $\alpha$ , $\beta^*$ , $\ell_0$ , $b_0$ , $\gamma$ e ( $s_0$ , $s_1$ , $s_2$ , $\cdots$ , $s_i$ ) devem ser escolhidos de forma a maximizar a likelihood.

Em termos de código, podemos estimar o método de Holt e Winters e gerar previsões, usando o exemplo de dados de consumo de energia no Brasil. Abaixo reportamos (a) o sumário dos modelos, (b) as métricas de acurácia de treino/teste e (c) o gráfico de valores observados e previstos fora da amostra.

R

Código

Series: consumo 
Model: ETS(A,A,A) 
  Smoothing parameters:
    alpha = 0.623324 
    beta  = 0.0001000153 
    gamma = 0.0001002009 

  Initial states:
     l[0]     b[0]     s[0]    s[-1]     s[-2]     s[-3]     s[-4]     s[-5]
 5800.234 32.03665 92.20187 100.5172 -20.04147 -215.2619 -375.5736 -477.4777
     s[-6]     s[-7]    s[-8]    s[-9]   s[-10]   s[-11]
 -388.9267 -121.5845 183.5403 333.1145 289.1226 600.3695

  sigma^2:  70303.36

     AIC     AICc      BIC 
3905.546 3908.380 3964.287 
Series: consumo 
Model: ETS(M,A,M) 
  Smoothing parameters:
    alpha = 0.3158006 
    beta  = 0.000115616 
    gamma = 0.2377249 

  Initial states:
     l[0]     b[0]      s[0]    s[-1]     s[-2]     s[-3]     s[-4]     s[-5]
 5859.932 26.44002 0.9958545 1.008129 0.9953057 0.9831547 0.9790915 0.9494972
     s[-6]   s[-7]    s[-8]    s[-9]   s[-10]   s[-11]
 0.9774701 1.00103 1.036292 1.031947 1.000472 1.041757

  sigma^2:  6e-04

     AIC     AICc      BIC 
3836.341 3839.175 3895.082

.model	.type	ME	RMSE	MAE	MPE	MAPE	MASE	RMSSE	ACF1
aditiva	Training	-5.850612	255.9224	189.7507	-0.0986026	2.024241	0.4678438	0.5262880	0.0320122
multiplicativa	Training	8.751134	242.8457	179.5226	0.0372983	1.881044	0.4426256	0.4993966	0.1002884
aditiva	Test	-10.737723	388.4902	315.5402	-0.2158324	2.436667	NaN	NaN	0.1954600
multiplicativa	Test	-242.402599	448.8090	377.8461	-1.9688004	2.957076	NaN	NaN	0.0497196

Note que o parâmetro $\gamma$ com valor baixo no método aditivo indica que o componente sazonal varia pouco ao longo do tempo.

Python

Código

ETS Results
Dep. Variable:	consumo	No. Observations:	234
Model:	ETS(AAA)	Log Likelihood	-1632.919
Date:	Fri, 25 Aug 2023	AIC	3301.838
Time:	15:23:27	BIC	3364.034
Sample:	01-01-2002	HQIC	3326.916
	- 06-01-2021	Scale	67420.012
Covariance Type:	approx

	coef	std err	z	P>\|z\|	[0.025	0.975]
smoothing_level	0.2401	0.048	4.952	0.000	0.145	0.335
smoothing_trend	2.401e-05	nan	nan	nan	nan	nan
smoothing_seasonal	0.3189	0.054	5.873	0.000	0.212	0.425
initial_level	6137.4999	157.749	38.907	0.000	5828.317	6446.683
initial_trend	28.8366	4.441	6.493	0.000	20.133	37.541
initial_seasonal.0	314.2934	178.016	1.766	0.077	-34.612	663.199
initial_seasonal.1	39.6991	169.294	0.234	0.815	-292.112	371.510
initial_seasonal.2	182.3373	172.457	1.057	0.290	-155.672	520.347
initial_seasonal.3	137.1188	173.743	0.789	0.430	-203.411	477.649
initial_seasonal.4	-112.7157	169.625	-0.664	0.506	-445.175	219.743
initial_seasonal.5	-203.5546	170.262	-1.196	0.232	-537.262	130.153
initial_seasonal.6	-301.2631	169.627	-1.776	0.076	-633.726	31.200
initial_seasonal.7	-229.6254	170.409	-1.347	0.178	-563.621	104.371
initial_seasonal.8	-147.3022	172.855	-0.852	0.394	-486.092	191.488
initial_seasonal.9	-72.1107	170.700	-0.422	0.673	-406.677	262.456
initial_seasonal.10	-0.0709	169.105	-0.000	1.000	-331.511	331.369
initial_seasonal.11	0	180.863	0	1.000	-354.485	354.485

Ljung-Box (Q):	72.17	Jarque-Bera (JB):	21.72
Prob(Q):	0.00	Prob(JB):	0.00
Heteroskedasticity (H):	2.60	Skew:	0.53
Prob(H) (two-sided):	0.00	Kurtosis:	4.05

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.
[2] Covariance matrix is singular or near-singular, with condition number 9.23e+16. Standard errors may be unstable.

ETS Results
Dep. Variable:	consumo	No. Observations:	234
Model:	ETS(MAM)	Log Likelihood	-1585.198
Date:	Fri, 25 Aug 2023	AIC	3206.396
Time:	15:23:27	BIC	3268.592
Sample:	01-01-2002	HQIC	3231.473
	- 06-01-2021	Scale	0.001
Covariance Type:	approx

	coef	std err	z	P>\|z\|	[0.025	0.975]
smoothing_level	0.4863	0.077	6.341	0.000	0.336	0.637
smoothing_trend	0.0006	nan	nan	nan	nan	nan
smoothing_seasonal	5.137e-05	nan	nan	nan	nan	nan
initial_level	6137.8849	nan	nan	nan	nan	nan
initial_trend	23.2236	nan	nan	nan	nan	nan
initial_seasonal.0	0.9448	nan	nan	nan	nan	nan
initial_seasonal.1	0.9472	nan	nan	nan	nan	nan
initial_seasonal.2	0.9352	nan	nan	nan	nan	nan
initial_seasonal.3	0.9174	nan	nan	nan	nan	nan
initial_seasonal.4	0.9026	nan	nan	nan	nan	nan
initial_seasonal.5	0.8910	nan	nan	nan	nan	nan
initial_seasonal.6	0.9006	nan	nan	nan	nan	nan
initial_seasonal.7	0.9273	nan	nan	nan	nan	nan
initial_seasonal.8	0.9581	nan	nan	nan	nan	nan
initial_seasonal.9	0.9685	nan	nan	nan	nan	nan
initial_seasonal.10	0.9607	nan	nan	nan	nan	nan
initial_seasonal.11	1.0000	nan	nan	nan	nan	nan

Ljung-Box (Q):	83.67	Jarque-Bera (JB):	14.23
Prob(Q):	0.00	Prob(JB):	0.00
Heteroskedasticity (H):	1.32	Skew:	0.15
Prob(H) (two-sided):	0.22	Kurtosis:	4.17

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

RMSE de treino/aditiva: 259.65363861848385
RMSE de treino/multiplicativa: 231.96693817538554
RMSE de teste/aditiva: 466.6062465949764
RMSE de teste/multiplicativa: 384.74543873532923

Note que o parâmetro $\gamma$ com valor baixo no método multiplicativo indica que o componente sazonal varia pouco ao longo do tempo.

A linha preta no gráfico mostra os dados observados, enquanto que as demais linhas mostram a previsão fora da amostra pelos métodos Holt e Winters com sazonalidade aditiva e multiplicativa.Note que avaliar pontos de previsão sem levar em consideração o intervalo de confiança pode esconder uma grande incerteza e levar a conclusões errôneas.

Conclusão

Neste texto abordamos métodos de suavização exponencial simples, com tendência e com sazonalidade para finalidade de previsão de séries temporais. Mostramos as diferenças de cada método com exemplos de dados econômicos do Brasil, em aplicações nas linguagens de programação R e Python.

Referências

Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2022-04-01.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise de impacto fiscal sobre o dolár com Python

Resultado IBC-br - Outubro/2024

Resultado PMC - Outubro/2024

Como usar Inteligência Artificial para Ler as Atas do COPOM?

Resultado PMS - Outubro/2024

Resultado IPCA - Novembro/2024

Outros artigos relacionados

Análise de impacto fiscal sobre o dolár com Python

Usamos uma cesta de 12 moedas para construir um cenário contrafactual da taxa de câmbio após o último anúncio de pacote fiscal, com base em modelagem Bayesiana. No período, o dolár depreciou quase 5% e passou os R$ 6,15, enquanto que na ausência da intervenção a moeda deveria estar cotada em R$ 5,78.

Resultado IBC-br - Outubro/2024

A Análise Macro apresenta os resultados da IBC-br de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Resultado PMC - Outubro/2024

A Análise Macro apresenta os resultados da PMC de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!