O transporte pode ter grande impacto nos aspectos econômicos de uma localidade, pois permite e expande o acesso das pessoas aos empregos, promove a eficiência e fomenta economias de aglomeração. econômica. Assim, estimaremos o impacto da construção de estações de metrô na renda dos domicílios próximos a elas. Mais especificamente, analisaremos o impacto de três estações de metrô construídas em São Paulo entre 2006 e 2007: Chácara Klabin, Santos-Imigrantes e Alto do Ipiranga.
Conheça o Curso de Avaliação de Políticas Públicas usando o R
Utilizaremos dados dos censos de 1991, 2000 e 2010 com algumas variáveis em nível de setor censitário para a cidade de São Paulo. Para fazer o download dos dados, clique aqui. Existem outras variáveis demográficas/socioeconômicas neste arquivo, mas nesta análise utilizaremos apenas a renda domiciliar per capita, a proporção de apartamentos e a proporção de pessoas com ensino superior.
library(tidyverse) library(MatchIt) library(viridis)
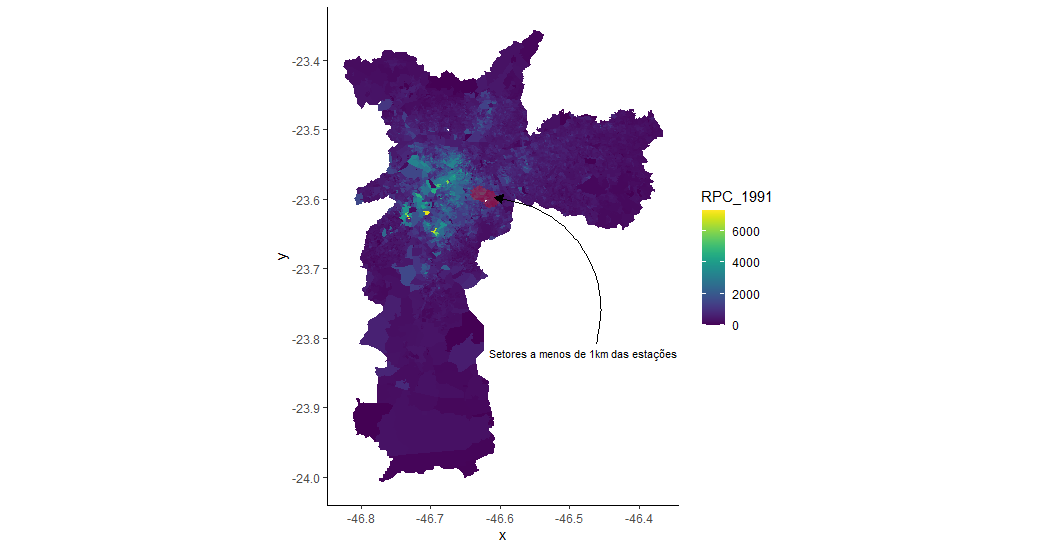
Para fins de definição dos setores censitários tratados, ou seja, que sofreram a intervenção da política pública, estamos considerando a distância de até 1km até a estação construída mais próxima. No mapa a seguir, mostramos como era a renda per capita dos setores censitários de São Paulo em 1991. Os números estão deflacionados e constantes para valores de 2010.
ggplot() + geom_sf(data = df, aes(fill = RPC_1991, geometry = geometry), color = NA) + geom_sf(data = subset(df, df$tratamento == 1), aes(geometry = geometry), color = NA, fill = "red", alpha = 0.3) + theme_classic() + scale_fill_viridis() + geom_curve(data = data.frame(x = -46.4617242682569, y = -23.8093571426162, xend = -46.6083021725803, yend = -23.5976335030379), mapping = aes(x = x, y = y, xend = xend, yend = yend), arrow = arrow(30L, unit(0.1, "inches"), "last", "closed"), inherit.aes = FALSE) + geom_text(data = data.frame(x = -46.4800517493454, y = -23.8206005999123, label = "Setores a menos de 1km das estações"), mapping = aes(x = x, y = y, label = label), size = 2.82, inherit.aes = FALSE)
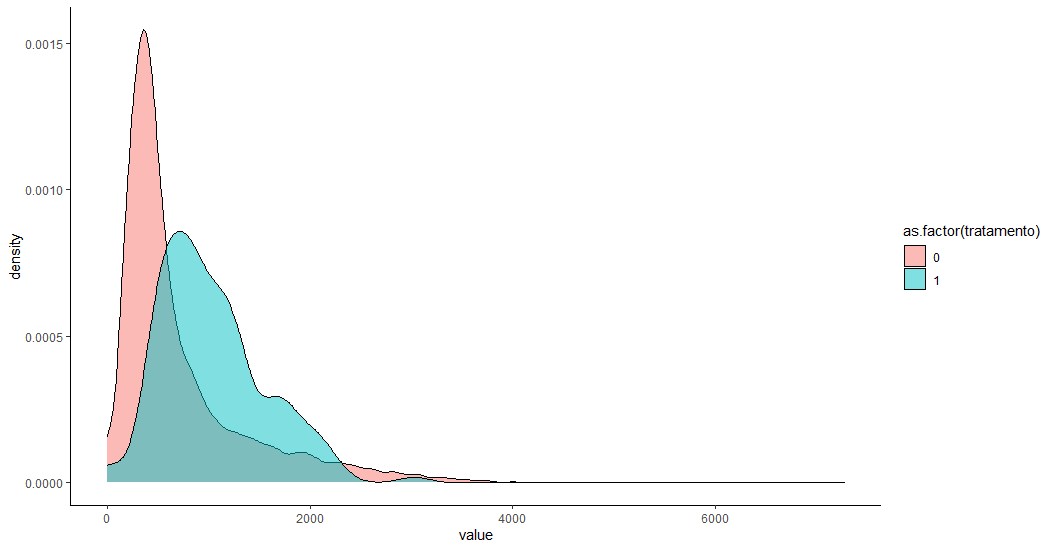
df %>% select(RPC_1991, tratamento) %>% pivot_longer(!tratamento, names_to = "variable", values_to = "value") %>% # mutate(value = scale(value)) %>% ggplot(aes(x = value, fill = as.factor(tratamento))) + geom_density(alpha = .5) + theme_classic()
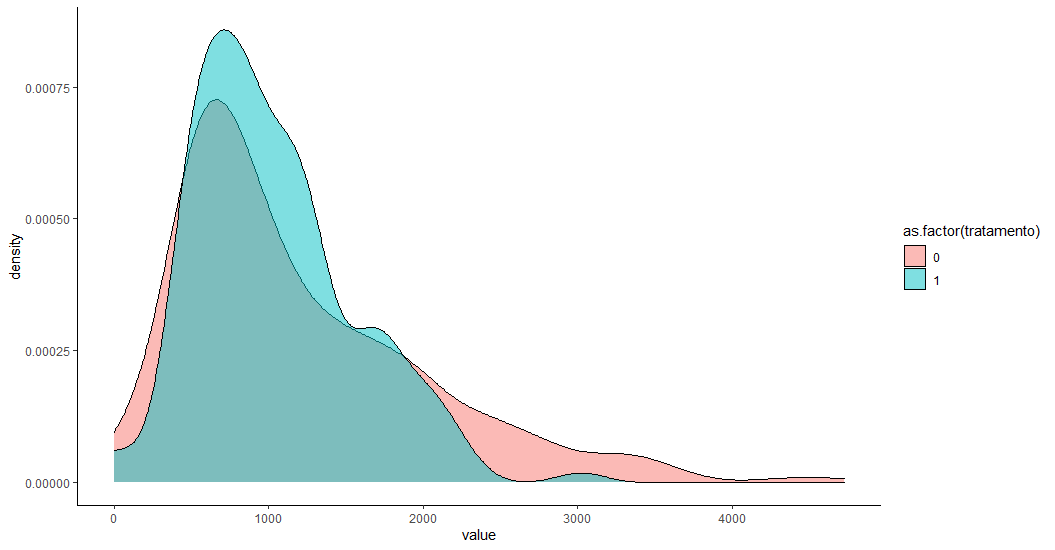
Assim, para avaliar o efeito, é preciso tornar esses grupos semelhantes. Para isso, podemos utilizar técnicas de pareamento, como o Propensity Score Matching, que permite selecionar setores de dentro do grupo restante para formar um grupo de controle parecido com o grupo de tratamento. Além da renda, também utilizamos a proporção de domicílios que são apartamentos, que mede a verticalização do setor censitário, e a proporção de pessoas com ensino superior. O resultado é que a distribuição da renda do grupo de controle fica mais próxima ao setores tratados.
match = matchit(tratamento ~ RPC_1991 + AP_1991 +grad_1991, data = df, method = "nearest", ratio = 3) matched = match.data(match) matched %>% select(RPC_1991, tratamento) %>% pivot_longer(!tratamento, names_to = "variable", values_to = "value") %>% ggplot(aes(x = value, fill = as.factor(tratamento))) + geom_density(alpha = .5)+ theme_classic()
Com isso, podemos estimar o efeito da política pública pelo método de diferenças-em-diferenças. Uma hipótese importante que devemos cumprir para isso é avaliar se a tendência da variável de interesse dos dois grupos era paralela antes do tratamento.
df_reg = matched %>%
select(COD_SET_1991,RPC_1991, RPC_2000, RPC_2010, tratamento) %>%
pivot_longer(!c("COD_SET_1991", "tratamento"),
names_to = c(".value", "ano"),
names_sep = "(_)") %>%
mutate(ano_2010 = ifelse(ano == 2010, 1,0),
pos_tratado = ano_2010*tratamento)
df_reg %>%
group_by(tratamento, ano) %>%
summarise(mean = mean(RPC), n = n()) %>%
ggplot() +
geom_line(aes(x = ano, y = mean, group = tratamento, color = as.factor(tratamento))) +
geom_vline(xintercept = 2) +
theme_classic()
As tendências parecem de fato paralelas no momento anterior ao tratamento. Entretanto, idealmente, deveríamos dispor de mais períodos de tempo anteriores ao tratamento para avaliar se as tendências são de fato paralelas e dar robustez aos resultados.
Assim, estimamos o resultado com uma regressão que utiliza três variáveis binárias, ou dummies. A primeira (tratamento) é igual a 0 quando o setor censitário faz parte do grupo de controle e 1, caso seja do grupo de tratamento. A segunda (ano_2010) equivale a 0 se o período é anterior ao ano de tratamento e 1 se for após o ano de tratamento, no caso 2010. A terceira variável (pos_tratado) é a nossa variável de impacto, que é a interação das duas anteriores, ou seja, se ambas forem igual a 1, essa terá valor 1, caso contrário, 0.
reg_rpc = lm(RPC ~ tratamento + ano_2010 + pos_tratado, data = df_reg) summary(reg_rpc)
O resultado da regressão mostra um impacto de 254 reais das estações na renda domiciliar dos setores censitários próximos, medido pelo valor do parâmetro "pos_tratado".
| Dependent variable: | |
| RPC | |
| tratamento | -186.231** |
| ano_2010 | 836.212*** |
| pos_tratado | 254.091* |
| Constant | 1,385.171*** |
| Observations | 1,656 |
| R2 | 0.135 |
| Residual Std. Error | 1,089.272 (df = 1652) |
| Note: | *p < 0.1; **p < 0.05; ***p < 0.01 |
_______________________
Conheça o Curso de Avaliação de Políticas Públicas usando o R