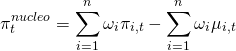Ontem, comentei aqui nesse espaço sobre o cenário benigno para a inflação e como isso estava garantindo uma taxa básica de juros abaixo de 5% no final do ano. Hoje, vou detalhar um pouco melhor esse ponto a partir dos núcleos de inflação. A ideia de um núcleo é capturar a tendência da inflação ao longo do tempo, retirando assim variações idiossincráticas. Em outros palavras, busca capturar a persistência do aumento de preços ao longo do tempo. De modo a ilustrar, considere, por exemplo, que o preço de um bem/serviço varie de acordo com a equação
, onde
representa uma tendência e
uma idiossincracia. Desse modo, para
bens/serviços, o núcleo será dado por:
(1)
Em outras palavras, o objetivo do núcleo é reconhecer e retirar a parte idissiocrática, , concentrando-se na verdadeira tendência da variação dos preços ao longo do tempo. Não à toa, Bancos Centrais de todo o mundo procuram construir e acompanhar medidas de núcleo de inflação. No Brasil, em particular, temos atualmente sete medidas de núcleo. Para uma explicação completa sobre os núcleos de inflação construídos pelo BCB, ver o Estudo Especial 17/2018 Novas Medidas de Núcleos de Inflação.
De modo a ilustrar o comportamento da média desses núcleos ao longo do tempo, bem como comparar com a inflação cheia, vamos criar um gráfico com o comportamento de ambas as séries. Para isso, precisaremos primeiro carregar alguns pacotes, como abaixo.
## Carregar pacotes library(tidyverse) library(readxl) library(sidrar) library(ggplot2) library(forecast) library(tstools) library(scales) library(png) library(grid)
Vamos baixar o número-índice do IPCA a partir do pacote sidrar e posteriormente podemos criar a inflação mensal e a acumulada em 12 meses. O código abaixo implementa.
## Criar Inflação mensal e acumulada em 12 meses ipca_indice = get_sidra(api='/t/1737/n1/all/v/2266/p/all/d/v2266%2013') ipca_indice = ts(ipca_indice$Valor, start=c(1979,12), freq=12) ipca_mensal = round((ipca_indice/stats::lag(ipca_indice,-1)-1)*100,2) ipca_anual = round((ipca_indice/stats::lag(ipca_indice,-12)-1)*100,2)
O número-índice do IPCA tem início em dezembro de 1979, pegando assim toda a hiperinflação da década de 80. Não queremos isso, então pegamos apenas uma amostra dos dados, começando em junho de 2007, quando os choques provenientes da eleição do ex-presidente Lula já haviam se dissipado.
## Criar amostras ipca_indice_subamostra = window(ipca_indice, start=c(2007,06)) ipca_mensal_subamostra = window(ipca_mensal, start=c(2007,06)) ipca_anual_subamostra = window(ipca_anual, start=c(2007,06))
Uma vez que tenhamos a inflação acumulada em 12 meses, vamos agora pegar os núcleos de inflação. Você pode baixar os dados no Sistema de Séries Temporais do Banco Central e depois importar para o R como abaixo. Observe que o código utiliza pipes, de modo já a acumular os dados em 12 meses e se concentrar na amostra que queremos.
## Núcleos
nucleos_12m = read_excel('nucleos.xlsx')[,-1] %>%
ts(start=c(1999,06), freq=12) %>%
acum_p(12) %>%
ts(start=c(1999,06), freq=12) %>%
window(start=c(2007,06))
De posse de todos os dados, podemos agora construir o nosso gráfico com o pacote ggplot2, como no código a seguir.
## Gráfico
media.nucleos = rowMeans(nucleos_12m)
meta = c(rep(4.5, length(media.nucleos)-8), rep(4.25, 8))
time = seq(as.Date('2007-06-01'), as.Date('2019-08-01'), by='1 month')
df = data.frame(time=time, meta=meta, nucleos=round(media.nucleos,2),
inflacao=ipca_anual_subamostra)
img <- readPNG('logo.png')
g <- rasterGrob(img, interpolate=TRUE)
ggplot(df, aes(x=time))+
annotate("rect", fill = "gray", alpha = 0.6,
xmin = as.Date('2016-01-01'),
xmax = as.Date('2019-08-01'),
ymin = -Inf, ymax = Inf)+
geom_line(aes(y=inflacao, colour='Inflação 12 meses'), size=.8)+
geom_line(aes(y=meta, colour='Meta de Inflação'), size=.8)+
geom_line(aes(y=nucleos, colour='Média dos 7 Núcleos'), size=.8)+
scale_colour_manual('',
values=c('Inflação 12 meses'='darkblue',
'Meta de Inflação'='red',
'Média dos 7 Núcleos'='#56B4E9'))+
theme(legend.position = 'top')+
scale_x_date(breaks = date_breaks("1 years"),
labels = date_format("%Y"))+
xlab('')+ylab('% a.a.')+
labs(title='Inflação vs. Núcleos de Inflação',
caption='Fonte: analisemacro.com.br com dados do BCB.')+
theme(panel.background = element_rect(fill='#acc8d4',
colour='#acc8d4'),
plot.background = element_rect(fill='#8abbd0'),
axis.line = element_line(colour='black',
linetype = 'dashed'),
axis.line.x.bottom = element_line(colour='black'),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
legend.position = c(.2,.8),
legend.background = element_rect((fill='#acc8d4')),
legend.key = element_rect(fill='#acc8d4',
colour='#acc8d4'),
plot.margin=margin(5,5,15,5))+
annotation_custom(g,
xmin=as.Date('2016-06-01'),
xmax=as.Date('2019-06-01'),
ymin=8.5, ymax=11)
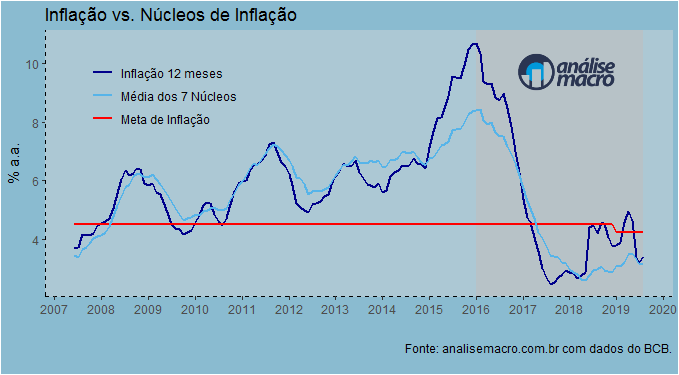
E assim temos um gráfico com o comportamento da inflação cheia e a média dos 7 núcleos construídos e divulgados pelo Banco Central.
Como é possível observar no gráfico acima, a média dos 7 núcleos segue bem comportada na margem - 3,17% no acumulado até agosto -, bem abaixo da meta de inflação para esse ano, que é de 4,25%. Mesmo a inflação cheia também está abaixo da meta e a expectativa, como notei ontem, é que feche próximo a 3,42% no final de 2019. Se os núcleos de inflação forem bons preditores para a inflação no curto prazo - ver, por exemplo, Forecasting inflation in Latin America with core measures, publicado no International Journal of Forecasting - podemos considerar que na ausência de choques relevantes - principalmente, em relação ao câmbio - a inflação tanto esse quanto no próximo ano dá sinais de ficar mesmo abaixo da meta, abrindo caminho para mais cortes na taxa básica de juros nas próximas reuniões do COPOM.
___________________
(*) O script completo do exercício estará disponível logo mais no Clube do Código.
(**) No nosso Curso de Análise de Conjuntura usando o R, nós destrinchamos o IPCA na parte de inflação.