A taxa de câmbio é uma das variáveis mais difíceis de se gerar previsão quantitativa para alguns períodos à frente. Isso porque, são muitas as variáveis domésticas e externas que a influenciam. Não por outro motivo, há uma piada bastante conhecida entre os economistas de que Deus haveria de ter criado o câmbio para humilhá-los. Feita a ressalva, nesse Comentário de Conjuntura apresentamos um modelo de previsão para a taxa de câmbio, que replica o trabalho The unbeatable random walk in exchange rate forecasting: Reality or myth?, proposto por Moosa, I. e K. Burns.
A aula completa e a replicação do modelo, de autoria do nosso Cientista de Dados Fernanda da Silva, estão disponíveis no nosso Curso de Modelos Preditivos aplicados à Macroeconomia.
A especificação do modelo estático é dada abaixo:
(1)
Onde é o log da taxa de câmbio nominal,
é o log da oferta de moeda,
é o log da produção industrial,
é o log(1 + x/100) da taxa de juros,
e
se referem aos países em análise, Brasil e USA, respectivamente.
Já a especificação do modelo dinâmico é dada por:
(2)
Onde e
são as variáveis não observáveis - componentes extraídos de
- tendência e ciclo da variável dependente, respectivamente.
Os modelos são, então, comparados com o benchmark tradicional da literatura representado por um modelo Random Walk, além de outras especificações simples e previsões de agentes de mercado registradas no sistema de expectativas Focus/BCB.
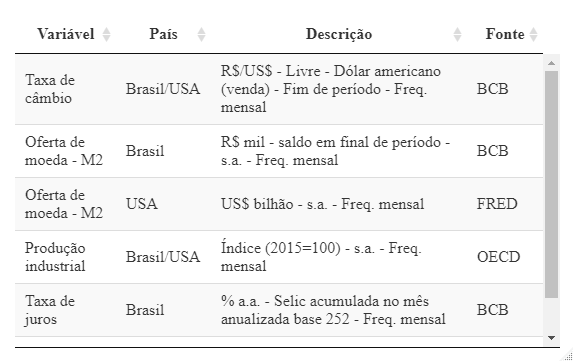
Os dados utilizados são:
O workflow proposto:
1. Obtenção das séries temporais nas bases de dados;
2. Tratamento prévio de dados;
3. Visualização dos dados;
4. Verificar estacionariedade (ADF, PP e KPSS) e aplicar diferenças necessárias, além de transformação logarítmica;
5. Estimação e previsão recursiva do modelo OLS estático e RW, considerando sequência crescente da amostra de dados (amostra inicial com 60 observações);
6. Benchmark com modelo OLS dinâmico (TVP) e expectativas do Focus<sup>1</sup>;
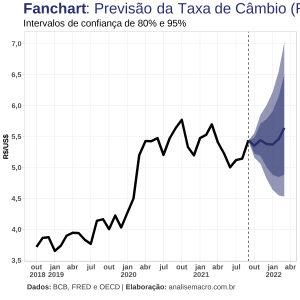
7. Escolha de modelo final e previsão fora da amostra.
O modelo para comparação da capacidade preditiva usado é um OLS TVP. Adicionalmente, comparamos as previsões dos modelos baseline e alternativo com as previsões dos agentes de mercado, reportadas no sistema de expectativas Focus/BCB.
O modelo OLS TVP demonstrou melhor performece, sendo estatisticamente mais acurado em relação a um modelo Random Walk, além de superar o benchmark de mercado (Focus).
_______________
A aula completa com o passo a passo de como replicar o modelo está disponível no Curso de Modelos Preditivos aplicados à Macroeconomia. Os códigos estão disponíveis no Clube AM.