Na próxima quinta-feira, às 20h, eu farei uma aula ao vivo sobre estratégias de previsão da inflação mensal medida pelo IPCA. A aula faz parte do lançamento do nosso novo Curso de Previsão Macroeconométrica usando o R. Para garantir sua presença na aula, coloque seu nome na lista aqui para ser avisado. Nesse Comentário de Conjuntura, a propósito, fazemos um raio-x da inflação brasileira, tendo por foco o IPCA. O código completo está disponível para os membros do Clube AM.
Para começar, nós carregamos os pacotes de R que utilizaremos.
library(tidyverse) library(readxl) library(sidrar) library(forecast) library(tstools) library(scales) library(ggrepel) library(BETS) library(xtable) library(lubridate) library(RcppRoll) library(knitr) library(fpp3) library(xts) library(reshape2) library(rbcb)
Com os pacotes carregados, podemos coletar os dados diretamente do SIDRA/IBGE para o RStudio com o código abaixo. Já aproveito para criar a inflação mensal e a inflação acumulada em 12 meses.
## Criar Inflação mensal e acumulada em 12 meses ipca_indice = '/t/1737/n1/all/v/2266/p/all/d/v2266%2013' %>% get_sidra(api=.) %>% mutate(date = ymd(paste0(`Mês (Código)`, '01'))) %>% select(date, Valor) %>% mutate(mensal = round((Valor/lag(Valor, 1)-1)*100, 2), anual = round((Valor/lag(Valor, 12)-1)*100, 2))
Como o índice pega toda a hiperinflação da década de 80, nós pegamos uma janela a partir de 2007 com o código a seguir.
## Criar amostra
ipca_subamostra = ipca_indice %>%
filter(date >= as.Date('2007-06-01'))
Uma tabela com os últimos resultados é colocada abaixo.
| date | Valor | mensal | anual | |
|---|---|---|---|---|
| 159 | 2020-08-01 | 5357.46 | 0.24 | 2.44 |
| 160 | 2020-09-01 | 5391.75 | 0.64 | 3.14 |
| 161 | 2020-10-01 | 5438.12 | 0.86 | 3.92 |
| 162 | 2020-11-01 | 5486.52 | 0.89 | 4.31 |
| 163 | 2020-12-01 | 5560.59 | 1.35 | 4.52 |
| 164 | 2021-01-01 | 5574.49 | 0.25 | 4.56 |
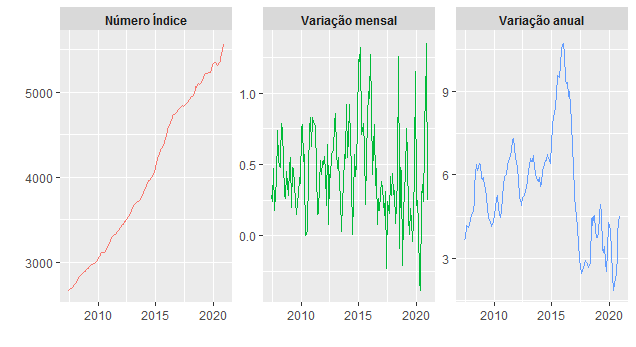
Os gráficos do número índice e da inflação mensal e acumulada em 12 meses são colocados abaixo.
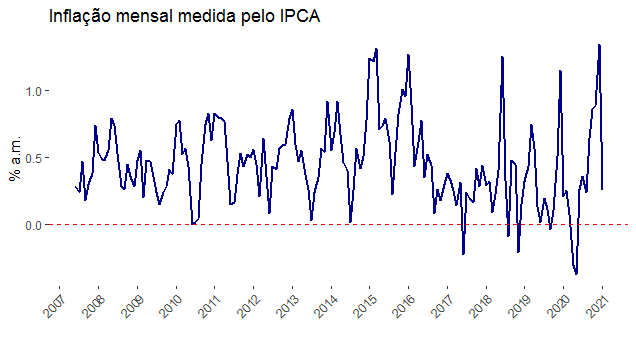
Podemos dar um zoom na inflação mensal, como abaixo.
Uma análise estatística da inflação pode ser feita, a começar pelas estatísticas descritivas do nosso dataset.
| date | Valor | mensal | anual | |
|---|---|---|---|---|
| Min. :2007-06-01 | Min. :2669 | Min. :-0.3800 | Min. : 1.880 | |
| 1st Qu.:2010-10-24 | 1st Qu.:3169 | 1st Qu.: 0.2500 | 1st Qu.: 4.190 | |
| Median :2014-03-16 | Median :3911 | Median : 0.4300 | Median : 5.250 | |
| Mean :2014-03-17 | Mean :4017 | Mean : 0.4522 | Mean : 5.473 | |
| 3rd Qu.:2017-08-08 | 3rd Qu.:4855 | 3rd Qu.: 0.6025 | 3rd Qu.: 6.492 | |
| Max. :2021-01-01 | Max. :5574 | Max. : 1.3500 | Max. :10.710 |
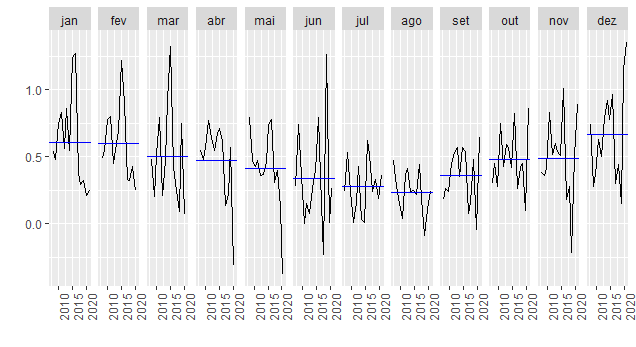
A seguir, podemos ver uma característica bastante conhecida da inflação que é a sua sazonalidade.
A seguir, nós vemos o boxplot e o histograma da inflação mensal medida pelo IPCA.
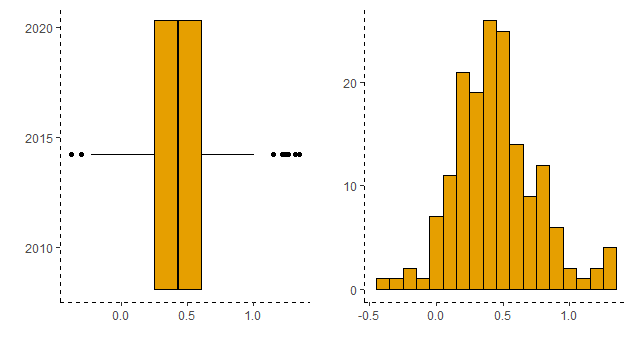
## Pegar núcleos series = c(ipca_ex2 = 27838, ipca_ex3 = 27839, ipca_ms = 4466, ipca_ma = 11426, ipca_ex0 = 11427, ipca_ex1 = 16121, ipca_dp = 16122) nucleos = get_series(series, start_date = '2006-07-01') %>% purrr::reduce(inner_join)
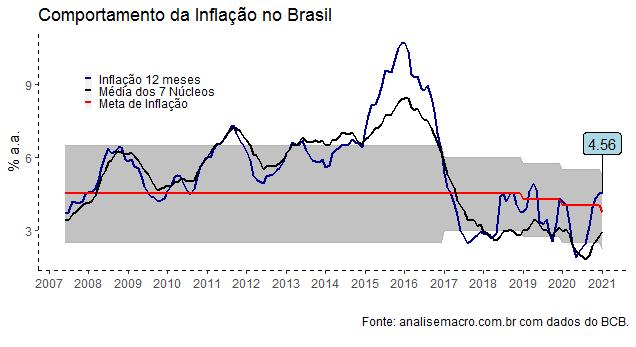
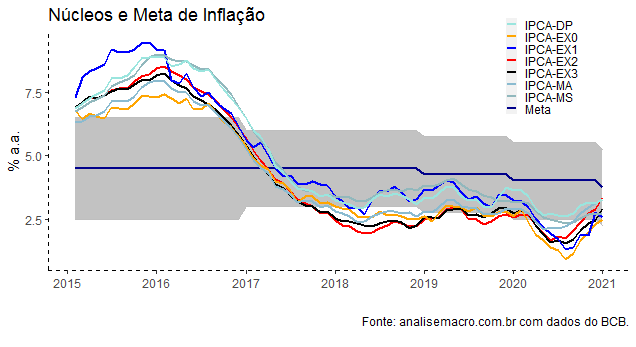
Com os dados dos núcleos disponíveis, nós podemos criar um gráfico como abaixo.
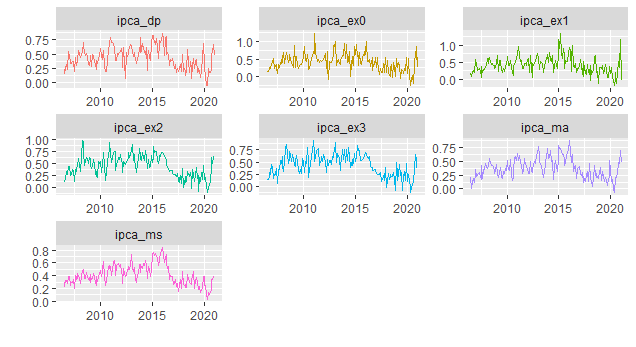
A despeito do avanço da inflação cheia, a média dos sete núcleos do Banco Central ainda se situa abaixo da meta de inflação. A seguir, ilustramos todos os sete núcleos.

Como é possível ver pelo gráfico, todos os sete núcleos situam-se abaixo da meta de inflação, que esse ano é de 3,75%. Na sequência, vemos cada um dos sete grupos, na sua variação mensal.
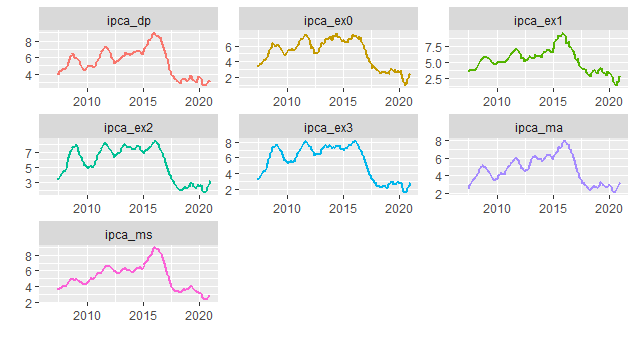
E a variação acumulada em 12 meses.
Os núcleos de inflação são importantes para expurgar choques que ocorrem sobre o índice cheio. O que se vê pelos gráficos acima é que, de fato, os núcleos ainda estão mais comportados do que a inflação cheia, mas na margem, houve sim uma contaminação.
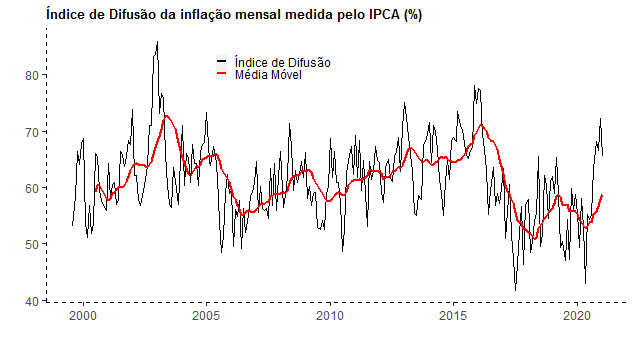
Outra informação importante é a difusão da inflação, isto é, o percentual de subitens que teve variação positiva no mês. Pelo gráfico acima, é possível ver que na margem há um avanço da difusão, já considerando uma média móvel de 12 meses dos dados.
Na sequência, nós podemos ver a contribuição dos 9 grupos para a inflação cheia. Os dados são coletados diretamente do SIDRA/IBGE.
## Baixar e tratar os dados variacao = '/t/7060/n1/all/v/63/p/all/c315/7170,7445,7486,7558,7625,7660,7712,7766,7786/d/v63%202' %>% get_sidra(api=.) %>% mutate(date = parse_date(`Mês (Código)`, format='%Y%m')) %>% select(date, "Geral, grupo, subgrupo, item e subitem", Valor) %>% pivot_wider(names_from = "Geral, grupo, subgrupo, item e subitem", values_from = Valor) peso = '/t/7060/n1/all/v/66/p/all/c315/7170,7445,7486,7558,7625,7660,7712,7766,7786/d/v66%204' %>% get_sidra(api=.) %>% mutate(date = parse_date(`Mês (Código)`, format='%Y%m')) %>% select(date, "Geral, grupo, subgrupo, item e subitem", Valor) %>% pivot_wider(names_from = "Geral, grupo, subgrupo, item e subitem", values_from = Valor) contribuicao = (variacao[,-1]*peso[,-1]/100) %>% mutate(date = variacao$date) %>% select(date, everything())
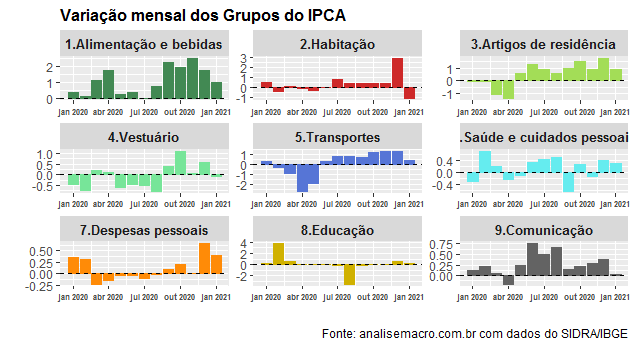
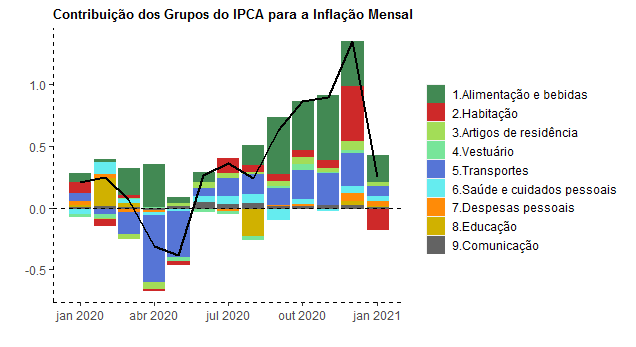
Na sequência, geramos um gráfico com a variação mensal dos nove grupos.
Como se vê, houve um aumento considerável do grupo Alimentação e bebidas ao longo de 2020, o que contribuiu de forma peremptória para o avanço da inflação ao longo daquele ano. Na sequência, colocamos a contribuição de cada um dos grupos para a inflação mensal.
O gráfico acima ilustra a contribuição do grupo Alimentação e bebidas para a inflação mensal ao longo de 2020. A seguir, baixamos as classificações do IPCA diretamente do Banco Central.
series = c('Comercializáveis' = 4447,
'Não Comercializáveis' = 4448,
'Monitorados' = 4449,
'Não Duráveis' = 10841,
'Semi-Duráveis' = 10842,
'Duráveis' = 10843,
'Serviços' = 10844,
'Livres' = 11428)
classificacoes_ipca = get_series(series, start_date = '2007-01-01') %>%
purrr::reduce(inner_join)
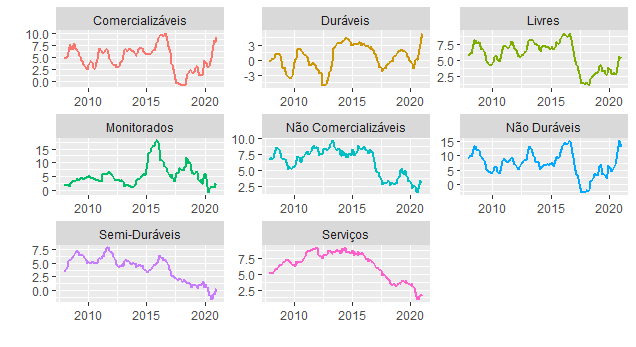
Um gráfico com a variação acumulada em 12 meses é colocado abaixo.
Há uma assimetria entre as classificações do IPCA. Enquanto os preços livres tiveram um avanço nos últimos anos, os monitorados e não comercializáveis seguiram trajetória contrária. Na margem, contudo, essas classificações também mostram algum repique.
Para terminar esse `Raio-x da inflação brasileira`, vamos passar rapidamente pelos Índices Gerais de Preço (IGPs), construídos e divulgados mensalmente pela Fundação Getúlio Vargas. Os (IGPs) são formados por três índices: Índice de Preços por Atacado (IPA), Índice de Preço ao Consumidor (IPC) e Índice Nacional de Custo da Construção Civil (INCC). São divididos por período de coleta em IGP-10, IGP-M e IGP-DI.
Os números-índices do IGP-10, IGP-M e IGP-DI podem ser obtidos aplicando a seguinte fórmula no :
(1)
Onde pode ser 10, M ou DI.
O código a seguir pega os dados diretamente do Banco Central.
series = list('IGP-M'=189, 'IGP-DI'=190, 'IGP-10'=7447, 'IPC-Br'=191,
'INCC'=192, 'IPA'=225)
indices_gerais = get_series(series, start_date = '2007-01-01') %>%
purrr::reduce(inner_join) %>%
gather(variavel, valor, -date)
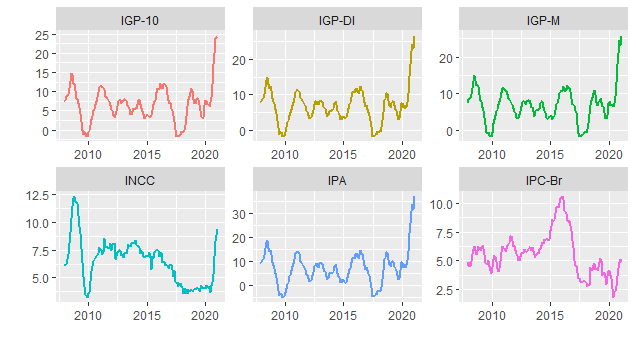
Na sequência, colocamos um gráfico que mostra os índices gerais e seus componentes no acumulado em 12 meses.
Como se vê, houve um salto no IPA, o índice de preços no atacado. Como o mesmo representa 60% dos índices gerais, houve um salto grande nesses índices ao longo de 2020. A tabela abaixo mostra a correlação entre os índices gerais, seus componentes e o IPCA.
| IGP-10 | IGP-DI | IGP-M | INCC | IPA | IPC-Br | IPCA | |
|---|---|---|---|---|---|---|---|
| IGP-10 | 1.0000000 | 0.9839832 | 0.9961309 | 0.4423330 | 0.9714577 | 0.2969412 | 0.3105496 |
| IGP-DI | 0.9839832 | 1.0000000 | 0.9947883 | 0.3984862 | 0.9930553 | 0.2648717 | 0.2771306 |
| IGP-M | 0.9961309 | 0.9947883 | 1.0000000 | 0.4198252 | 0.9855453 | 0.2778136 | 0.2909590 |
| INCC | 0.4423330 | 0.3984862 | 0.4198252 | 1.0000000 | 0.3182797 | 0.4864669 | 0.5081419 |
| IPA | 0.9714577 | 0.9930553 | 0.9855453 | 0.3182797 | 1.0000000 | 0.1571463 | 0.1702913 |
| IPC-Br | 0.2969412 | 0.2648717 | 0.2778136 | 0.4864669 | 0.1571463 | 1.0000000 | 0.9866917 |
| IPCA | 0.3105496 | 0.2771306 | 0.2909590 | 0.5081419 | 0.1702913 | 0.9866917 | 1.0000000 |
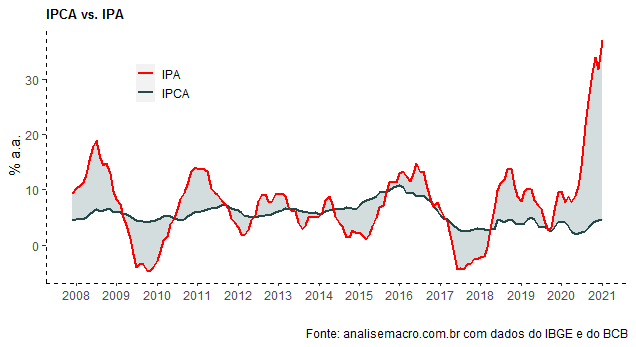
Para terminar, então, mostramos o gap entre o IPA e o IPCA no gráfico abaixo.
_______________________