No post de hoje, mostramos como é possível coletar e analisar os dados da inflação medida pelo IPCA usando o Python.
A inflação é conhecida como o termo que representa a taxa de crescimento do nível geral de preços entre dois períodos distintos. No Brasil, o indicador que consolidou-se como o principal índice de preços é o Índice de Preços ao Consumidor Amplo (IPCA), divulgado pelo IBGE e amplamente utilizado pela autoridade monetária como referência para realizar o controle da inflação.
O IPCA é divulgado mensalmente pelo IBGE, portanto, podemos importar diretamente do SIDRA os dados do indicador utilizando a biblioteca {sidrapy}. Primeiro, iremos buscar a série que diz respeito a variação mensal, acumulada em 3 meses, acumulada em 6 meses, acumulada em 12 meses e acumulado no ano, que diz respeito a tabela 1737.
Em um segundo momento, buscaremos a série de pesos e variação de cada grupo do IPCA, e veremos a contribuição de cada grupo sobre o IPCA, através da tabela 7060.
Para importar as séries com a função get_table do {sidrapy}, buscamos a API das tabelas, com os parâmetros configurados, de forma a obter os códigos. Ensinamos este processo em um post anterior: Coletando dados do SIDRA com o Python.
IPCA Variações
O primeiro passo será buscar a série na plataforma do sidra de forma que possamos resgatar os códigos do parâmetros. Uma vez obtida a API da tabela 1737, e seus respectivos códigos, utilizamos a função get_table para obter a série. Abaixo, os parâmetros e o códigos da API.
/t/1737/n1/all/v/63,69,2263,2264,2265/p/last%20472/d/v63%202,v69%202,v2263%202,v2264%202,v2265%202
# Importa as bibliotecas necessárias !pip install sidrapy import sidrapy import numpy as np import pandas as pd import datetime as dt import seaborn as sns from matplotlib import pyplot as plt
Usamos a função get_table para importar os dados de acordo com os parâmetros da API acima.
# Importa as variações do IPCA
ipca_raw = sidrapy.get_table(table_code = '1737',
territorial_level = '1',
ibge_territorial_code = 'all',
variable = '63,69,2263,2264,2265',
period = 'last%20472')
# Realiza a limpeza e manipulação da tabela
ipca = (
ipca_raw
.loc[1:,['V', 'D2C', 'D3N']]
.rename(columns = {'V': 'value',
'D2C': 'date',
'D3N': 'variable'}
)
.assign(variable = lambda x: x['variable'].replace({'IPCA - Variação mensal' : 'Var. mensal (%)',
'IPCA - Variação acumulada no ano': 'Var. acumulada no ano (%)',
'IPCA - Variação acumulada em 3 meses' : 'Var. MM3M (%)',
'IPCA - Variação acumulada em 6 meses': 'Var. MM6M (%)',
'IPCA - Variação acumulada em 12 meses' : 'Var. MM12M (%)'}),
date = lambda x: pd.to_datetime(x['date'],
format = "%Y%m"),
value = lambda x: x['value'].astype(float)
)
.pipe(lambda x: x.loc[x.date > '2007-01-01']
)
)
# Configura o tema do gráfico
## Cores
colors = ['#282f6b', '#b22200', '#eace3f', '#224f20', '#b35c1e', '#419391', '#839c56','#3b89bc']
## Tamanho
theme = {'figure.figsize' : (15, 10)}
## Aplica o tema
sns.set_theme(rc = theme,
palette = colors)
# Filtra somente para o IPCA acumulado em 12 meses
ipca_12m = (
ipca
.pipe(lambda x: x.loc[x.variable == 'Var. MM12M (%)'])
)
# Plota o IPCA acumulado em 12 meses
sns.lineplot(x = 'date',
y = 'value',
data = ipca_12m).set(title = 'IPCA acumulado em 12 meses',
xlabel = '',
ylabel = '% a.a.')
# Adiciona a fonte no gráfico
plt.annotate('Fonte: analisemacro.com.br com dados do Sidra/IBGE',
xy = (1.0, -0.08),
xycoords='axes fraction',
ha='right',
va="center",
fontsize=10)
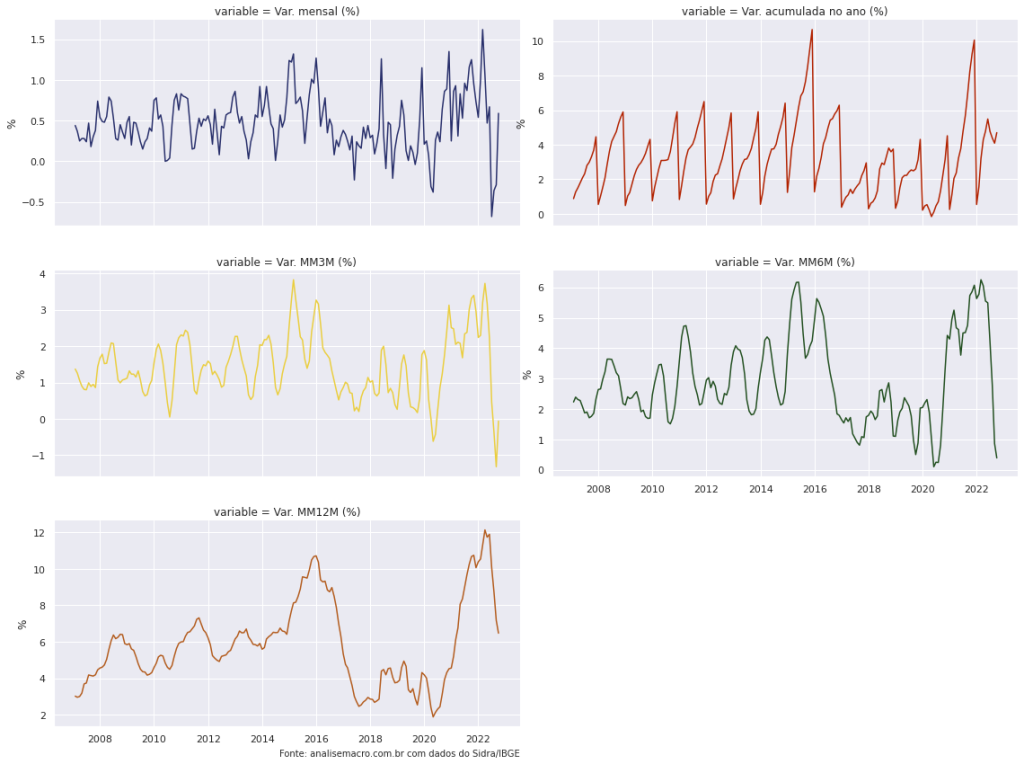
# Plota todas as variações
g = sns.FacetGrid(ipca, col = 'variable',
col_wrap = 2,
hue = 'variable',
sharey = False,
height = 4,
aspect = 2)
g.map_dataframe(sns.lineplot,
x = 'date',
y = 'value').set(xlabel = "",
ylabel = '%')
# Adiciona a fonte no gráfico
plt.annotate('Fonte: analisemacro.com.br com dados do Sidra/IBGE',
xy = (1.0, -0.13),
xycoords='axes fraction',
ha='right',
va="center",
fontsize=10)
IPCA Contribuição por grupo
A contribuição por grupo do IPCA possibilita analisarmos qual grupo possuiu a maior contribuição na variação mensal. A API obtida no SIDRA para a importação da série segue abaixo.
# Importa as variações e os pesos dos grupos do IPCA
ipca_gp_raw = sidrapy.get_table(table_code = '7060',
territorial_level = '1',
ibge_territorial_code = 'all',
variable = '63,66',
period = 'all',
classification = '315/7170,7445,7486,7558,7625,7660,7712,7766,7786'
)
</pre>
# Realiza a limpeza e manipulação da tabela
ipca_gp = (
ipca_gp_raw
.loc[1:,['V', 'D2C', 'D3N', 'D4N']]
.rename(columns = {'V': 'value',
'D2C': 'date',
'D3N': 'variable',
'D4N': 'groups'})
.assign(variable = lambda x: x['variable'].replace({'IPCA - Variação mensal' : 'variacao',
'IPCA - Peso mensal': 'peso'}),
date = lambda x: pd.to_datetime(x['date'],
format = "%Y%m"),
value = lambda x: x['value'].astype(float),
groups = lambda x: x['groups'].astype(str)
)
.pipe(lambda x: x.loc[x.date > '2007-01-01'])
)
# Torna em formato wide e calcula a contribuição de cada grupo pro IPCA
ipca_gp_wider = (
ipca_gp
.pivot_table(index = ['date', 'groups'],
columns = 'variable',
values = 'value')
.reset_index()
.assign(contribuicao = lambda x: (x.peso * x.variacao) / 100)
)
# Importa a biblioteca plotly !pip install plotly import plotly.express as px
# Plota a contribuição de cada grupo com plotly
px.bar(ipca_gp_wider,
x = 'date',
y = 'contribuicao',
color = 'groups',
color_discrete_sequence = colors)
_____________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia