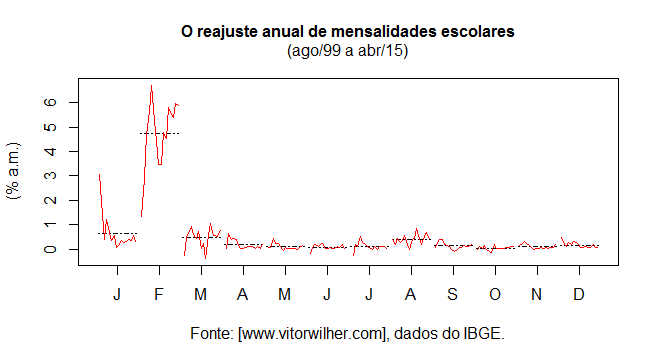
A moça a uma mesa de distância de mim folheia o menu do restaurante. Aos poucos, vai se abrindo para a amiga à sua frente, enquanto dá goles espaçados na taça de água com gás. Como estão caros esses pratos, reclama. "Não é?", concorda a amiga. E começa a repassar os preços do filé com fritas, do Oswaldo Aranha, dos camarões VG e mesmo do talharim salteado na manteiga. É só um macarrão com manteiga, se indigna. Quando a inflação vira tema do almoço, leitor, é por que a coisa está feia, não é mesmo?
Esse é o segundo post [o primeiro aqui] de uma série que tem por objetivos: (i) mostrar, de forma bem introdutória, como lidar com dados macroeconômicos na prática, usando o software R; (ii) entender o comportamento da taxa de variação dos preços no país, bem como gerar alguns modelos de previsão para a inflação, dados seus determinantes. Neste ponto da série falaremos mais detidamente do principal índice de inflação do país: o Índice Nacional de Preços ao Consumidor Amplo (IPCA). Em particular, abordaremos o índice a partir de seus nove grupos.* Vamos, então?
Olhando o dragão por dentro...
O IPCA é construído de forma hierarquizada, sendo dividido em grupos, subgrupos, itens e subitens. Desde agosto de 1999, são nove os grupos: alimentos e bebidas, habitação, artigos de residência, vestuário, transportes, comunicação, saúde e cuidados pessoais, despesas pessoais e educação. O peso de cada um desses grupos no índice cheio é definido mensalmente, de acordo com os gastos das famílias em diferentes bens e serviços. Estes gastos, por sua vez, são captados pela Pesquisa de Orçamento Familiar (POF), também do IBGE - cuja última edição é de 2008-2009.
A cada grupo estarão, então, vinculados subgrupos, itens e subitens. Atualmente, o IPCA possui 373 subitens, distribuídos por 52 itens e 19 subgrupos. Todos os meses, então, o IBGE calculará a variação do preço de cada um desses subitens em relação ao mês anterior, bem como verificará o peso dele no índice cheio. O somatório do produto entre variação mensal e peso de todos os 373 subitens dará a variação mensal do índice cheio. Abaixo um exemplo dessa hierarquia.
Começou a ficar interessante? Bom, então vamos começar a usar o R para a brincadeira ficar mais divertida ainda. Para esse exercício, eu peguei a variação mensal e o peso dos nove grupos do IPCA no SIDRA, para o período de agosto de 2009 a abril de 2015, totalizando 189 observações. Montei minha planilha no Excel com a extensão csv e importei os dados para o R. Dei uma olhada nas primeiras e nas últimas observações das séries com as funções head e tail, para ver se estava tudo ok e pedi os gráficos das variações mensais e, posteriormente, dos pesos dos 9 grupos com o código abaixo. Para usar a função gtsplot, você terá que instalar e carregar o pacote BMR.
## Gráficos das variações mensais e dos pesos
dates <- seq(as.Date('1999-08-01'), as.Date('2015-04-01'), by='1 month')
gtsplot(ipca[,1:9], dates=dates)
gtsplot(ipca[,10:18], dates=dates)
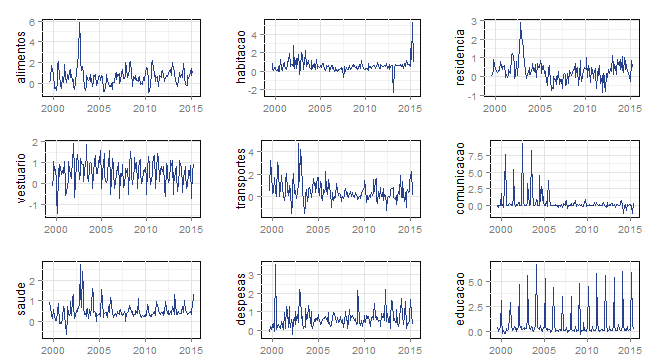
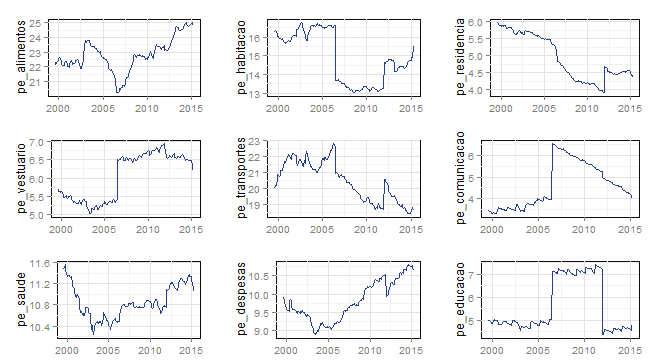
O comportamento da variação mensal não é lá muito interessante, à exceção, talvez, do grupo educação, que mostra uma sazonalidade bem pronunciada e do grupo comunicação que desde 2006 deixou de apresentar justamente essas variações sazonais - que eram fruto dos reajustes previstos nos contratos de privatização da década de 90. O mais interessante, nesse ponto, é observar o comportamento dos pesos desses grupos ao longo do tempo. Observe como o peso do grupo alimentos e bebidas tem aumentado nos últimos anos, assim como o grupo despesas pessoais e saúde e cuidados pessoais. Apenas isso já daria - e dá, acredite - uma boa discussão entre economistas, como, por exemplo, o aumento dos gastos das famílias com serviços ao longo dos últimos anos.
Dos grupos para o índice cheio...
Bom, temos até aqui a variação mensal e o peso dos 9 grupos do IPCA entre agosto de 1999 e abril de 2015. Podemos com esses dados obter a variação mensal do índice cheio de forma simples: pelo somatório do produto entre variação e peso de cada um dos nove grupos. O código abaixo faz exatamente isso.
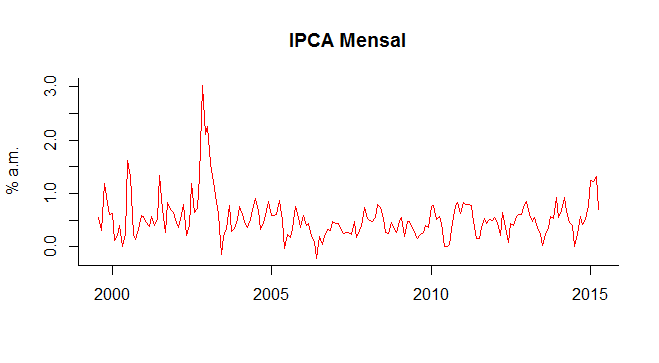
########### Contribuições Mensais para o índice cheio ########### contribuicao <- ipca[,1:9]*ipca[,10:18]/100 colnames(contribuicao) <- colnames(ipca[,1:9]) ##### O IPCA será a soma das contribuições de cada grupo ##### ipcamensal <- ts(round(apply(contribuicao, MARGIN=1, FUN=sum), digits=2), start=c(1999,8), freq=12) plot(ipcamensal, bty='l', col='red', xlab='', ylab='% a.m.', main='IPCA Mensal')
Recapitulando, pegamos a variação mensal e o peso dos 9 grupos do IPCA e, a partir da contribuição de cada um, obtivemos a variação mensal do índice cheio. Você pode, por exemplo, pegar os subitens do IPCA lá no SIDRA, aplicar o mesmo procedimento e obter o índice cheio. Ou subgrupos e itens. Ver, por exemplo, a contribuição de cada subitem dentro de um item, ou dos itens no subgrupo. Enfim, muitas possibilidades para ver o impacto de um determinado bem ou serviço ou um conjunto de bens e serviços no índice cheio.
Com o intuito de começar a fazer uma análise da conjuntura, nós pegamos as últimas seis contribuições mensais dos nove grupos e construímos uma tabela. A ideia é verificar se há algo "saltando" aos olhos - lembre-se do post anterior. Para fazer isso rodamos o código abaixo. A tabela vem logo em seguida.
########### TABELA COM AS CONTRIBUIÇÕES DOS ÚLTIMOS MESES ###########
contribuicao <- tail(round(cbind(ipcamensal,contribuicao), digits=2),
n=6)
contribuicao <- t(contribuicao)
colnames(contribuicao) <- last.mensal
rownames(contribuicao) <- c('IPCA Mensal', 'Alimentos','Habitação',
'Residência', 'Vestuário', 'Transportes',
'Comunicação', 'Saúde',
'Despesas Pessoais', 'Educação')
table.mensal <- stargazer(contribuicao,
title='Contribuição dos 9 grupos para o IPCA (p.p.)',
type='html',
out='contribuicao.html', decimal.mark=',', digits=2,
align=T)
| Nov/15 | Dez/15 | Jan/15 | Fev/15 | Mar/15 | Abr/15 | |
| IPCA Mensal | 0,51 | 0,78 | 1,24 | 1,22 | 1,32 | 0,71 |
| Alimentos | 0,19 | 0,27 | 0,37 | 0,20 | 0,29 | 0,24 |
| Habitação | 0,10 | 0,08 | 0,36 | 0,18 | 0,79 | 0,14 |
| Residência | 0 | 0 | -0,01 | 0,04 | 0,02 | 0,03 |
| Vestuário | 0,03 | 0,06 | -0,04 | -0,04 | 0,04 | 0,06 |
| Transportes | 0,08 | 0,25 | 0,34 | 0,41 | 0,09 | 0,02 |
| Comunicação | 0 | 0 | 0,01 | 0 | -0,05 | 0,01 |
| Saúde | 0,05 | 0,05 | 0,04 | 0,07 | 0,08 | 0,15 |
| Despesas Pessoais | 0,05 | 0,08 | 0,18 | 0,09 | 0,04 | 0,05 |
| Educação | 0,01 | 0 | 0,01 | 0,27 | 0,04 | 0,01 |
Pois é, leitor, nos últimos meses o grupo habitação tem dado uma boa contribuição para a variação mensal do índice cheio. Nesse grupo, está o subitem energia elétrica residencial, que acumula uma variação de 36,3% no primeiro trimestre desse ano. Mas será que é só isso?
E de volta aos grupos: só que agora acumulados em 12 meses...
Como dito acima, a variação mensal dos nove grupos não diz muita coisa sobre o comportamento dos mesmos ao longo do tempo. Para verificar se um determinado grupo tem pressionado mais ou menos o índice cheio, os economistas fazem um "truque": eles acumulam a variação mensal dos últimos 12 meses. Com isso, é possível verificar de uma forma melhor se há ou não pressão ao longo do tempo.
Para fazer isso, é bem simples. Em primeiro lugar, nós tomamos o fator de multiplicação de cada variação percentual mensal e aplicamos o produtório para 12 meses, incluindo o mês em questão. No R, podemos fazer isso ao aplicar o código abaixo.
####### Variações acumuladas em 12 meses dos grupos ######## fator <- (1+(ipca[,1:9]/100)) vanual <- (fator*lag(fator,-1)*lag(fator,-2)*lag(fator,-3)* lag(fator,-4)*lag(fator,-5)*lag(fator,-6)*lag(fator,-7) *lag(fator,-8)*lag(fator,-9)*lag(fator,-10)*lag(fator,-11) -1)*100 colnames(vanual) <- colnames(ipca[,1:9])
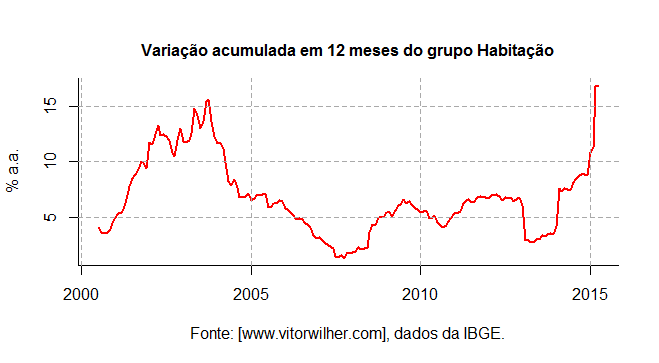
Com o objeto vanual criado, podemos agora aplicar a função gtsplot e obter os gráficos das variações acumuladas em 12 meses dos nove grupos.
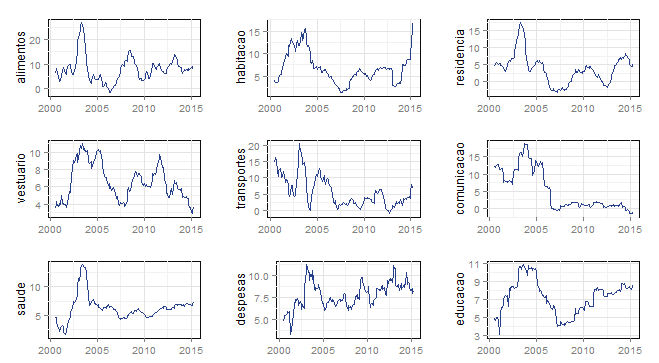
Melhor, não? De fato, o grupo habitação mostra o "salto" notado no primeiro post dessa série, devido ao subitem energia elétrica residencial. Entretanto, é possível verificar uma tendência de alta nos últimos anos no grupo alimentos e bebidas, saúde e cuidados pessoais, despesas pessoais e educação. Para dar números a isso, podemos montar uma tabela com as últimas observações do acumulado em 12 meses desses nove grupos. O código é similar ao da tabela acima.
| Nov/15 | Dez/15 | Jan/15 | Fev/15 | Mar/15 | Abr/15 | |
| IPCA Anual | 6,56 | 6,41 | 7,14 | 7,70 | 8,13 | 8,17 |
| Alimentos | 7,83 | 8,03 | 8,72 | 8,99 | 8,19 | 7,95 |
| Habitação | 8,81 | 8,80 | 10,83 | 11,32 | 16,83 | 16,89 |
| Residência | 6,44 | 5,50 | 4,69 | 4,48 | 4,45 | 4,93 |
| Vestuário | 3,60 | 3,65 | 3,09 | 2,88 | 3,17 | 3,62 |
| Transportes | 4,24 | 3,76 | 5,69 | 8,07 | 7,09 | 6,86 |
| Comunicação | -0,78 | -1,51 | -1,39 | -1,55 | -1,45 | -1,16 |
| Saúde | 6,91 | 6,97 | 6,80 | 6,65 | 6,93 | 7,26 |
| Despesas Pessoais | 8,63 | 8,31 | 8,26 | 8,45 | 7,98 | 8,20 |
| Educação | 8,43 | 8,45 | 8,17 | 8,08 | 8,32 | 8,51 |
A tabela acima nos revela que apenas os grupos vestuário, residência e comunicação estão com valores abaixo da meta de inflação [que é de 4,5% a.a.]. Todos os outros seis possuem valores acima do limite superior de tolerância do regime de metas para a inflação [que é de 6,5% a.a.]. Em outros termos, de fato o grupo habitação tem refletido o reajuste das tarifas de energia elétrica, mas a inflação elevada é um processo bastante consolidado entre os diferentes grupos do IPCA.
É possível, nesse contexto, que essa inflação elevada reflita diferentes categorias de bens ou de serviços? Em outras palavras, será que um determinado grupo de bens ou de serviços está apresentando uma alta mais elevada do que o índice cheio? Além, claro, do problema no setor elétrico? É o que descobriremos no terceiro post dessa série, quando dividiremos o IPCA em preços administrados e livres. Ademais, abriremos os preços livres por comercialização, bem como em bens (duráveis, semi-duráveis e não duráveis) e serviços. Até lá! 🙂
________________________________
(*) O IPCA faz parte do Sistema Nacional de Índices de Preços ao Consumidor (SNIPC), sob coordenação do Instituto Brasileiro de Geografia e Estatística (IBGE), que engloba ainda o Índice Nacional de Preços ao Consumidor (INPC), o IPCA-15 e o IPCA-E. A população-objetivo do IPCA engloba famílias com rendimentos mensais de 1 a 40 salários mínimos e é coletado, em geral, entre os dias 1 e 30 de cada mês.
_______________________________________
Gostou do post? Quer aprender a fazer o mesmo? Dê uma olhada no nosso curso de Introdução ao R com aplicações em Análise de Conjuntura. Faça no Rio de Janeiro ou leve para sua empresa ou universidade!
________________________________________