Verificamos a relação entre o Ibovespa e a variação interanual da Formação Bruta de Capital Fixo (FBCF) por meio do procedimento de Toda-Yamamoto usando o Python como ferramenta.
O procedimento de Toda-Yamamoto
O procedimento Toda-Yamamoto é baseado no conceito de causalidade de Granger, que postula que uma variável X “causa” (no sentido granger) outra variável Y se as informações passadas de X ajudarem a prever melhor Y do que apenas as informações passadas de Y. O teste de Toda-Yamamoto é uma extensão do teste de causalidade de Granger, que leva em consideração a presença de tendências e estruturas não lineares nas séries temporais.
Em caso de não estacionariedade de uma ou mais séries envolvidas no Teste de Granger, é possível que os resultados encontrados sejam espúrios. Nesses casos, um procedimento mais abrangente para ver a relação entre variáveis foi estabelecido na literatura por Toda e Yamamoto (1995). Para ilustrar o procedimento, vamos considerar as séries do Ibovespa e variação interanual da Formação Bruta de Capital Fixo (FBCF).
O procedimento descrito por Toda e Yamamoto (1995) consiste, basicamente, nos seguintes passos:
- Verificar a ordem de integração das variáveis através de testes de raiz unitária e estacionariedade;
- Definir a ordem máxima (m) de integração entre as variáveis;
- Montar o VAR em nível para as variáveis;
- Determinar a ordem de defasagem do VAR(p) pelos critérios de informação tradicionais;
- Ver a estabilidade do modelo, em particular problemas de autocorrelação;
- Se estiver tudo certo, adicionar m defasagens ao VAR, de modo que você terá um VAR(p+m);
- Rodar o teste de Wald com p coeficientes e p graus de liberdade.
Os alunos do curso de Macroeconometria usando o Python, têm a oportunidade de adquirir um conhecimento abrangente em todas as fases do processo, desde a coleta e a preparação dos dados até a análise, o desenvolvimento de modelos econométricos e a comunicação dos resultados, tudo isso utilizando Python como ferramenta principal.
Ibovespa vs. Variação da FBCF no Python
Abaixo, iremos construir um código que permita coletar e tratar os dados do Ibovespa e da FBCF.
Os dados Ibovespa são coletados através do Yahoo Finance via biblioteca yfinance, e referem-se aos pontos do índice de acordo com seu preço de fechamento ajustado do trimestre. A transformação do período é necessária de forma que seja possível comparar com a série da FBCF, visto que esta possui periodicidade trimestral, de acordo com as Contas Nacionais Trimestrais divulgadas pelo IBGE.
Os dados da FBCF, como mencionado, são coletados do IBGE, neste caso, via SIDRA, utilizando a biblioteca sidrapy. Uma vez obtido o índice, é aplicado o cálculo de variação interanual, por meio da equação.
Visualizamos as duas séries e aplicamos o procedimento de Toda-Yamamoto. 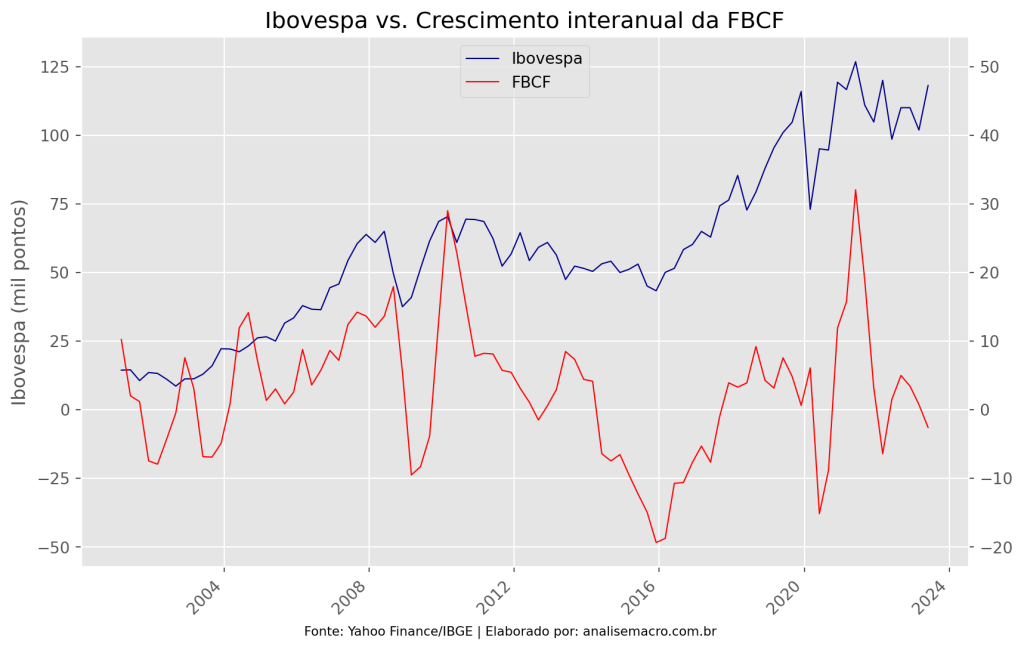
Procedimento Toda-Yamamoto
Estimação do VAR
Neste exercício, vamos pular os dois primeiros passos e prosseguir após o terceiro, em que estimamos diretamente um VAR(2).
Código
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Fri, 10, Nov, 2023
Time: 12:07:09
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: 21.7049
Nobs: 88.0000 HQIC: 21.5031
Log likelihood: -1177.88 FPE: 1.90445e+09
AIC: 21.3670 Det(Omega_mle): 1.66909e+09
--------------------------------------------------------------------
Results for equation dfbcf
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const -0.374502 1.168421 -0.321 0.749
trend -0.371920 0.073667 -5.049 0.000
L1.dfbcf 0.757622 0.096556 7.846 0.000
L1.ibovespa 0.000384 0.000065 5.901 0.000
L2.dfbcf -0.424278 0.085241 -4.977 0.000
L2.ibovespa -0.000053 0.000074 -0.712 0.477
==============================================================================
Results for equation ibovespa
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 2452.573721 1991.389047 1.232 0.218
trend 141.587606 125.553863 1.128 0.259
L1.dfbcf 29.821787 164.564986 0.181 0.856
L1.ibovespa 0.594227 0.110979 5.354 0.000
L2.dfbcf -109.341430 145.279310 -0.753 0.452
L2.ibovespa 0.280096 0.126303 2.218 0.027
==============================================================================
Correlation matrix of residuals
dfbcf ibovespa
dfbcf 1.000000 0.209601
ibovespa 0.209601 1.000000
Posterior a estimação dos modelos, e realizamos um teste de correlação serial dos erros.
O Portmanteau Test é usado para avaliar se existe autocorrelação residual significativa em um modelo ajustado, ou seja, se há dependência linear entre os resíduos em diferentes defasagens.
Se os resíduos são verdadeiramente aleatórios, espera-se que as autocorrelações sejam próximas de zero. O teste calcula uma estatística de teste baseada nas autocorrelações dos resíduos em várias defasagens e a compara com uma distribuição qui-quadrado para determinar se há autocorrelação significativa.
Queremos achar um modelo tal que não rejeite a hipótese nula de ausência de autocorrelação, isto é, não desejamos obter um resultado do p-value do Portmanteau Test menor de 0,05 (5%).
Código
Portmanteau-test for residual autocorrelation. H_0: residual autocorrelation up to lag 16 is zero. Conclusion: reject H_0 at 5% significance level.
========================================
Test statistic Critical value p-value df
----------------------------------------
75.31 74.47 0.044 56
----------------------------------------No momento de verificação do modelo (com novas observações é possível que os resultados se alterem), temos que rejeitamos H0, em um nível próximo de 5%, portanto, continuaremos com o exercício.
Agora vamos verificar a causalidade. Para tanto, utilizamos o Wald test, que é um teste estatístico utilizado para avaliar a significância dos coeficientes estimados em modelos de regressão. Ele é baseado na comparação entre a estimativa do coeficiente e a sua variância estimada.
Para tanto vamos testar a hipótese nula de que um coeficiente é igual a zero. A ideia é verificar se a estimativa do coeficiente é estatisticamente diferente de zero, o que indicaria a presença de um efeito significativo da variável explicativa correspondente sobre a variável resposta.
Se a estatística de teste calculada for maior do que o valor crítico da distribuição qui-quadrado, rejeita-se a hipótese nula, indicando que o coeficiente é significativamente diferente de zero.
Por outro lado, se a estatística de teste for menor do que o valor crítico, não há evidência suficiente para rejeitar a hipótese nula, sugerindo que o coeficiente não é significativamente diferente de zero.
Usaremos o modelo mais parcimonioso: VAR(2). A partir de então, adicionamos m defasagens no modelo, de forma que o valor será 2 + 1, dado que consideramos que uma única diferenciação pode tornar as séries estacionárias (o leitor pode verificar esse caso, tomaremos como dado aqui).
Código
Granger causality Wald-test. H_0: ibovespa does not Granger-cause dfbcf. Conclusion: reject H_0 at 5% significance level.
========================================
Test statistic Critical value p-value df
----------------------------------------
57.90 7.815 0.000 3
----------------------------------------Código
Granger causality Wald-test. H_0: dfbcf does not Granger-cause ibovespa. Conclusion: fail to reject H_0 at 5% significance level.
========================================
Test statistic Critical value p-value df
----------------------------------------
0.8960 7.815 0.826 3
---------------------------------------- Através do exercício, chegamos a conclusão de que o IBOVESPA granger causa DFBCF.Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.


