[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="1_3"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" use_border_color="off" border_color="#ffffff" border_style="solid"]
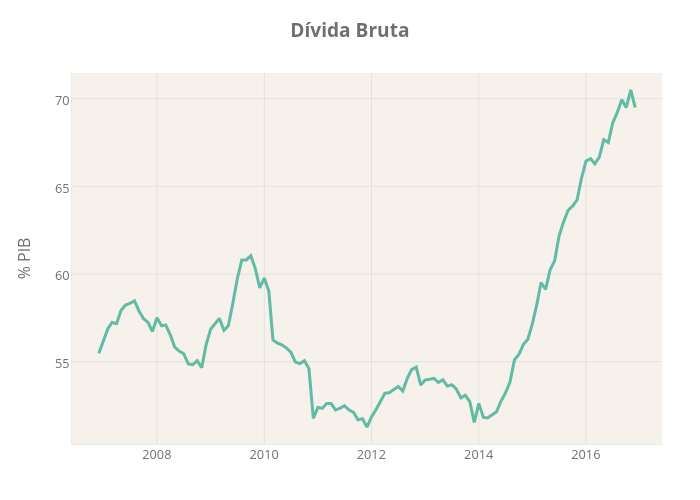
Desde o início de 2014, a Dívida Bruta brasileira tem experimentado uma trajetória de rápida elevação, como pode ser visto no gráfico interativo ao lado. Esse comportamento da dívida, de certo, refletia a enorme incerteza que havia sobre a economia brasileira, de forma geral e sobre o descontrole fiscal, em particular. A ideia é simples. Se o Estado passa a gastar mais do que arrecada, isso sinaliza descontrole fiscal que deve ser financiado por um aumento de dívida pública (ou por emissão monetária, mas isso...). Os agentes que carregam títulos públicos, claro, não são trouxas e pedem mais prêmio para fazer isso, expresso em mais juros. O processo amplifica o aumento inicial da dívida, porque o serviço dela passa a ser mais elevado. E tende a se tornar insustentável se assim for mantido. Simples, não? Bom, até pouco tempo nós não poderíamos quantificar esse aumento de incerteza e sua relação com a dívida pública. Hoje, isso é possível.
[/et_pb_text][/et_pb_column][et_pb_column type="2_3"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="center" use_border_color="off" border_color="#ffffff" border_style="solid"]
[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_button admin_label="Botão" button_url="https://analisemacro.com.br/clube-do-codigo/" url_new_window="off" button_text="Conhecer o Clube do Código" button_alignment="center" background_layout="light" custom_button="off" button_letter_spacing="0" button_use_icon="default" button_icon_placement="right" button_on_hover="on" button_letter_spacing_hover="0"] [/et_pb_button][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" use_border_color="off" border_color="#ffffff" border_style="solid"]
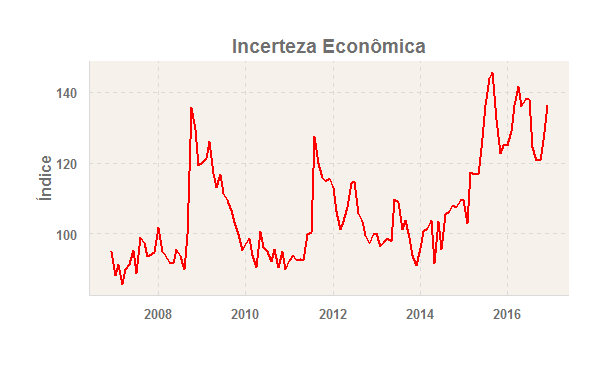
Como já abordei nesse espaço, o IBRE/FGV tem divulgado desde o final do ano passado um Índice de Incerteza Econômica que busca medir essa variável até então abstrata. Iniciativa para outros países pode ser vista aqui. Uma vez que tenhamos esse índice, portanto, é possível verificar a sua relação com diversas variáveis, dentre elas a dívida bruta.
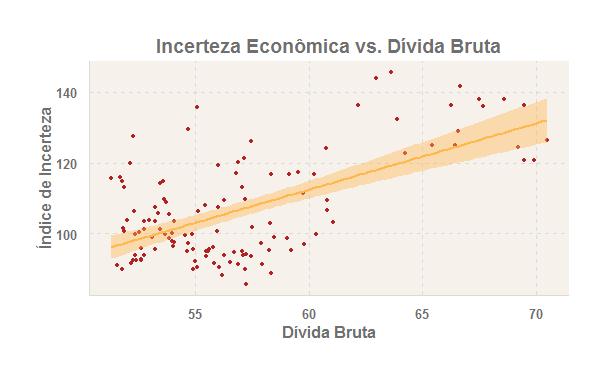
De fato, foi isso que fiz para a Edição 24 do Clube do Código. Minha ideia era não apenas ver como as duas variáveis estão correlacionadas, como pode ser visto no gráfico abaixo, mas também avançar um pouco mais, verificando se existe causalidade nessa relação e se um choque sobre uma variável tem efeito sobre a outra. Para isso, entretanto, eu tive que ter um trabalho um pouco maior, haja visto que as séries não são estacionárias.
[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="Linha"][et_pb_column type="2_3"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" use_border_color="off" border_color="#ffffff" border_style="solid"]
A expectativa, diga-se, era que tanto a dívida afeta a incerteza quanto o contrário também ocorre. Isso porque, o aumento da Dívida sinaliza o quão ruim está o fiscal. Já o aumento da incerteza tende a elevar o prêmio para carregar títulos públicos, o que naturalmente eleva a dívida. Essa intuição inicial acabou sendo confirmada com a aplicação do procedimento de Toda-Yamamoto (1995).
Controlado para o problema de não estacionariedade, o Teste de Granger mostra que existe uma relação bidirecional entre Dívida e Incerteza. Tanto a dívida ajuda a prever a incerteza quanto o contrário também ocorre. Ademais, um choque na Dívida Bruta contribui para elevar a incerteza. Como a série não é estacionária, os choques são incorporados, levando a trajetórias explosivas, mantido, claro, tudo o mais constante. Os membros do Clube do Código receberão o exercício completo, contendo o procedimento de Toda-Yamamoto e a estimação do VEC, na próxima semana. Se você também tiver interesse, clica na figura ao lado e conheça o Clube! Ajude a tornar a blogosfera brasileira cada vez melhor...
[/et_pb_text][/et_pb_column][et_pb_column type="1_3"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2017/02/CLUBE.png" show_in_lightbox="off" url="https://analisemacro.com.br/clube-do-codigo/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="left" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"] [/et_pb_image][/et_pb_column][/et_pb_row][et_pb_row admin_label="Linha"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="left" use_border_color="off" border_color="#ffffff" border_style="solid"]
______________________________
Toda, H. Y. and Yamamoto, T. Statistical inference in vector autoregressions with possibly integrated
process. Journal of Econometrics, 66:225–250, 1995
[/et_pb_text][/et_pb_column][/et_pb_row][/et_pb_section]