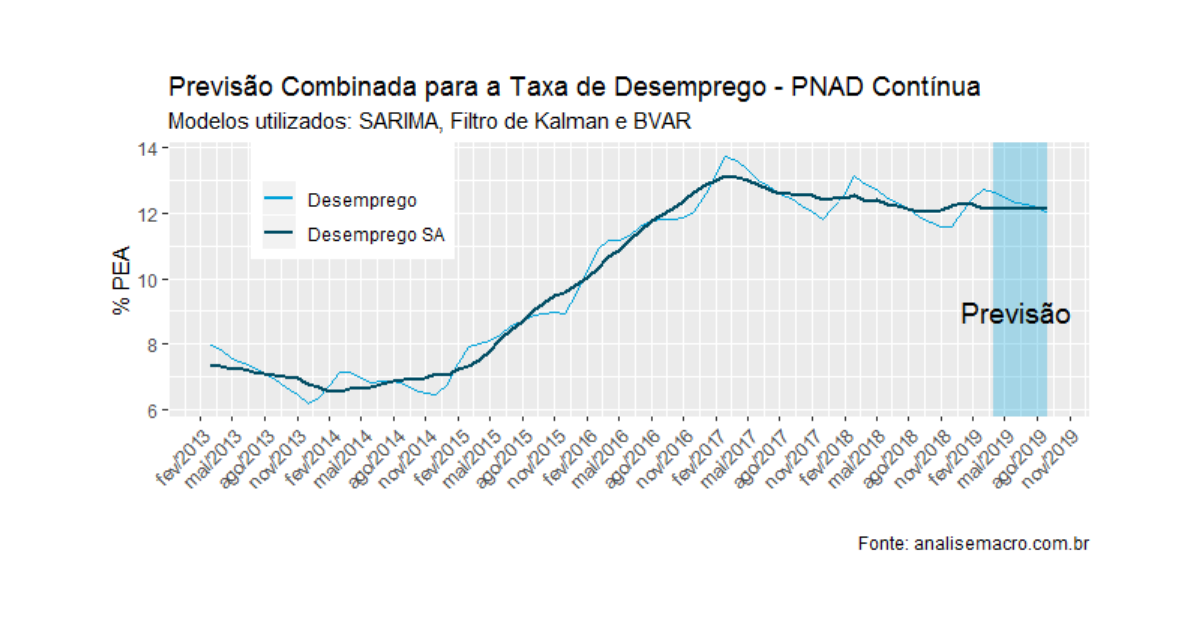
O IBGE divulgou na última terça-feira os resultados da PNAD Contínua para o trimestre móvel encerrado em março. Como comentei no comentário de conjuntura dessa semana, as notícias não foram boas. A taxa de desemprego ficou em 12,7%, enquanto a taxa dessazonalizada ficou em 12%, apenas 0,1 p.p. abaixo de fevereiro. De modo a gerar uma projeção para os próximos seis meses, a propósito, eu atualizei os modelos apresentados na edição 53 do Clube do Código, de modo a gerar uma previsão combinada para a taxa de desemprego.
| SARIMA | Kalman | BVAR | Combinada | |
|---|---|---|---|---|
| 2019 Apr | 12.3 | 12.6 | 12.7 | 12.6 |
| 2019 May | 11.8 | 12.5 | 12.6 | 12.5 |
| 2019 Jun | 11.3 | 12.3 | 12.5 | 12.3 |
| 2019 Jul | 10.9 | 12.3 | 12.4 | 12.3 |
| 2019 Aug | 10.5 | 12.2 | 12.3 | 12.2 |
| 2019 Sep | 10.0 | 12.0 | 12.2 | 12.0 |
A tabela acima resume as previsões geradas pelos três modelos que rodei, bem como a previsão combinada entre eles, com maior peso para o Filtro de Kalman. A taxa de desemprego deve cair dos atuais 12,7% para algo próximo a 12% em setembro. Em termos dessazonalizados, entretanto, a taxa de desemprego deve se manter estável ao longo do período projetado, se mantendo próxima a 12,1%. O gráfico abaixo ilustra.
Caso essas projeções se confirmem, não deixa de ser um banho de água fria...
