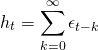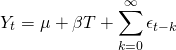Por que estamos demorando tanto para sair da recessão?

[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

Aos poucos e muita lentamente os dados começam a mostrar uma saída da pior recessão da nossa História. O Índice de Atividade Econômica do Banco Central (IBC-Br), divulgado ontem, é um dos indicadores coincidentes que vão nessa direção. Ao incorporar as revisões feitas pelo IBGE nas pesquisa de Comércio e Serviços, o índice mostrou avanço de 1,31% na passagem de janeiro para fevereiro. Na comparação dos três meses terminados em fevereiro com os três meses imediatamente anteriores, houve avanço de 0,76%. A tabela abaixo resume as métricas de crescimento do índice.

[/et_pb_text][et_pb_code admin_label="Código"]<center>   <table border=1> <caption align="bottom"> Variação do IBC-Br (%) </caption> <tr> <th> </th> <th> Mensal </th> <th> Trimestral </th> <th> Interanual </th> <th> 12 meses </th> </tr> <tr> <td align="right"> Dez/16 </td> <td align="right"> -0,09 </td> <td align="right"> -0,33 </td> <td align="right"> -2,33 </td> <td align="right"> -4,55 </td> </tr> <tr> <td align="right"> Jan/17 </td> <td align="right"> 0,62 </td> <td align="right"> 0,13 </td> <td align="right"> 0,51 </td> <td align="right"> -3,88 </td> </tr> <tr> <td align="right"> Fev/17 </td> <td align="right"> 1,31 </td> <td align="right"> 0,76 </td> <td align="right"> -0,73 </td> <td align="right"> -3,56 </td> </tr> </table> </center>[/et_pb_code][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"] Os dados positivos na margem se somam a uma tendência de melhora nas métricas de crescimento ao longo dos últimos meses, como pode ser visto nos gráficos abaixo. [/et_pb_text][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2017/04/ibc.png" show_in_lightbox="on" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"] [/et_pb_image][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

É difícil mover um transatlântico...

Lentamente, vamos aos poucos saindo da recessão. Por que a demora, pode perguntar algum leitor. Bom, a resposta é simples. O PIB é como um transatlântico, que uma vez levado para determinado lado, é difícil mudar a direção. Para ilustrar, mostro aqui um exercício feito no Clube do Código. Considere, para isso, como posto em Licha (2015), que o PIB efetivo possa ser decomposto em duas partes, a saber:

(1) $\begin{equation*}Y_{t} = Y^P_{t} + h_{t} \end{equation*}$

Onde $Y_{t}$ é o PIB em $t$ , $Y^P_{t}$ é a tendência de longo prazo do PIB, chamada de produto potencial e $h_{t}$ é um componente cíclico, chamado de hiato do produto. O PIB Potencial, $Y^P_{t}$ , a tendência do PIB Efetivo ao longo do tempo, reflete condições estruturais da economia, como a população em idade ativa, o estoque de capital, qualidade da educação, qualidade das instituições, etc. O hiato do produto, $h_{t}$ , o componente cíclico, por sua vez, reflete questões conjunturais, como incentivos de política econômica, condições climáticas, choques externos, incertezas políticas, etc.

Em outros termos, no curto prazo o PIB Efetivo pode crescer mais ou menos do que o PIB Potencial, aquela tendência. No longo prazo, entretanto, o crescimento da economia está limitado pela disponibilidade de fatores e pela forma como esses fatores são combinados.

Isto é, supondo que a estrutura da economia possa ser representada por uma função do tipo Cobb-Douglas, com retornos constantes de escala, temos que:

(2) $\begin{equation*}Y_{t} = A_{t} K_{t}^{\alpha_{t}} L_{t}^{1-\alpha_{t}}\end{equation*}$

Onde $K_{t}$ e $L_{t}$ são, respectivamente, a quantidade de capital e trabalho, $A_{t}$ mede a eficiência tecnológica ou a produtividade total dos fatores e $\alpha_{t}$ , por fim, mede a participação do capital na renda nacional.

Nesse contexto, $Y_{t}$ , a soma de bens e serviços finais produzidos em determinado período de tempo, será dado pela combinação entre uma determinada quantidade de estoque de capital com outra de trabalho, moderada pela tecnologia disponível. Em última instância, portanto, $Y_{t}$ estará limitado pela disponibilidade de fatores de produção e pela forma como esses fatores são combinados (a produtividade total dos fatores). Os economistas gostam de chamar essa limitação de produto potencial, ou simplesmente $Y^P_{t}$ .

No curto prazo, a diferença entre $Y_{t}$ e $Y^P_{t}$ será assim dada pelo hiato do produto, $h_{t}$ . O hiato do produto representa assim o que os economistas gostam de chamar de ciclo econômico ou, em outros termos, o ajuste entre o PIB efetivo e o seu potencial. A dinâmica desse ciclo é determinada em grande medida pela rigidez de preços. Fossem os preços totalmente flexíveis, o ajuste seria imediato, implicando que $h_{t}$ seria zero. Nesses termos, para entendermos o tempo desse ajuste, podemos verificar o grau de persistência de um determinado choque sobre o PIB por meio do hiato do produto. Para tanto, como exposto em Licha (2015), vamos considerar que possamos modelar o hiato como um processo autoregressivo de ordem 1, como abaixo:

(3) $\begin{equation*}h_{t} = \alpha h_{t-1} + \epsilon_{t}\end{equation*}$

Onde $\alpha$ é um parâmetro entre 0 e 1 e $\epsilon_{t}$ é supostamente um ruído branco. Fazendo uma iteração de (3), temos que:

$h_{t} = \alpha (\alpha h_{t-2} + \epsilon_{t-1}) + \epsilon_{t}$

(4) $\begin{equation*} h_{t} = \epsilon_{t} + \alpha \epsilon_{t-1} + \alpha^{2} \epsilon_{t-2} + \alpha^{3} \epsilon_{t-3} + ... \end{equation*}$

Nesses termos, a dinâmica do produto será determinada pelo parâmetro $\alpha$ , na medida em que ele explica o grau de persistência de um determinado choque. Em outras palavras, se os choques afetam o PIB somente em um período, não há persistência, de modo que $\alpha$ é igual a zero. O hiato do produto é assim um ruído branco, ou $h_{t} = \epsilon_{t}$ . Considerando que $Y^P_{t}$ possa ser representado por uma tendência determinística e linear, o PIB fica reescrito como

(5) $\begin{equation*} Y_{t} = \mu + \beta T + \epsilon_{t} \end{equation*}$

Se esse for o caso, o processo é descrito como tendência-estacionário. Por outro lado, se $\alpha \neq 0$ , há persistência dos choques, de modo que seus efeitos duram mais do que um período. Considere o caso extremo, em que $\alpha = 1$ . Nesse caso, substituindo em (4), temos que:

(6) $\begin{equation*} h_{t} = \sum_{k=0}^{\infty} \epsilon_{t-k} \end{equation*}$

Ou seja, os choques são totalmente incorporados ao produto. Adicione agora $Y^P_{t}$ , considerando este uma tendência determinística e linear, como em (5). Nesse caso, temos que:

(7) $\begin{equation*} Y_{t} = \mu + \beta T + \sum_{k=0}^{\infty} \epsilon_{t-k} \end{equation*}$

Nesse caso, além dos choques não se dissiparem, a tendência ainda se torna estocástica. Por fim, vamos substituir $Y_{t-1} = \mu + \beta (T-1) + \epsilon_{t-1} + \epsilon_{t-2}...$ de (7), de modo que obtemos:

(8) $\begin{equation*} Y_{t} = \beta + Y_{t-1} + \epsilon_{t} \end{equation*}$

Ou seja, temos um processo autoregressivo de ordem (1), com raiz unitária e drift. No exercício do Clube do Código, ademais, verificamos a partir de um teste de raiz unitária se, de fato, é esse o caso.

Em assim sendo, leitor, uma vez que o PIB tenha sido atingido por um choque capaz de reduzir o investimento em 25%, a reversão desse processo será, naturalmente, demorado. Certo? 🙂

_______________________________________________

Licha, A. L. Teoria da Política Monetária - Uma Abordagem de Nível Intermediário. Editora Alta Books, 2015.

[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="Linha"][et_pb_column type="1_3"][et_pb_button admin_label="Botão" button_url="https://analisemacro.com.br/cursos-de-r/series-temporais/" url_new_window="off" button_text="Curso de Séries Temporais usando o R " button_alignment="center" background_layout="light" custom_button="off" button_letter_spacing="0" button_use_icon="default" button_icon_placement="right" button_on_hover="on" button_letter_spacing_hover="0" /][/et_pb_column][et_pb_column type="1_3"][et_pb_button admin_label="Botão" button_url="https://analisemacro.com.br/clube-do-codigo/" url_new_window="off" button_text="Conhecer o Clube do Código" button_alignment="center" background_layout="light" custom_button="off" button_letter_spacing="0" button_use_icon="default" button_icon_placement="right" button_on_hover="on" button_letter_spacing_hover="0" /][/et_pb_column][et_pb_column type="1_3"][et_pb_button admin_label="Botão" button_url="https://analisemacro.com.br/cursos-de-r/macroeconometria/" url_new_window="off" button_text="Curso de Macroeconometria usando o R " button_alignment="center" background_layout="light" custom_button="off" button_letter_spacing="0" button_use_icon="default" button_icon_placement="right" button_on_hover="on" button_letter_spacing_hover="0" /][/et_pb_column][/et_pb_row][/et_pb_section]

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise de impacto fiscal sobre o dolár com Python

Resultado IBC-br - Outubro/2024

Resultado PMC - Outubro/2024

Como usar Inteligência Artificial para Ler as Atas do COPOM?

Resultado PMS - Outubro/2024

Resultado IPCA - Novembro/2024

Outros artigos relacionados

Análise de impacto fiscal sobre o dolár com Python

Usamos uma cesta de 12 moedas para construir um cenário contrafactual da taxa de câmbio após o último anúncio de pacote fiscal, com base em modelagem Bayesiana. No período, o dolár depreciou quase 5% e passou os R$ 6,15, enquanto que na ausência da intervenção a moeda deveria estar cotada em R$ 5,78.

Resultado IBC-br - Outubro/2024

A Análise Macro apresenta os resultados da IBC-br de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Resultado PMC - Outubro/2024

A Análise Macro apresenta os resultados da PMC de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!