Esse é o terceiro capítulo da série sobre política fiscal que estamos publicando nesse espaço. O objetivo é buscar responder algumas perguntas sobre a situação fiscal brasileira, fazendo uso para isso do
Esse é o terceiro capítulo da série sobre política fiscal que estamos publicando nesse espaço. O objetivo é buscar responder algumas perguntas sobre a situação fiscal brasileira, fazendo uso para isso do ![]() . O leitor terá assim um exemplo do que é tratado em nosso curso de Introdução ao
. O leitor terá assim um exemplo do que é tratado em nosso curso de Introdução ao com aplicações em Análise de Conjuntura. Nos capítulos anteriores, tratamos de duas das causas do aumento do endividamento [bruto] brasileiro nos últimos anos. O ocaso das operações compromissadas foi destrinchado no primeiro episódio da série, enquanto no segundo mostramos para o leitor como o Tesouro se endividou para capitalizar o BNDES. No capítulo de hoje, vamos nos ater a outra questão delicada no [ralo] debate sobre finanças públicas: a questão dos juros "pagos" para rolar a dívida pública. A culpa, afinal, é dos "rentistas"?
Quem não quer ficar molhado, que fique em casa durante a chuva...
O tema é espinhoso, leitor, eu sei. Como já deve ter percebido, o tema das finanças públicas é complexo, exige alguns pré-requisitos não apenas teóricas, mas igualmente práticos. É preciso saber lidar com dados que, de maneira geral, não estão facilmente disponíveis. Logo, é fácil se encantar por leituras equivocadas da situação. Uma delas, que toma conta do [ralo] debate sobre o assunto em alguns círculos intelectuais do país diz respeito ao seguinte enredo. A culpa pelo alto endividamento brasileiro é dos "rentistas", grupo que cooptou o Comitê de Política Monetária (Copom) do Banco Central e determina, em última instância, o nível da taxa de juros. Seria essa a explicação pela qual os juros no Brasil são extremamente elevados.
É complicado discutir/debater com pessoas que, em geral, não possuem o devido treinamento para lidar com um tema tão complicado. O custo de não discutir/debater, entretanto, é ver a política econômica sendo guiada por essas pessoas. Logo, leitor, penso que a melhor forma de termos um país melhor é tentar explicar que parte da culpa dos juros altos não é dos rentistas e sim de um governo que gasta sistematicamente mais do que arrecada ao longo do tempo. A irresponsabilidade fiscal parece ser uma das causa de pagarmos juros mais altos que países de mesmo nível de renda. Eu sei, essa parece ser uma explicação um tanto quanto anticlímax, dados os anseios distributivos da sociedade brasileira, expostos na Constituição de 88.
Mas falar não basta, não é mesmo? E eu sei que tudo que será mostrado a seguir converterá muito pouca gente. Pessoas que possuem o discurso dos "rentistas", em geral, não cedem a exercícios econométricos. E digo não por preconceito, mas por experiência própria. Correndo muitos riscos, desse modo, me ponho à chuva...
Vamos para o ![]() começar os trabalhos?
começar os trabalhos?
Em primeiro lugar, é preciso dizer que o governo brasileiro não tem condições de determinar preço e quantidade ao mesmo tempo. Em outras palavras, ele não consegue determinar a quantidade de dívida que emite e o preço dela, dado pela taxa de juros. Como vimos nos dois primeiros capítulos dessa série, o governo aumentou a dívida bruta em mais de 9 pontos percentuais do PIB, seja por causa das operações compromissadas, seja pelos repasses do Tesouro ao BNDES. Isto, somado a uma série de questões recorrentemente discutidas e analisadas nesse espaço, fez o preço da dívida disparar no período recente. Vimos isso no primeiro capítulo, ao colocar frente a frente o que chamamos de taxa de juros implícita e a taxa Selic. Hoje, vamos por outra ótica, baixando o arquivo zipado de necessidades de financiamento do setor público lá no site do Banco Central, deszipando e abrindo uma das planilhas do arquivo xls. Tudo, sem sair do ![]() , claro. O código para isso é posto abaixo.
, claro. O código para isso é posto abaixo.
library(XLConnect)
temp <- tempfile()
download.file("http://www.bcb.gov.br/ftp/notaecon/nfspp.zip",temp)
data <- unzip(temp, files='Nfspp.xls')
data <- loadWorkbook(data)
fluxo <- readWorksheet(data, sheet = "%-12meses(corrente)",
header = TRUE,
colTypes = 'numeric')
Feita a coleta de dados, o próximo passo é tratar o dado. Para o leitor ter uma ideia, a planilha que importamos para o ![]() tem a cara abaixo.
tem a cara abaixo.
Para tratar o dado, usamos o código abaixo.
######################################################################### ################### Tratar DADOS na Opção 01 ############################ ######################################################################### nfsp <- t(fluxo[-c(1:8),-c(1:2)]) nfsp <- ts(nfsp, start=c(2002,11), freq=12) colnames(nfsp) <- c(1:33) # Quantidade de séries. nfsp <- nfsp[,-c(11,22)] # Esse é o arquivo base.
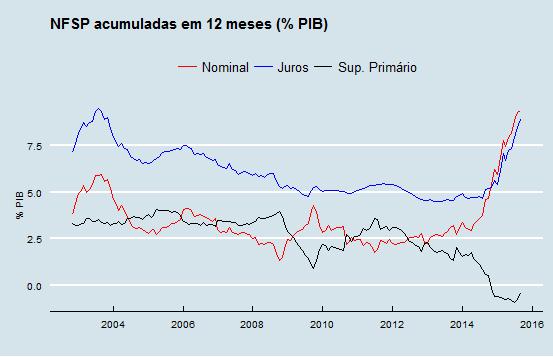
Das séries contidas no objeto nfsp, queremos analisar mais detidamente o déficit nominal, os juros nominais pagos e o superávit primário. Um gráfico com essas três séries é posto abaixo.
O leitor deve saber que o déficit nominal é igual aos juros pagos menos o superávit primário. Este, por sua vez, é a diferença entre receitas e despesas não financeiras. Logo, toda vez que o superávit primário cai, o déficit nominal aumenta. Ocorre o mesmo quando os juros pagos se elevam, gerando pressão sobre o déficit nominal. Essa é a realidade dos últimos meses, como ilustra o gráfico acima.
A nítida queda do Superávit Primário nos últimos anos
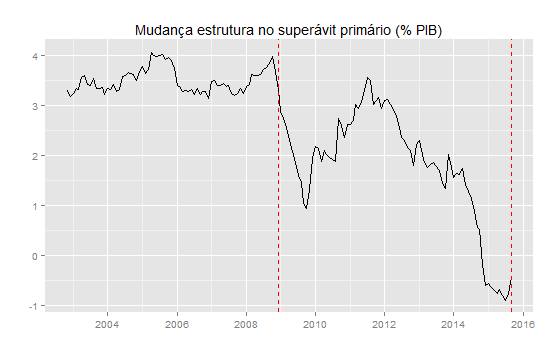
Nosso objetivo nesse breve post é verificar se o superávit primário ajuda a explicar os juros nominais pagos, ou o contrário ocorre. Nossa hipótese, derivada da teoria e dos dois posts anteriores dessa série, é de que um governo que gasta sistematicamente mais do que arrecada acaba se endividando mais, o que leva os compradores de títulos públicos a exigirem um preço mais elevado, refletido em gastos com juros maiores. Desse modo, a culpa não seria dos rentistas, mas do próprio governo, que não controla seus gastos de forma adequada. No gráfico acima, é possível ver uma queda do superávit primário. Vamos ampliar nossa compreensão dessa variável fazendo uso do pacote changepoint e da função cpt.meanvar, que verifica mudanças na média e na variância. O gráfico abaixo ilustra a nítida mudança no primário.
De fato, o que as linhas vermelhas tracejadas mostram é uma mudança no nível do primário depois de 2009. Até a eclosão da crise, o primário oscilava entre 3% e 4% do PIB. Depois de 2012, entretanto, há uma nítida tendência de queda, culminando em um déficit primário em 2014. O corolário disso é um aumento do risco de default do setor público brasileiro, refletido em aumento dos juros nominais pagos para rolar a dívida. Mas, claro, como podemos ver que é esse mesmo o caso, isto é, que o superávit primário ajuda a explicar os juros pagos?
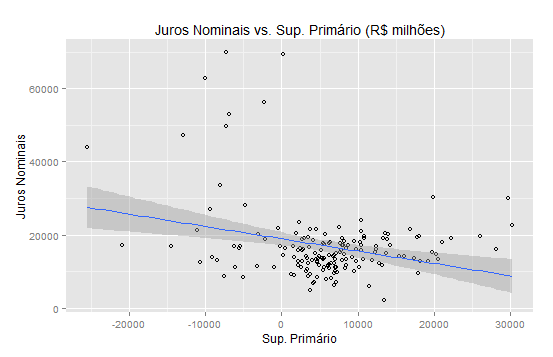
Superávit Primário vs. Juros Nominais
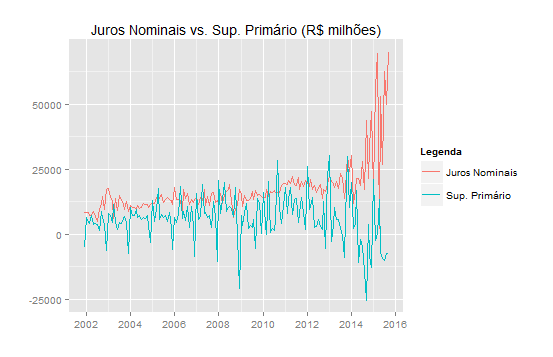
Um ponto que sempre chama atenção em debates sobre política fiscal é a ideia de que o governo paga juros muito altos para rolar a dívida pública. E isso, de acordo com alguns, seria culpa dos rentistas, que vivem desses juros. Para tentar melhorar a compreensão sobre esse tópico, vamos elaborar aqui um breve exercício, envolvendo um teste de causalidade de Granger. Para isso, vamos tomar as séries mensais dos juros pagos e do superávit primário. O gráfico abaixo ilustra o comportamento dessas séries.
E um gráfico da correlação entre elas.
Os testes de estacionariedade das séries são postos abaixo. Primeiro, um teste ADF.
| Time Trend: | Constant: | Neither: | |
| Juros.Nominais | 2.118 | 3.279 | 3.446 |
| Sup..Primário | -2.864 | -2.754 | -1.571 |
| 1 Pct | -3.990 | -3.460 | -2.580 |
| 2.5 Pct | -3.690 | -3.140 | -2.230 |
| 5 Pct | -3.430 | -2.880 | -1.950 |
| 10 Pct | -3.130 | -2.570 | -1.620 |
Depois, um teste KPSS.
| Time Trend: | No Trend: | |
| Juros.Nominais | 0.370 | 2.071 |
| Sup..Primário | 0.271 | 0.308 |
| 1 Pct | 0.216 | 0.739 |
| 2.5 Pct | 0.176 | 0.574 |
| 5 Pct | 0.146 | 0.463 |
| 10 Pct | 0.119 | 0.347 |
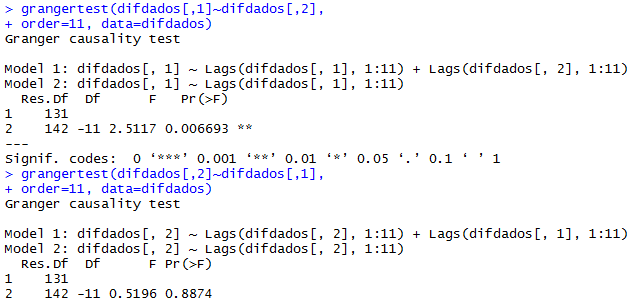
Os juros nominais não passam no teste, enquanto o primário passa. Desse modo, temos uma decisão a tomar. Diferenciar ambas as séries ou diferenciar apenas a série de juros nominais. Eu fiz ambos e rodei um teste de causalidade de Granger. O resultado final se modifica apenas em relação à defasagem, que foi escolhida com base no que apontou a maioria dos critérios de informação. Abaixo, coloco o resultado quando ambas as séries são diferenciadas.
O resultado de cima ilustra o teste para o superávit primário não granger causa os juros nominais, o que é rejeitado, conforme o p-valor. No resultado de baixo, está a hipótese contrária, que não pode ser rejeitada. Abaixo, avaliamos os mesmos testes para outras defasagens.
| Def | Juros | SP |
| 1 | 0.157 | 0.433 |
| 2 | 0.219 | 0.135 |
| 3 | 0.247 | 0.113 |
| 4 | 0.353 | 0.087 |
| 5 | 0.168 | 0.213 |
| 6 | 0.201 | 0.262 |
| 7 | 0.279 | 0.036 |
| 8 | 0.603 | 0.026 |
| 9 | 0.694 | 0.049 |
| 10 | 0.939 | 0.006 |
| 11 | 0.887 | 0.007 |
| 12 | 0.804 | 0.004 |
A tabela acima ilustra que quando a variável explicativa no teste é o juro nominal, não é possível rejeitar a hipótese nula em nenhuma defasagem. Com a variável explicativa sendo o superávit primário, entretanto, é possível rejeitar na quarta e a partir da sétima defasagem a hipótese nula. Ao diferenciar apenas os juros nominais, o resultado é posto abaixo.
| Def | Juros | SP |
| 1 | 0.217 | 0.336 |
| 2 | 0.411 | 0.195 |
| 3 | 0.538 | 0.0004 |
| 4 | 0.815 | 0.0002 |
| 5 | 0.759 | 0.00002 |
| 6 | 0.814 | 0.0001 |
| 7 | 0.839 | 0.00002 |
| 8 | 0.652 | 0.00005 |
| 9 | 0.858 | 0.00004 |
| 10 | 0.890 | 0.0001 |
| 11 | 0.839 | 0.0003 |
| 12 | 0.832 | 0.001 |
Como se fosse uma conclusão...
O que quisemos fazer aqui, leitor, foi mostrar que as evidências corroboram a teoria de que o que explica os juros elevados pagos pelo governo é, em parte, sua própria irresponsabilidade fiscal. O leitor pode se inspirar e tentar um exercício um tanto quanto mais robusto do que fizemos aqui. Fique à vontade! E, claro, na próxima vez que alguém lhe disser que a culpa é dos rentistas, desconfie do seu interlocutor... 🙂
________________________________________________________________________________
Gostou do post? Nós podemos lhe ensinar a fazer esse e outros exercícios em nosso curso de Introdução ao com aplicações em Análise de Conjuntura.
________________________________________________________________________________