[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]
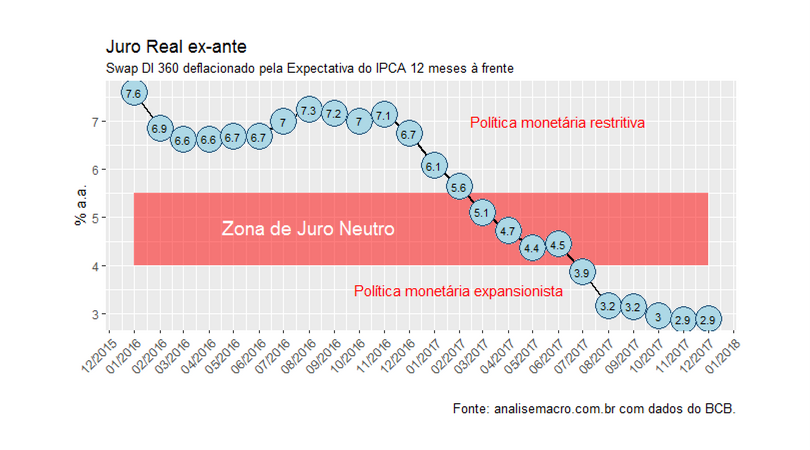
O Comitê de Política Monetária reduziu agora há pouco a taxa básica de juros em 50 pontos-base, levando-a para 7% a.a., o menor valor da série histórica. Isso deve se refletir, com efeito, no juro real ex-ante, que está próximo a 3% como ilustra o código e o gráfico abaixo.
library(ggplot2)
library(BETS)
library(xts)
library(scales)
library(mFilter)
swap = BETS.get(7806)
swap = swap[complete.cases(swap),]
swap$date = as.Date(swap$date, format='%d/%m/%Y')
swap = xts(swap$value, order.by = swap$date)
swap = apply.monthly(swap, FUN=mean)
swap = ts(swap, start=c(1999,8), freq=12)
expectativa = read.csv('expectativa.csv', header=T, sep=';', dec=',')
expectativa$date = as.Date(expectativa$date, format='%d/%m/%Y')
expectativa = xts(expectativa$expectativa, order.by = expectativa$date)
expectativa = apply.monthly(expectativa, FUN=mean)
expectativa = ts(expectativa, start=c(2001,11), freq=12)
data = ts.intersect(swap, expectativa)
juroreal = (((1+(data[,1]/100))/(1+(data[,2]/100)))-1)*100
jr = window(juroreal, start=c(2016,01))
df = data.frame(time=as.Date(time(jr)), juroreal=jr)
ggplot(df, aes(x=time, y=juroreal))+
annotate("rect", fill = "red", alpha = 0.5,
xmin = min(df$time),
xmax = max(df$time),
ymin = 4, ymax = 5.5)+
annotate('text', x=as.Date('2016-08-01'), y=4.8,
label='Zona de Juro Neutro',
colour='white', size=5)+
annotate('text', x=as.Date('2017-06-01'), y=7,
label='Política monetária restritiva',
colour='red', size=4)+
annotate('text', x=as.Date('2017-02-01'), y=3.5,
label='Política monetária expansionista',
colour='red', size=4)+
geom_line(size=.8)+
scale_x_date(breaks = date_breaks("1 months"),
labels = date_format("%m/%Y"))+
theme(axis.text.x=element_text(angle=45, hjust=1))+
geom_point(size=9, shape=21, colour="#1a476f", fill="lightblue")+
geom_text(aes(label=round(juroreal,1)), size=3,
hjust=0.5, vjust=0.5, shape=21, colour="black")+
xlab('')+ylab('% a.a.')+
labs(title='Juro Real ex-ante',
subtitle='Swap DI 360 deflacionado pela Expectativa do IPCA 12 meses à frente',
caption='Fonte: analisemacro.com.br com dados do BCB.')
Como ilustra o gráfico, a propósito, a poítica monetária se situa nesse momento em posição expansionista, contribuindo para a retomada do nível de atividade. Isso ocorre com expectativas de inflação 12 meses à frente próximas à 4%, abaixo, portanto, da meta de inflação.
[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2017/12/modelos.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/central-banking-training/modelos-do-banco-central/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]
[/et_pb_image][/et_pb_column][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2017/11/datascience.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]
[/et_pb_image][/et_pb_column][/et_pb_row][/et_pb_section]