Estacionariedade de Séries Temporais

Neste artigo, vamos apresentar o conceito de estacionariedade, verificar como estimar e interpretar aplicando em exemplos do mundo real usando as linguagens de programação R e Python. Além disso, apresentamos conceitos sobre série temporal e tipos de processos estocásticos.

Processo Estocástico e Séries Temporais

Um Processo Estocástico pode ser definido como uma coleção de variáveis aleatórias ordenadas no tempo, ${x_t, t \in T}$ , onde $T$ é um conjunto ordenado de índices.

Por exemplo, se temos a série do PIB trimestral, como definimos ela como um processo estocástico?

Basicamente, o valor do PIB em determinado trimestre pode ser qualquer um, a depender do clima econômico e político, portanto, se tivermos um valor $Y$ qualquer do PIB no período, temos uma realização particular de todas as possibilidades do processo, ou seja, se tivermos o histórico de 1950 até 2023 para o Brasil, temos as realizações particulares do processo, e portanto, uma amostra.

Do mesmo modo que utilizamos as amostras de dados para extrair inferências sobre a população, utilizamos, em séries temporais, a realização para extrair inferências sobre o processo estocástico subjacente.

Nestas condições, um processo estocástico é uma família de variáveis aleatórias, que supomos definidas em um mesmo espaço de probabilidades. Portanto, o processo estocástico desconhecido é o que chamamos de processo gerador dos dados que formam uma série temporal.

Componentes de uma série temporal

De modo a compreender o processo gerador de dados de uma determinada série temporal, pode ser interessante decompô-la em alguns componentes, como abaixo:

Componentes

Tendência

Uma tendência existe quando há um aumento ou diminuição de longo prazo nos dados. Não precisa ser linear. Às vezes, nos referiremos a uma tendência como “mudança de direção”, quando ela pode passar de uma tendência crescente para uma tendência decrescente.

Sazonalidade

Um padrão sazonal ocorre quando uma série temporal é afetada por fatores sazonais, como a época do ano ou o dia da semana. A sazonalidade é sempre de um período fixo e conhecido.

Ciclo e o Termo de erro

Um ciclo ocorre quando os dados exibem aumentos e quedas que não são de uma frequência fixa. Essas flutuações geralmente são devidas a condições econômicas e geralmente estão relacionadas ao “ciclo de negócios”. A duração dessas flutuações é geralmente de pelo menos 2 anos.

Quando decompomos uma série temporal em componentes, geralmente combinamos a tendência e o ciclo em um único componente de ciclo de tendência (geralmente chamado apenas de tendência para simplificar).

Assim, podemos pensar em uma série temporal como compreendendo três componentes: um componente de ciclo de tendência, um componente sazonal e um componente restante/termo de erro, em que este último representa qualquer outra coisa na série temporal, além dos outros componentes.

A figura acima contém diversas séries econômicas. Quais são os componentes de cada uma?

Pontos importantes:

Para algumas séries temporais (por exemplo, aquelas que são observadas pelo menos diariamente), pode haver mais de um componente sazonal, correspondendo aos diferentes períodos sazonais.

Decomposição

Temos uma representação dos componentes de acordo com as seguintes equações:

$y_{t} = S_{t} + T_{t} + R_t$

Onde, no tempo $t$ , $y_{t}$ é uma série temporal, $T_{t}$ é uma tendência, $S_{t}$ é um efeito sazonal e $R_t$ é um termo de erro.

Alternativamente, temos a decomposição multiplicativa:

$y_{t} = S_{t} \times T_{t} \times R_t$

A decomposição aditiva é a mais adequada se a magnitude das flutuações sazonais, ou a variação em torno do ciclo de tendência, não varia com o nível da série temporal.

Quando a variação no padrão sazonal, ou a variação em torno do ciclo de tendência, parece ser proporcional ao nível da série temporal, então uma decomposição multiplicativa é mais apropriada. Decomposições multiplicativas são comuns em séries temporais econômicas.

Tipos de processos

Um processo estocástico é caracterizado pela função de distribuição conjunta das variáveis aleatórias no tempo ( $y_1,y_2, \dotsc y_t$ ).

Dizemos que conhecemos a estrutura probabilística de um processo estocástico quando temos conhecimento dessas distribuições. No entanto, para obter esse conhecimento, normalmente precisamos observar um grande número de realizações, o que nem sempre está disponível quando se trata de séries econômicas.

Portanto, ao avaliar um processo, devemos ter em mente qual o comportamento de suas distribuição, e portanto, das funções da distribuição

1) Função da média: $\mu_t = E[y_t]$ ;

2) Função da Variância: $\sigma^2_t = Var[y_t]$ ;

3) Função da autocovariância/autocorrelação: $\gamma = E[(y\_{t}-\mu)(y\_{t-k}-\mu)] \quad \rho = \frac{\gamma}{\sigma^2}$ .

A partir do entendimento acima, separamos os processos em dois tipos:

Processos Estacionários

Um processo estocástico é considerado estacionário quando suas propriedades estatísticas não mudam com o tempo. Isso significa que a média, a variância e a covariância entre as variáveis aleatórias do processo permanecem constantes ao longo do tempo.

Em termos mais gerais, um processo estacionário exibe a mesma estrutura estatística em qualquer período de tempo considerado. Existem diferentes formas de estacionariedade, como estacionariedade no sentido amplo (wide-sense stationarity) e estacionariedade no sentido estrito (strict-sense stationarity).

Processos Não Estacionários

Um processo estocástico é considerado não estacionário se suas propriedades estatísticas variarem ao longo do tempo. Isso pode incluir tendências, flutuações sazonais ou mudanças estruturais.

Um processo não estacionário pode apresentar média e/ou variância que mudam ao longo do tempo, tornando suas propriedades estatísticas dependentes do tempo. Esses processos são mais complexos de modelar e prever, uma vez que suas características estatísticas estão em constante evolução.

Exemplos de Processos

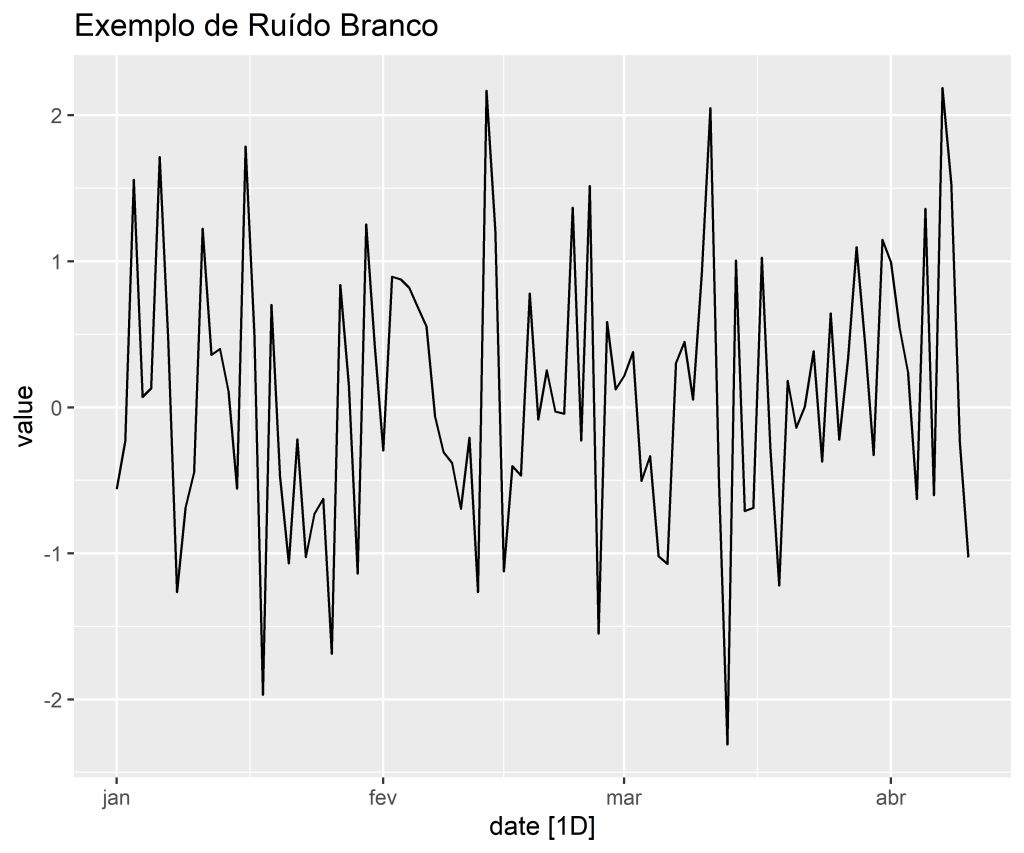
Ruído Branco

Imaginemos um modelo, em que os resíduos, isto é, a diferença entre os valores observados e aqueles preditos,

$\varepsilon_{t} = y_{t} - \hat{y}_{t}$

são ruídos brancos ser considerarmos que:

A média dos resíduos é zero, o que significa que eles se distribuem em torno de zero sem um viés positivo ou negativo;
A variância dos resíduos é constante, o que significa que a dispersão dos valores dos resíduos não muda ao longo do tempo;
Os resíduos em diferentes pontos no tempo são independentes entre si, o que significa que um valor de resíduo não está relacionado ao valor de resíduo em outro ponto no tempo.

Em outras palavras, uma série ${y_{t}: t = 1, 2, 3, ..., m}$ qualquer, e não apenas os resíduos, será considerada um ruído branco se $y_{1}, y_{2}, ..., y_{n}$ forem independentes e identicamente distribuídos com média igual a zero e variância constante.

Assumindo covariância igual a zero, temos, ademais, um ruído branco Gaussiano. Estamos assumindo, claro, uma distribuição normal.

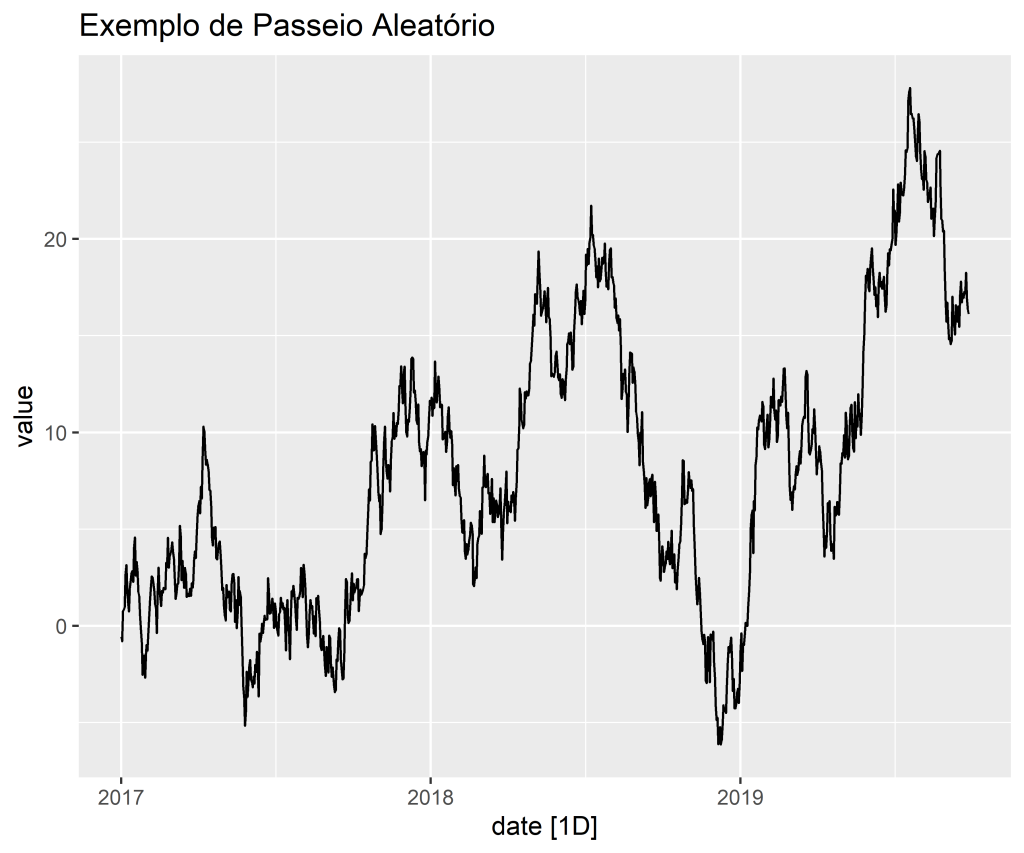
Passeio Aleatório (Random Walk)

Suponha que temos uma série temporal $y_{t}$ possa ser modelada como

$y_{t} = y_{t-1} + \varepsilon_{t}$

Onde $\varepsilon_{t}$ segue um ruído branco.

Substituindo $y_{t-1} = y_{t-2} + \varepsilon_{t-1}$ na equação acima e depois substituindo por $y_{t-2}$ , $y_{t-3}$ e assim por diante, temos:

(1) $\begin{equation*} y_{t} = \sum_{t=1}^{n} \varepsilon_{t} \end{equation*}$

Passeio Aleatório com drift

A do passeio aleatório pode ser modificada ao adicionarmos um intercepto, como abaixo:

(2) $\begin{equation*} y_{t} = \alpha + y_{t-1} + \varepsilon_{t} \end{equation*}$

Estacionariedade

O que é uma Série Temporal Estacionária?

Uma série temporal estacionária é aquela cujas propriedades estatísticas não dependem do momento em que a série é observada. Portanto, séries temporais com tendências ou sazonalidades não são estacionárias - a tendência e a sazonalidade afetarão o valor da série temporal em momentos diferentes.

Por outro lado, uma série de ruído branco é estacionária - não importa quando você a observe, ela deve parecer muito semelhante em qualquer ponto no tempo.

Alguns casos podem ser confusos - uma série temporal com comportamento cíclico (mas sem tendência ou sazonalidade) é estacionária. Isso ocorre porque os ciclos não têm um comprimento fixo, portanto, antes de observarmos a série, não podemos ter certeza de onde estarão os picos e vales dos ciclos.

Em geral, uma série temporal estacionária não terá padrões previsíveis a longo prazo. Os gráficos das séries mostrarão que a série é aproximadamente horizontal (embora algum comportamento cíclico seja possível), com variância constante.

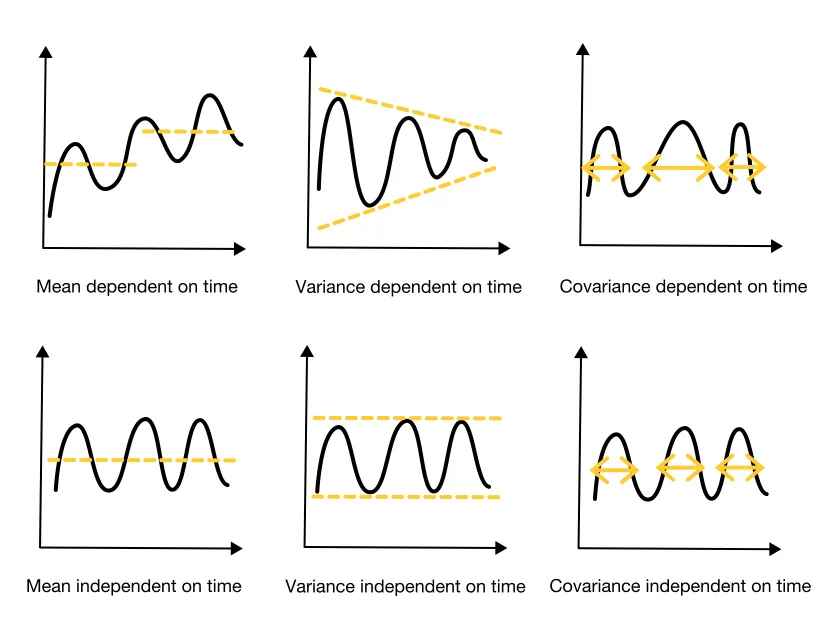
A estacionariedade descreve o conceito de que a forma como uma série temporal está se alterando permanecerá a mesma no futuro. Em termos matemáticos, uma série temporal é estacionária quando suas propriedades estatísticas são independentes do tempo:

Média constante;
Variância constante;
Covariância é independente do tempo.

Essa é a definição de estacionariedade no sentido amplo.

Outro tipo de estacionariedade é a estacionariedade estrita, que implica que amostras de tamanho idêntico têm distribuições idênticas. Como a estacionariedade estrita é restritiva e rara, concentraremos apenas na estacionariedade no sentido amplo.

Alguns modelos de previsão de séries temporais (por exemplo, modelos autorregressivos) requerem uma série temporal estacionária, pois são mais fáceis de modelar devido às suas propriedades estatísticas constantes. Portanto, é recomendado tornar a série temporal estacionária caso ela não seja

Como verificar a estacionariedade?

É possível testar uma série temporal quanto à estacionariedade de duas maneiras:

Abordagem intuitiva: Avaliação visual;
Abordagem estatística: Testes de raiz unitária.

Abordagem Intuitiva

Você pode avaliar visualmente a estacionariedade de uma série temporal dividindo mentalmente a série temporal ao meio e comparando a média, amplitude e comprimento do ciclo da primeira metade com a segunda metade da série temporal.

Média constante - O valor médio da primeira metade da série temporal deve ser semelhante ao da segunda metade;
Variância constante - A amplitude da primeira metade da série temporal deve ser semelhante à da segunda metade.
Covariância independente do tempo - O comprimento do ciclo na primeira metade da série temporal deve ser semelhante ao da segunda metade. Os ciclos devem ser independentes do tempo (por exemplo, não devem ser semanais ou mensais, etc.).

Abordagem estatística

Uma raiz unitária é uma tendência estocástica, isto é, um passeio aleatório com drift. Como o comportamento aleatório não pode ser previsto, isso significa:

Presença de raiz unitária: não estacionária (imprevisível);
Ausência de raiz unitária: estacionária

Para testar a estacionariedade, é necessário fazer o uso de um teste de raiz unitária, e portanto, é necessário criar hipóteses concorrentes:

Hipótese nula (H0) - por exemplo, a série temporal é estacionária (nenhuma raiz unitária presente);
Hipótese alternativa (H1) - por exemplo, a série temporal não é estacionária (raiz unitária presente)

Será avaliado se deve rejeitar ou não rejeitar a hipótese nula com base em duas abordagens:

Valor-p (p-value): Se o valor-p > 0,05, falha em rejeitar a hipótese nula. Se o valor-p ≤ 0,05, rejeita a hipótese nula;
Valor crítico: Se a estatística de teste for menor que o valor crítico, falha em rejeitar a hipótese nula. Se a estatística de teste for maior que o valor crítico, rejeita a hipótese nula. A abordagem do valor crítico deve ser usada quando o valor-p estiver próximo de ser significativo (por exemplo, em torno de 0,05).

Existem vários testes de raiz unitária que você pode usar para verificar a estacionariedade.

Observação: a depender do Teste, as regras acima se invertem.

Iremos nos concentrar nos mais populares:

Teste de Dickey-Fuller Aumentado (ADF);
Teste de Kwiatkowski-Phillips-Schmidt-Shin (KPPS).

Teste de Dickey-Fuller Aumentado

As hipóteses para o teste de Dickey-Fuller Aumentado (ADF) são:

Hipótese nula (H0): A série temporal não é estacionária porque há uma raiz unitária (se o valor-p > 0,05);
Hipótese alternativa (H1): A série temporal é estacionária porque não há raiz unitária (se o valor-p ≤ 0,05)

Teste de Kwiatkowski-Phillips-Schmidt-Shin

As hipóteses para o teste de Kwiatkowski-Phillips-Schmidt-Shin (KPSS) são:

Hipótese nula (H0): A série temporal é estacionária porque não há raiz unitária (se o valor-p > 0,05);
Hipótese alternativa (H1): A série temporal não é estacionária porque há uma raiz unitária (se o valor-p ≤ 0,05) Quanto mais positiva for essa estatística, maior a probabilidade de rejeitarmos a hipótese nula (temos uma série temporal não estacionária).

Exemplo prático:

Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.

Para fixar o conhecimento de forma aplicada usando ferramentas práticas de linguagem de programação, abaixo calculamos o coeficiente de autocorrelação das variáveis “taxa de juros Selic” e “taxa de inflação IPCA”, período 2005 a 2023. A fonte dos dados é o BCB e o IBGE.

No R, utilizamos o pacote aTSA.

No Python, veremos como construir através do uso de funções da biblioteca statsmodels.

R

Augmented Dickey-Fuller Test 
alternative: stationary 
 
Type 1: no drift no trend 
     lag    ADF p.value
[1,]   0 -1.071   0.296
[2,]   1 -0.718   0.422
[3,]   2 -1.019   0.314
Type 2: with drift no trend 
     lag   ADF p.value
[1,]   0 -2.55   0.113
[2,]   1 -1.52   0.514
[3,]   2 -1.79   0.409
Type 3: with drift and trend 
     lag    ADF p.value
[1,]   0 -2.393   0.410
[2,]   1 -0.635   0.975
[3,]   2 -0.568   0.978
---- 
Note: in fact, p.value = 0.01 means p.value <= 0.01

KPSS Unit Root Test 
alternative: nonstationary 
 
Type 1: no drift no trend 
 lag  stat p.value
   3 0.156     0.1
----- 
 Type 2: with drift no trend 
 lag  stat p.value
   3 0.156     0.1
----- 
 Type 1: with drift and trend 
 lag stat p.value
   3 0.11     0.1
----------- 
Note: p.value = 0.01 means p.value <= 0.01 
    : p.value = 0.10 means p.value >= 0.10

Código

Augmented Dickey-Fuller Test 
alternative: stationary 
 
Type 1: no drift no trend 
     lag   ADF p.value
[1,]   0 -4.09    0.01
[2,]   1 -3.35    0.01
[3,]   2 -2.90    0.01
Type 2: with drift no trend 
     lag   ADF p.value
[1,]   0 -7.47    0.01
[2,]   1 -6.52    0.01
[3,]   2 -5.95    0.01
Type 3: with drift and trend 
     lag   ADF p.value
[1,]   0 -7.51    0.01
[2,]   1 -6.56    0.01
[3,]   2 -6.00    0.01
---- 
Note: in fact, p.value = 0.01 means p.value <= 0.01

Código

KPSS Unit Root Test 
alternative: nonstationary 
 
Type 1: no drift no trend 
 lag stat p.value
   3 4.34    0.01
----- 
 Type 2: with drift no trend 
 lag  stat p.value
   3 0.108     0.1
----- 
 Type 1: with drift and trend 
 lag  stat p.value
   3 0.066     0.1
----------- 
Note: p.value = 0.01 means p.value <= 0.01 
    : p.value = 0.10 means p.value >= 0.10

Python

Teste ADF com drift e tendência do IPCA

Estatística de Teste:  -7.506329414731601

Valor Crítico:

1% :  -4.001305122770125
5% :  -3.431014101183445
10% :  -3.139106717487807

InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  warnings.warn(

Teste KPSS com drift e tendência do IPCA

Estatística de Teste:  0.08344328973633448

Valor Crítico:

10% :  0.119
5% :  0.146
2.5% :  0.176
1% :  0.216

Teste ADF com drift e tendência Selic

Estatística de Teste:  -1.669437432413694

Valor Crítico:

1% :  -4.001913294665537
5% :  -3.431306068757834
10% :  -3.1392777958611067

InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  warnings.warn(

Teste KPSS com drift e tendência Selic

Estatística de Teste:  0.10650286891083688

Valor Crítico:

10% :  0.119
5% :  0.146
2.5% :  0.176
1% :  0.2

Conclusão

Compreendemos neste artigo os conceitos de série temporal e processos estocástico. Vimos quais os tipos de componentes e os diferentes tipos de processos que uma série temporal segue, mostrando exemplos de alguns tipos. Por fim, entendemos o conceito de estacionariedade, sua aplicabilidade e como identificar uma série estacionária.

Saiba mais

Se você se interessa por análise e ciência de dados e quiser adquirir os conhecimentos e habilidades destacados neste artigo, dê uma olhadinha nessa formação especial que a Análise Macro preparou:

Especialista em Econometria e Machine Learning

E para obter os códigos completos deste exercício e de vários outros, dê uma olhada no Clube AM da Análise Macro, onde publicamos exercícios de ciência de dados toda semana em R e Python.

Referências

Forecasting: Principles and Practice Hyndman, R. & Athanasopoulos, G., 2021, 3rd ed. OTexts.

Box, G. E. P., G. M. Jenkins, G. C. Reinsel, e G. M. Ljung. 2016. Time Series Analysis. Editora Wiley.

Pfaff, B. 2008a. Analysis of Integrated and Cointegrated Time Series with R. Springer.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Transfer Learning: mostrando porque o Python está na ponta do desenvolvimento

Criando Tabelas com o Python: mostrando o poder da linguagem sobre o Excel

Análise do Censo Demográfico com o R

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Criando um Dashboard de análise de Ações no Python

Outros artigos relacionados

Transfer Learning: mostrando porque o Python está na ponta do desenvolvimento

A aprendizagem por transferência (transfer learning) é o reuso de um modelo pré-treinado em um novo problema. Portanto, sua utilização torna-se um avanço enorme para a previsão de diferentes tipos de variáveis, principalmente para aquelas ordenadas no tempo. Mostramos nesta postagem o uso do Transfer Learning com o Python para o caso de Séries Temporais.

Criando Tabelas com o Python: mostrando o poder da linguagem sobre o Excel

Nos dias atuais, pessoas que trabalham com dados estão constantemente confrontados com um dilema: criar uma tabela não tão genial no Excel ou manter em um formato ainda pior, como um dataframe, mas mantendo a flexibilidade de obtenção dos dados. Podemos resolver esse grande problema, unindo a flexibilidade e beleza ao usar a biblioteca great_tables do Python.

Análise do Censo Demográfico com o R

Como podemos analisar dados do Censo Demográfico para produzir pesquisas e implementar políticas públicas? Mostramos nesta postagem o resultado de uma breve análise dos dados preliminares do Censo Demográfico de 2022 usando o R.