O que é o Hiato do Produto?
A macroeconomia resulta da soma de milhões de decisões individuais descentralizadas. Todos os dias, agentes econômicos escolhem o que produzir, como produzir e como distribuir os recursos produtivos. O principal indicador desse esforço agregado é o Produto Interno Bruto (PIB), que representa a soma de todos os bens e serviços finais produzidos por um país dentro de um determinado período.
Decomposição do PIB: Produto Potencial e Hiato do Produto
Para entender melhor o conceito de hiato do produto, podemos decompor o PIB efetivo da seguinte forma:
Onde:
representa o PIB efetivo em um dado período t;
é o produto potencial, ou seja, a tendência de longo prazo do PIB;
é o hiato do produto, que mede o grau de ociosidade da economia.
O Produto Potencial reflete as condições estruturais da economia, como:
- População em idade ativa;
- Estoque de capital;
- Qualidade da educação;
- Instituições econômicas e políticas.
Já o Hiato do Produto reflete questões conjunturais, como:
- Política econômica (monetária e fiscal);
- Condições climáticas;
- Choques externos;
- Incertezas políticas.
No curto prazo, o PIB efetivo pode crescer acima ou abaixo do produto potencial, devido a flutuações cíclicas. No longo prazo, no entanto, o crescimento da economia é limitado pela disponibilidade de fatores de produção e pela forma como esses fatores são combinados.
O PIB e a Função de Produção Cobb-Douglas
Uma forma comum de modelar a estrutura produtiva de uma economia é através da Função de Produção Cobb-Douglas, com retornos constantes de escala:
Onde:
é o estoque de capital;
é a força de trabalho;
representa a produtividade total dos fatores (PTF);
mede a participação do capital na renda nacional.
O produto potencial representa o nível máximo de PIB que pode ser sustentado sem pressões inflacionárias significativas. No curto prazo, a diferença entre o PIB efetivo
e o produto potencial
é o hiato do produto
.
Como Estimar o Hiato do Produto?
Calcular o hiato do produto não é trivial, pois o produto potencial não é uma variável diretamente observável. Para estimá-lo, utilizamos diferentes métodos:
- Filtros Univariados (suavização do PIB ao longo do tempo);
- Filtros Multivariados (incorporando mais variáveis econômicas);
- Função de Produção (baseada na Cobb-Douglas).
Nenhum método é perfeito, mas cada um traz informações valiosas sobre o comportamento da economia. Por isso, recomenda-se a comparação de diferentes métodos para entender melhor as incertezas associadas a essa variável não observável.
Métodos de Estimação do Hiato do Produto no Python
No nosso estudo, implementamos os seguintes métodos de estimação do hiato do produto em Python:
- Tendência Linear (MQO)
- Tendência Quadrática (MQO)
- Filtro Hodrick-Prescott (HP)
- Filtro de Hamilton
- Hiato estimado pela Instituição Fiscal Independente (IFI) (importação)
- Hiato estimado pelo Banco Central do Brasil (BCB) (importação)
Para os hiatos estimados por filtro foi utilizado a biblioteca statsmodels. Já os Hiato estimados pela IFI e pelo BCB foram importados de seus respectivos sites, enquanto os demais foram estimados via Python.
Resultados e Análises do Hiato do Produto no Python
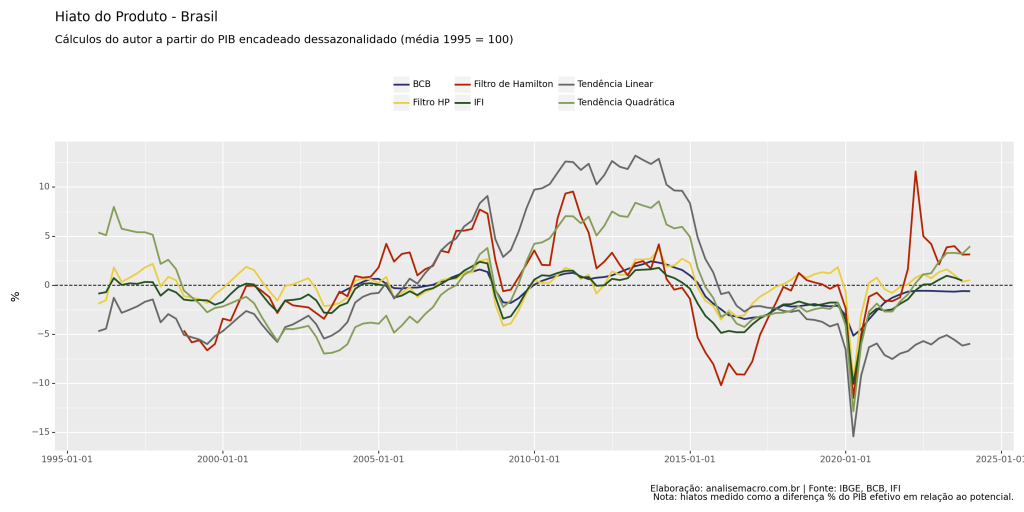
O gráfico abaixo apresenta a trajetória das diferentes medidas do hiato do produto até 2024Q1. Os principais destaques são:
- Apenas o Hiato do BCB e o Tendência Linear apresentam valores negativos na margem;
- As demais medidas estão acima de 0%, sugerindo que a economia não está ociosa;
- Comparações entre os métodos ajudam a entender cenários econômicos distintos e possíveis impactos na política econômica.
 Um ponto relevante que deve ser levado em considerações é o problema de fim de amostra do Hiato estimado via Filtros Estatísticas. Falamos sobre essa questão na seguinte postagem: Investigando o problema de fim de amostra na estimativa do Hiato do Produto usando a linguagem R.
Um ponto relevante que deve ser levado em considerações é o problema de fim de amostra do Hiato estimado via Filtros Estatísticas. Falamos sobre essa questão na seguinte postagem: Investigando o problema de fim de amostra na estimativa do Hiato do Produto usando a linguagem R.
Estatística Descritivas dos Hiatos
Um ponto a se observar é do que as medidas de Hiato estimadas via Função de Produção (IFI e BCB) são menos voláteis, e possuem médias negativas, comparando-se às medidas de Tendências.
Código
| Tendência Linear | Tendência Quadrática | Filtro HP | Filtro de Hamilton | IFI | BCB | |
|---|---|---|---|---|---|---|
| count | 113.000000 | 113.000000 | 113.000000 | 102.000000 | 112.000000 | 82.000000 |
| mean | 0.205512 | 0.096821 | 0.016547 | 0.094519 | -0.967768 | -0.536463 |
| std | 6.528785 | 4.431386 | 1.808351 | 4.352085 | 1.905623 | 1.711461 |
| min | -15.410280 | -12.843644 | -9.825693 | -11.501185 | -10.060000 | -5.150000 |
| 25% | -4.623414 | -3.105382 | -0.850595 | -2.121579 | -1.942500 | -1.907500 |
| 50% | -2.297429 | -1.284489 | 0.399859 | 0.183379 | -0.795000 | -0.455000 |
| 75% | 4.772593 | 4.218755 | 1.127790 | 2.543618 | 0.365000 | 0.812500 |
| max | 13.202287 | 8.545595 | 3.727109 | 11.594277 | 2.380000 | 2.430000 |
_____________________________________
Quer aprender mais?
Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.


