O Índice Bovespa ou simplesmente conhecido como Ibovespa, é o indicador mais importante no acompanhamento da cotação das ações negociadas na B3, a bolsa de valores brasileira. O índice, por suposto, acompanha a variação de preços das ações das maiores empresas do Brasil, isto é, a depender dos resultados operacionais e financeiros das companhias, os seus preços acompanharão as expectativas dos investidores com base nesses resultados, ou seja, a Ibovespa acompanhará essa mesma trajetória.
Dito isto, a depender dos resultados das empresas, o crescimento do país é afetado, e um bom indicador para saber a trajetória da economia real do país é a Formação Bruta de Capital Físico. Nesse post, investigaremos se existe uma relação do Ibovespa com a FBCP por meio da estimação de um Vetor de Correção de Erros (VEC) e de uma análise das funções impulso-resposta.
Primeiro devemos coletar os dados necessários. Abaixo realizamos a coleta e o tratamento de dados do Ibovespa, além de trimestralizar a série.
library(quantmod) library(xts) library(sidrar) library(timetk) library(tidyverse)
# IBOVESPA
## Coleta os dados do Yahoo Finance
getSymbols("^BVSP", src= "yahoo",
from= as.Date('2001-01-01'))
## Captura os preços de fechamento
ibovespa <- Cl(BVSP) %>%
na.omit() %>%
`colnames<-`("ibovespa")
## Transforma em trimestral
ibov_qtr <- apply.quarterly(ibovespa, FUN = mean) %>%
tk_tbl(preserve_index = TRUE,
rename_index = "date") %>%
mutate(date = as.yearqtr(date, type = "%Y%q"))
## Cria o objeto ts
ibov_qtr_ts <- ts(ibov_qtr$ibovespa, start=c(2001,01), freq = 4)
Em seguida, fazemos o mesmo para a FBCF.
# FBCF ## Coleta os dados do SIDRA e calcula o crescimento interanual fbcf = get_sidra(api="/t/1620/n1/all/v/all/p/all/c11255/93406/d/v583%202") %>% dplyr::select(date = "Trimestre (Código)", value = "Valor") %>% mutate(date = as.yearqtr(date, format = "%Y%q"), dfbcf = (value/lag(value, 4) -1) * 100) ## Cria o objeto ts fbcf_ts = ts(fbcf$value, start=c(1996,01), freq=4) dfbcf_ts = (fbcf_ts/stats::lag(fbcf_ts, -4) -1) * 100
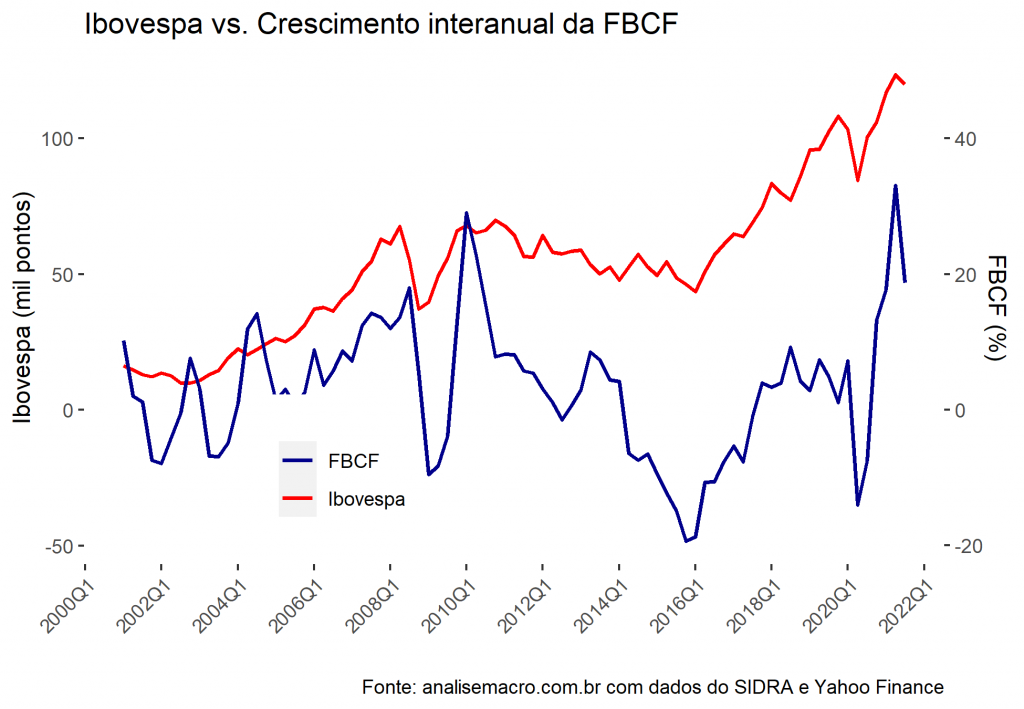
Em seguida, podemos visualizar as séries em conjunto para investigar a relação de ambos ao longo do tempo.
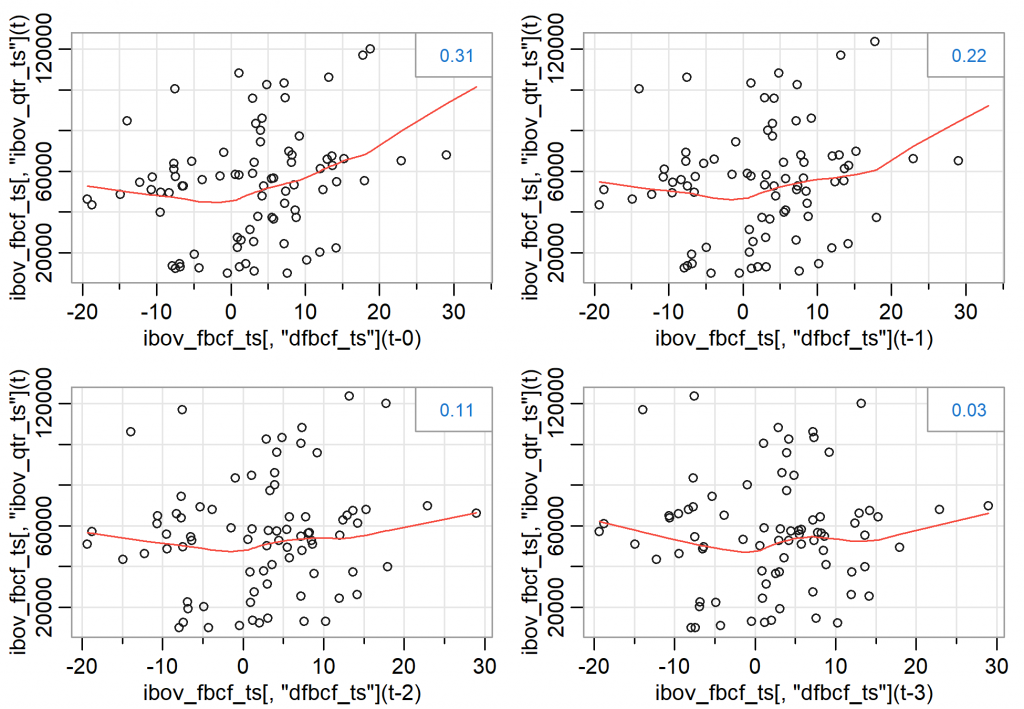
De outra forma, é possível visualizar a correlação entre as séries em suas defasagens, vemos que quanto maior a defasagem, menor a correlação.
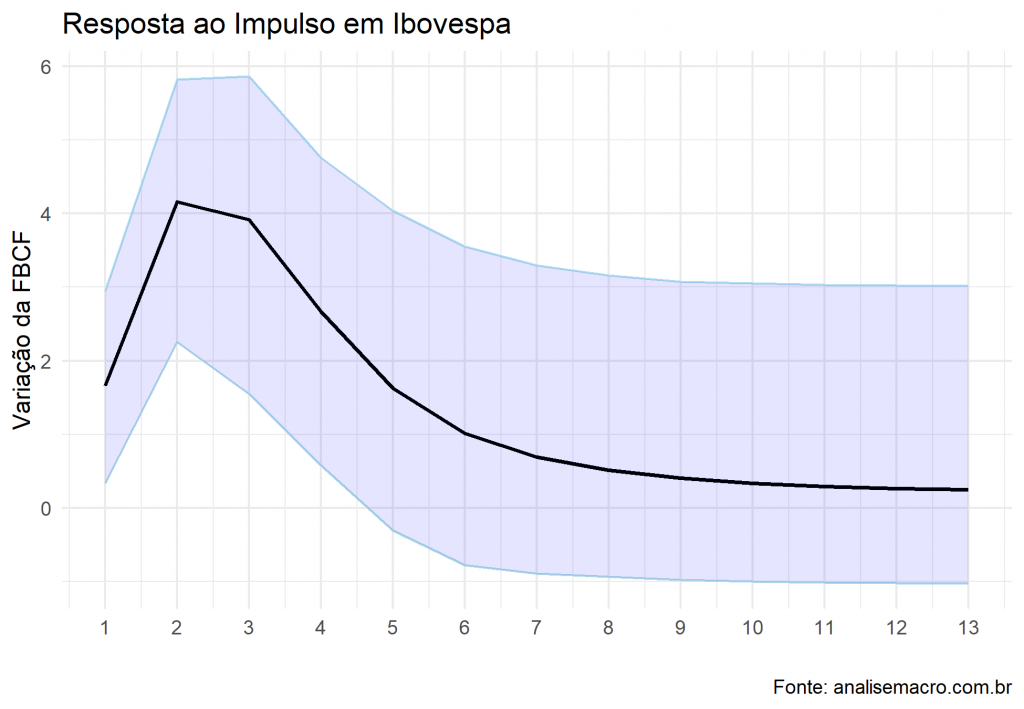
Por fim, construímos um modelo de Vetor de Correção de Erros (VEC) entre as duas séries, de forma que seja possível investigar as funções impulso-resposta. Vemos que a partir da metodologia, um choque na Ibovespa tem efeito sobre a variação da FBCF. Vemos isto no gráfico abaixo.
Por meio da metodologia utilizada no post foi possível averiguar a existência de relação entre os dois indicadores. Para que você consiga descobrir fenômenos como esse, os nosso cursos de Macroeconomia, Séries Temporais e Finanças Quantitativas são fundamentais para esse aprendizado, auxiliando tanto na teoria quanto na prática.
