No nosso Curso de Microeconometria usando o R, nosso objetivo é capacitar alunos de graduação e pós-graduação, professores e profissionais de mercado em econometria aplicada a microdados. O curso envolve tanto a apresentação teórica de modelos de regressão, quanto a aplicação no R de diversos exemplos associados a dados de corte transversal, séries de tempo e dados em painel. Espera-se que ao final do Curso o aluno tenha facilidade em desenvolver trabalhos empíricos empregando microdados.
Para ilustrar, vamos considerar hoje uma das aulas do Curso, envolvendo Regressões Quantílicas.
Regressões que utilizam o método de mínimos quadrados modelam a média condicional de uma variável de interesse. Isto é, , o valor esperado de
dado um vetor
. Às vezes, entretanto, podemos estar interessados em outras características da distribuição condicional, como por exemplo a mediana ou, de forma mais geral, os quantis.
O modelo de regressão quantílica pela função quantílica condicional
(1)
i.e., denota o quantil
de
condicionado a
. As estimativas são então obtidas minimizando
com respeito a
, onde para
,
denota a função linear por partes
, sendo
a função indicativa.
De modo a ilustrar a aplicação da regressão quantílica no R, vamos estimar o seguinte modelo:
(2)
Para estimar 2, nós recorremos à função `rq` do pacote `quantreg` e ao dataset **CPS1988**, como abaixo. Por default, `rq` seta , isto é, a mediana de
.
library(quantreg)
library(AER)
data('CPS1988')
cps_f <- log(wage) ~ experience + I(experience^2) + education
cps_lad <- rq(cps_f, data = CPS1988)
A seguir, o output da regressão.
| Dependent variable: | |
| log(wage) | |
| experience | 0.077*** |
| (0.001) | |
| I(experience2) | -0.001*** |
| (0.00003) | |
| education | 0.094*** |
| (0.001) | |
| Constant | 4.241*** |
| (0.022) | |
| Observations | 28,155 |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
A regressão quantílica é particularmente interessante quanto modelamos vários quantis de forma simultânea, como abaixo. Para isso, basta setar o argumento tau da função.
cps_rq <- rq(cps_f, tau = c(0.25, 0.75), data = CPS1988)
Uma questão natural derivada desse tipo de análise é se as linhas ou superfícies de regressão são paralelas; ou seja, se os efeitos dos regressores são uniformes nos quantis. Existe o método `anova()` para explorar esta questão.
cps_rq25 <- rq(cps_f, tau = 0.25, data = CPS1988) cps_rq75 <- rq(cps_f, tau = 0.75, data = CPS1988) anova(cps_rq25, cps_rq75, joint = FALSE)
Observamos que o efeito não é uniforme ao longo dos quantis, com as diferenças estando associadas ao coeficiente da **experiência**. Podemos ver essa diferença de modo gráfico com o código a seguir.
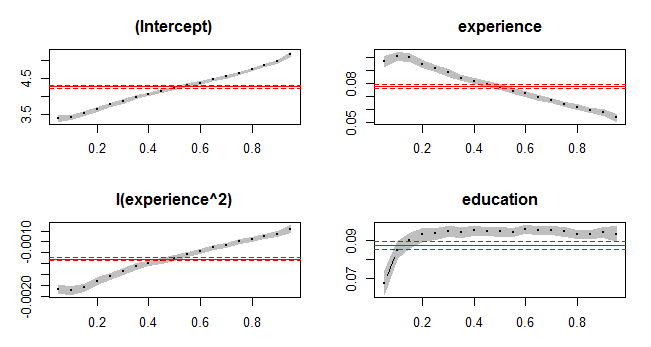
cps_rqbig <- rq(cps_f, tau = seq(0.05, 0.95, by = 0.05), data = CPS1988) cps_rqbigs <- summary(cps_rqbig) plot(cps_rqbigs)
Com isso, visualizamos a variação dos coeficientes em função de , sendo bastante claro que a influência das covariáveis está longe de ser uniforme. As áreas sombreadas representam intervalos de confiança pontuais de 90% (por padrão) para as estimativas da regressão quantílica. Para comparação, as linhas horizontais sólidas e tracejadas mostradas em cada gráfico representam a estimativa do OLS e um intervalo de confiança de 90% associado.
_________
(*) Cadastre-se aqui na nossa Lista VIP para receber um super desconto na abertura das Turmas 2021.