Modelos que usam o Google Trends vs. modelos que usam outras variáveis exógenas: como comparar?

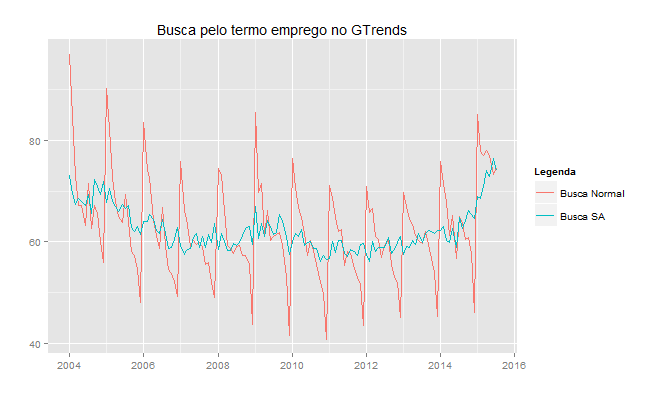
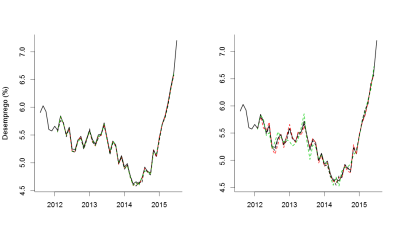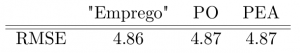O pessoal do NEOC e o Vítor tocaram, recentemente, no assunto sobre a possibilidade de usar informação do Google Trends na previsão de variáveis macroeconômicas. Em particular, a taxa de desemprego. Neste post, o pessoal do NEOC chegou à conclusão de que sim, existe uma melhora na previsão quando se utiliza o número de buscas (no Brasil) pelo termo "emprego". Aqui, procuramos aprofundar um pouco o assunto, tentando levar em consideração um detalhe importante. A grande vantagem de se utilizar estas variáveis do Google Trends é que elas estão contínuamente disponíveis. Isso implica no fato de que para comparar modelos que usam o gtrends com modelos que utilizam outras variáveis exógenas, é preciso torná-los "comparáveis".  Vejamos por quê.

Como as variáveis do gtrends estão continuamente disponíveis, não precisamos esperar o final do mês ou trimestre para "rodarmos" mais um modelo. Isto é, podemos estimar modelos como

   

onde a variável já é conhecida no instante . Isso implica que é preciso levar em consideração a defasagem entre o gtrends e outras variáveis exógenas que você possa colocar para tentar prever . Para comparar um modelo que usa o gtrends com modelos que utilizam outras variáveis exógenas, é preciso tornar esses modelos "comparáveis".  É basicamente isso que fazemos nesse exercício.

Nesse contexto, geramos dois conjuntos de previsões. Um primeiro conjunto assume que todas as variáveis são conhecidas no instante , isto é, tanto a população ocupada, a população economicamente ativa e o gtrends estão disponíveis em , quando queremos prever . No segundo conjunto, por outro lado, assumimos que as variáveis população ocupada e população economicamente ativa estão disponíveis em e o gtrends está disponível em , para prever . Ao invés de palavras, equações:

Conjunto 1

   

   

   

Conjunto 2

   

   

   

Onde é a quantidade de vezes que a palavra "emprego" foi utilizada como termo de busca no Brasil no mês .  Dada a diferença entre a disponibilidade de dados do gtrends e das demais variáveis exógenas, é preciso fazer alguns ajustes. Para isso devemos não só escolher uma medida, que neste caso foi o RMSE, de comparação entre modelos, mas também ter certeza de que a construção dessas medidas leva em consideração as diferenças entre os modelos estimados. Ou seja, devemos saber se estas medidas são efetivamente comparáveis (mais sobre as diferentes medidas você encontra aqui). Portanto, a construção deste exercício se deu da seguinte maneira:

i) Normalizar a amostra de forma que as estimações do conjunto 1 e do conjunto 2 utilizam o mesmo número de observações. Assim, modelos que somente usam variáveis defasadas usam o mesmo número de observações que modelos que usam variáveis em e . No isto pode ser feito de maneira bem simples utilizando a função embed.

ii) Dividir a amostra em duas partes, uma para estimação e outra para avaliação de previsão, isto é, uma parte para construção da medida escolhida. Assim tentamos garantir um número mínimo de observações para construir a estatística.

As figuras a seguir ilustram os resultados das previsões para o primeiro e para o segundo conjunto de previsões, respectivamente.

Como era de se esperar, se usarmos as informações da população ocupada e da população economicamente ativa em as previsões são melhores e, consequentemente, mais centradas nos valores observados. Caso contrário, se considerarmos a defasagem existente entre o gtrends e as demais variáveis exógenas, as previsões ficam mais "espalhadas". Note que, por causa disso, se assumirmos o modelo errado estaríamos construindo medidas erradas de avaliação. Dito isto, podemos construir as nossas medidas com base no segundo conjunto de previsões [aquele que considera a diferença entre o gtrends e as demais variáveis exógenas] e finalmente comparar o poder de previsão das diferentes variáveis.

Como podemos ver, a variável do Google Trends, mesmo nos dando informação, de certa maneira, "privilegiada", não nos ajuda tanto assim individualmente (pelo menos quando a medida escolhida de acurácia é o RMSE).

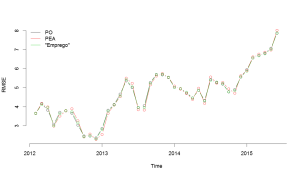
Finalmente, é interessante notar que os modelos utilizados neste post vêm se mostrando cada vez piores na hora de fazer previsões, como pode ser visto no gráfico a seguir. Estaria isso indicando alguma possível mudança na dinâmica do mercado de trabalho?

_______________________________________

Gostou do post? Quer aprender a fazer o mesmo? Dê uma olhada no nosso curso de Introdução ao R com aplicações em Análise de Conjuntura. Faça no Rio de Janeiro ou leve para sua empresa ou universidade!

________________________________________