Avaliando previsões com o R

Desde os tempos do GECE/UFF, quando tentávamos fazer previsões para o IPCA, eu sempre tive a mania de comparar modelos mais “complexos” ou que continham mais informação com outros mais simples. Na época, as comparações eram basicamente entre modelos ARIMA, ADL e VAR. Com o post recente do Vitor sobre a futura evolução do PIB, deu uma vontade de deixar de lado um pouco os estudos para a dissertação e estimar uns modelos.

Aproveitando minha recente re-descoberta do pacote BMR (para o R) e minha leitura das notas de aula de Gary Koop (feitas para o Banco Central coreano), resolvi reproduzir um dos modelos presentes em Koop e Korobilis (2010)* e comparar suas previsões para o PIB americano com as previsões de um modelo VAR e um ARIMA. Portanto, estendi o modelo deles para incluir não só taxa de juros, desemprego e inflação, mas também o PIB (sua taxa de variação frente ao trimestre do ano anterior, mais precisamente).

Os dados, expostos no gráfico abaixo, são todos trimestrais e retirados do site do FRED e a amostra total engloba dados desde o terceiro trimestre de 1954 até o quarto trimestre de 2014.

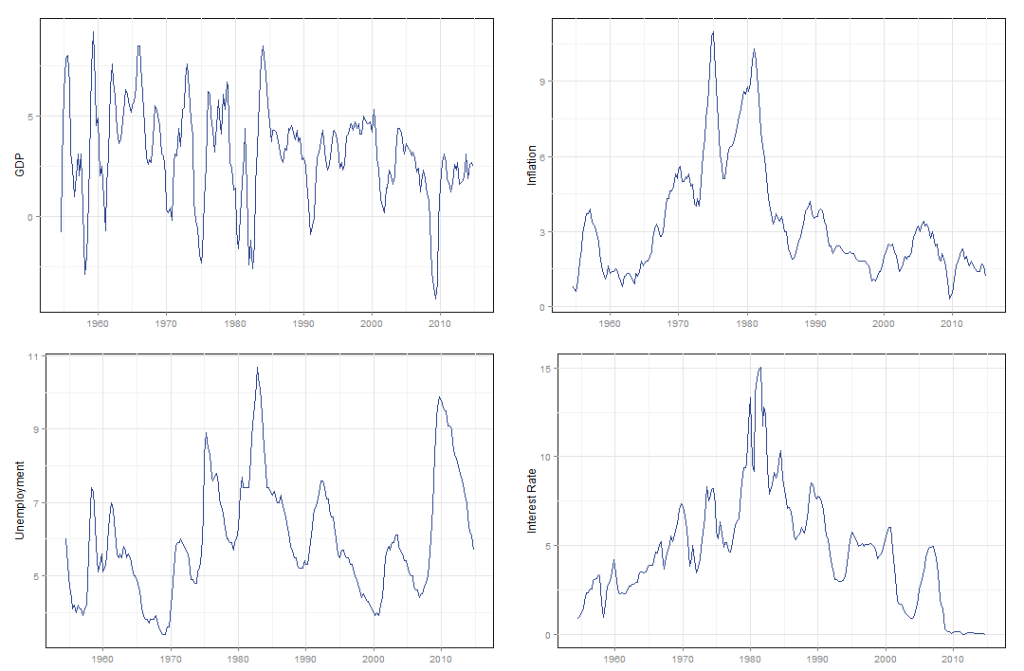
Decidi comparar a previsão dos modelos para dois períodos distintos, um mais curto começando a partir do primeiro trimestre de 2011 e outro mais longo, começando no primeiro trimestre de 2005. Assim, podemos tentar avaliar o poder de previsão dos diferentes modelos para diferentes prazos. Aqui surge o primeiro problema; como devemos comparar a previsão entre estes modelos ?

Bom, primeiro devemos definir o que é o erro de previsão. Para isso, assuma que estimamos um modelo que descreva a variável . Dado este modelo temos que a variável de interesse possa ser descrita como o valor previsto pelo modelo mais um erro não previsto pelo modelo, isto é

Logo, o erro de previsão é dado por

Em seguida, podemos definir o erro percentual, , como

Utilizando a função accuracy do pacote forecast, 7 medidas diferentes para a avaliação de previsão são calculadas. A seguir tentarei, de maneira breve, dar a ideia principal por trás de cada uma, seguindo basicamente o artigo de Hyndman e Koehler (2006)**. Neste artigo os autores separam as diferentes medidas em 4 categorias; medidas que dependem da escala, medidas baseadas em erros percentuais, medidas baseadas em erros relativos e medidas relativas. Aqui iremos tratar rapidamente das duas primeiras categorias e a última.

As três primeiras medidas fornecidas pertencem ao primeiro grupo e são: ME (Mean Error), RMSE (Root Mean Square) e MAE (Mean Absolute Error). A primeira consiste simplesmente na média da série de erros de previsão enquanto que a segunda é a raiz quadrada da média dos erros quadráticos. Finalmente, a terceira medida é dada pela média dos erros em valores absolutos.

Como mencionei anteriormente, estas três medidas fazem parte do grupo de medidas que dependem da escala na qual os dados estão. Logo, estas medidas podem ser utilizadas para efeito de comparação de diferentes modelos aplicados a mesma amostra de dados. Hyndman e Koehler (2006) chamam a atenção para o fato de que, apesar da medida RMSE ser mais utilizada, ela é mais sensível a outliers quando comparada com a MAE. Abaixo a fórmula para as três medidas.

A quarta e quinta medida fornecida, MPE (Mean Percentage Error) e MAPE (Mean Absolute Percentage Error), pertercem ao grupo de medidas que se baseiam no erro percentual de previsão. Neste caso MPE representa o erro percentual médio enquanto que MAPE é dada pela média do erro percentual em valor absoluto. Consequentemente estas medidas têm a vantagem de não serem dependentes de escala e podem assim serem utilizadas para comparar o poder de previsão utilizando dados com diferentes escalas.

Um problema óbvio destas medidas baseadas em erros percentuais é que elas não serão definidas para , além disso Hyndman e Kohler (2006) apontam para problemas que involvem a distribuição dos erros percentuais (quando ).

A sexta medida fornecida, ACF1, é o coeficiente de autocorrelação parcial de primeira ordem. Este coeficiente pode nos fornecer informação sobre a possível existência de estrutura nos erros de previsão. A ideia aqui é basicamente a seguinte: se o nosso modelo foi bem especificado o erro de previsão fornecido por ele deve ser completamente aleatório, logo não deve possuir nenhuma estrutura. Portanto, quando maior esta medida, maior será o indicio de existência de estrutura.

Finalmente, temos Theil's U, ou seja, o U de Theil. Esta medida pertence a categoria de medidas relativas e, neste caso específico, trata-se da razão entre a raiz quadrada da média do erro percentual quadrático e a raiz quadrada da média da taxa de variação percentual quadrática da série observada. Desta forma, o U de Theil nada mais é do que a comparação entre o modelo em questão e um simples passeio aleatório. Portanto, quanto menor o índice, melhor será o modelo (comparado com um passeio aleatório). Além disso, como se trata de valores ao quadrado, pesos maiores são atribuídos a erros mais discrepantes.

Relembrando que um passeio aleatório é dado por um processo AR(1), como abaixo

onde . Logo, o erro de previsão deste processo é dado por

Consequentemente, o erro percentual de previsão do passeio aleatório é

que é exatamente o termo no denominador do índice de Theil.

Assim, podemos concluir que, dada a saída da função accuracy, buscamos o modelo que apresente os menores valores para todas estas medidas. Feitas estas observações podemos prosseguir para o processo de estimação dos diferentes modelos.

De modo a economizar (bastante) tempo, para o modelo (S)ARIMA foi utilizado a função auto.arima (do pacote forecast de autoria do Rob Hyndman, que basicamente procura o melhor modelo de acordo com um critério de informação a gosto). Já o modelo VAR, para efeitos de comparação, foi estimado com o mesmo número de defasagens que o BVAR (com informação a priori de Minnesota) sugerido em Koop e Korobilis (2010).

O BVAR foi estimado com a função BVARM do pacote BMR, que dada algumas opções, é o mesmo modelo dado em Koop e Korobilis (2010). A média a priori dos coeficientes AR(1), 0.9 para todas as variáveis, das variáveis dependentes foram estabelecidas com base nos correlogramas das séries (figura abaixo).

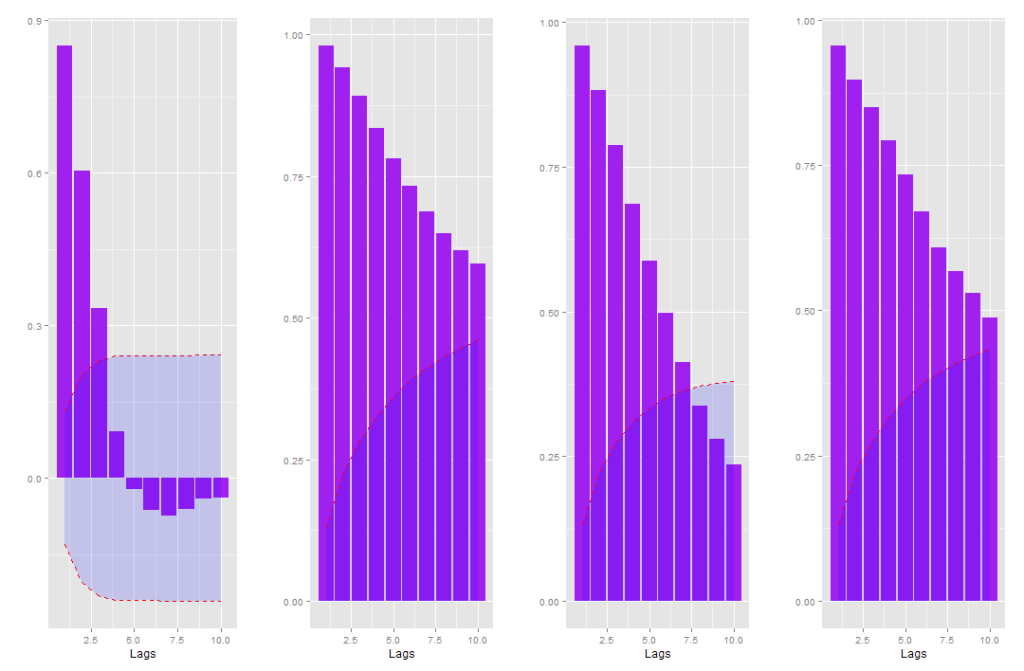
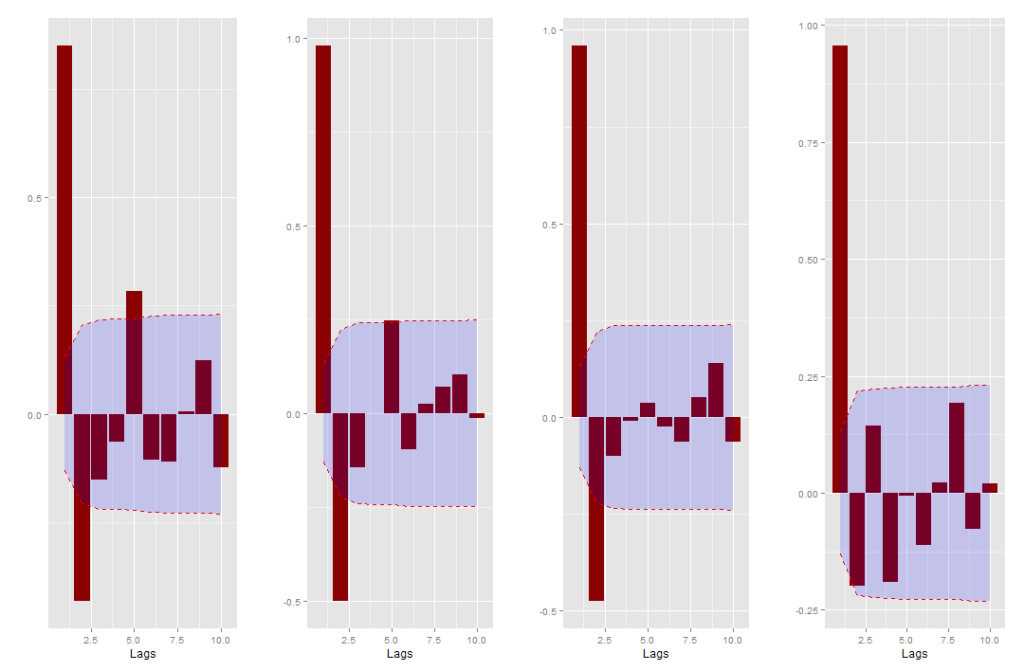
A seguir apresentamos as tabelas com as estatísticas descritas acima para os dois períodos de teste.

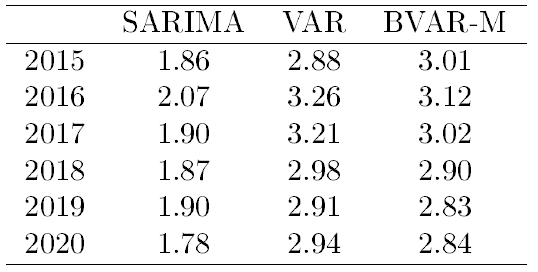
Como podemos ver, para o período mais curto os modelos mais complexos, segundo estas medidas, foram dominados pelo modelo mais simples que somente usa informação passada do próprio PIB. Porém, no longo prazo, esta tendência muda e os modelos que incorporam mais informação aparentam ser melhores.

Finalmente, apresentamos uma tabela com a previsão da taxa de crescimento do PIB americano para os próximos 5 anos segundo estes três modelos.

* Koop, G., & Korobilis, D. (2010). Bayesian multivariate time series methods for empirical macroeconomics. Now Publishers Inc.

** Hyndman, R. J., & Koehler, A. B. (2006). Another look at measures of forecast accuracy. International journal of forecasting, 22(4), 679-688.

Update: o script do R utilizado aqui e o arquivo com os dados aqui.