O pacote {modeltime} é um framework para modelagem e previsão de séries temporais no R, com a possibilidade de integração com o ecossistema do {tidymodels} para uso de técnicas de machine learning. O pacote promete ser uma interface veloz e moderna que possibilita prever séries temporais em grande escala (i.e. 10+ mil séries).
Utilizando uma interface simples e integrada com outros pacotes populares na linguagem, é possível construir uma ampla gama de modelos de previsão univariados e multivariados, tradicionais ou "modernos", dentre eles:
- ARIMA
- Suavização exponencial (ETS)
- Regressão linear (TSLM)
- Autoregressão de rede neural (NNETAR)
- Algoritmo Prophet
- Support Vector Machines (SVM)
- Random Forest
- Boosted trees
Neste exercício, daremos uma breve introdução aplicada exemplificando o fluxo de trabalho do {modeltime} para modelagem e previsão, além de fornecer nossa opinião sobre o mesmo. Para se aprofundar nos temas abordados nesse exercício, confira nossos Cursos de Econometria Aplicada.
Fluxo de trabalho
O fluxo de trabalho do pacote {modeltime} para criar um modelo de previsão de séries temporais pode ser resumido em 5 etapas:
- Colete e prepare os dados no ambiente do R;
- Separe amostras de treino/teste para avaliar modelos;
- Crie e estime múltiplos modelos de previsão;
- Avalie os modelos (resíduos, acurácia no teste, etc.);
- Reestime os modelos na amostra completa e gere previsões.
Com esse fluxo em mente, vamos agora realizar um exercício prático e didático: construir um modelo de previsão para a taxa de inflação brasileira, medida pelo IPCA (% a.m.) do IBGE. O objetivo é apenas demonstrar as ferramentas ( {modeltime}) de maneira prática no R, não estamos preocupados em criar o melhor modelo possível e nem em avaliar especificações profundamente. Para tal dê uma olhada nos cursos da Análise Macro.
Para reproduzir o exercício você precisará dos seguintes pacotes de R:
Passo 1: dados
Nesse exercício vamos criar modelos de previsão para o IPCA (% a.m.), portanto começamos por coletar e tratar os dados de maneira online diretamente do Sidra/IBGE (veja um tutorial neste link). Nossa amostra parte de 1999 e vai até o último dado disponível.
Abaixo criamos um gráfico de linha simples da série temporal do IPCA (% a.m.), do qual podemos observar uma flutuação em torno de 0,5% e um padrão sazonal, além de outliers (veja mais sobre análise exploratória neste link):
Passo 2: separar amostras
Com o objetivo de avaliar os modelos que criaremos em termos de acurácia da previsão pontual, vamos criar duas amostras da série temporal do IPCA: a de treino é usada para estimar um modelo especificado e gerar previsões com o mesmo e a de teste é usada para comparar as previsões geradas com os dados observados (verdadeiros). Nesse exercício vamos fazer essa separação em 95% para treino e o restante para teste:
Passo 3: modelagem
Como exemplo, vamos criar dois modelos univariados simples: família (auto) ARIMA e um passeio aleatório como benchmark. No {modeltime} a modelagem é feita em 3 etapas:
- Especificar o modelo (usando funções como arima_reg() e outras);
- Definir o pacote a ser usado (alguns modelos são implementados em mais de um pacote, e você tem flexibilidade em escolher qual usar com a função set_engine());
- Estimar o modelo (usando a função genérica fit(y ~ date, data = df), onde date não é um regressor, é apenas para uso interno do {modeltime}).
Note que, por esse fluxo de trabalho, o {modeltime} traz a vantagem de integrar em um único lugar diversos outros pacotes/modelos (consulte a documentação).
Os modelos ficam salvos como objetos do tipo lista no R e ao imprimi-los temos os principais resultados:
Passo 4: avaliar modelos
Uma vez que os modelos tenham sido estimados, vamos então investigar brevemente suas especificações: focaremos apenas em testar a normalidade e autocorrelação dos resíduos dos modelos estimados e em calcular as métricas MAE e RMSE dos pontos de previsão pseudo fora da amostra (comparando com a amostra de teste).
Para tais tarefas de diagnóstico de modelos o {modeltime} disponibiliza algumas funções úteis:
- modeltime_table() adiciona um ou mais modelos para criar uma "tabela de modelos";
- modeltime_calibrate() calcula os resíduos dos modelos;
- modeltime_residuals_test() aplica testes de normalidade/autocorrelação;
- modeltime_forecast() gera previsões;
- plot_modeltime_forecast() visualiza as previsões;
- modeltime_accuracy() calcula métricas de acurácia.
Vamos começar aplicando os testes de normalidade (Shapiro-Wilk) e autocorrelação (Box-Pierce e Ljung-Box) dos resíduos:
O resultado é uma tabela com os p-valores de cada teste, que indicam que os resíduos do modelo auto ARIMA, ao nível de 5% de significância, não são normalmente distribuídos e não apresentam autocorrelação. Para dados econômicos esses resultados são, em grande parte, comuns, de modo que iremos ignorar aqui o problema de normalidade e seguir adiante.
Agora vamos verificar a performance preditiva dos modelos nesse esquema pseudo fora da amostra. Para tal, primeiro juntamos os modelos em uma tabela de modelos e geramos n previsões fora da amostra, onde n é o número de observações da amostra de teste. Abaixo plotamos o gráfico das previsões geradas:
Pela avaliação visual os modelos estão muito aquém do desejado, mas esse exercício é apenas didático e, conforme mencionado, não estamos interessados em criar um "super" modelo que desempenhe melhor que as expectativas do Focus/BCB.
Em seguida, usamos a tabela de modelos para comparar os pontos de previsões gerados com os valores observados da amostra de teste, computado as métricas MAE e RMSE:
Como esperado, o modelo ARIMA apresenta um RMSE menor em relação ao benchmark, para o horizonte e amostra utilizados. Portanto, se fossemos decidir um modelo final entre os dois, a escolha seria pelo ARIMA. Note que em exercícios mais robustos o mais interessante é que você faça essa avaliação usando validação cruzada por horizontes de previsão (1, 2, 3, ..., meses a frente).
Passo 5: previsão
Com os modelos treinados e avaliados, o último passo é reestimar o(s) modelo(s) usando a amostra completa de dados para gerar previsões (efetivamente) fora da amostra. Use a função modeltime_refit() para tal:
E assim terminamos o fluxo de trabalho para modelagem e previsão com o {modeltime}. O que você achou do pacote?
Comentários
Como qualquer pacote/software, o {modeltime} tem suas vantagens e desvantagens, aqui vou pontuar a minha visão.
- Principais vantagens:
- Interface simples para iniciantes;
- Integra com o {tidymodels};
- Ecossistema ativo de desenvolvimento.
- Principais desvantagens:
- Interface fora do comum dos pacotes econométricos (i.e. fit(y ~ date, data = df));
- Documentação orientada a negócios/sem background estatístico;
- Tem cerca de 3x mais dependências (pacotes) do que concorrentes como o {fabletools};
- A comunidade de usuários é pequena (quando comparado pelo nº de perguntas no StackOverflow).
Em suma, se você é um iniciante o pacote {modeltime} deve ser ótimo para dar os primeiros passos no mundo de séries temporais e modelos de previsão, mas se você perguntar a uma pessoa mais experiente se esse é o pacote que ela prefere, provavelmente a resposta será não. Conforme você avança na área haverá a necessidade de ir além e essa lacuna provavelmente será preenchida por outro pacote. Contudo, se sua intenção não é mergulhar profundamente em séries temporais, basta instalar o pacote para começar usá-lo!
Saiba mais
Caso o assunto tenha despertado sua curiosidade, você pode se aprofundar nos tópicos com os cursos de Séries Temporais e Modelos Preditivos da Análise Macro.
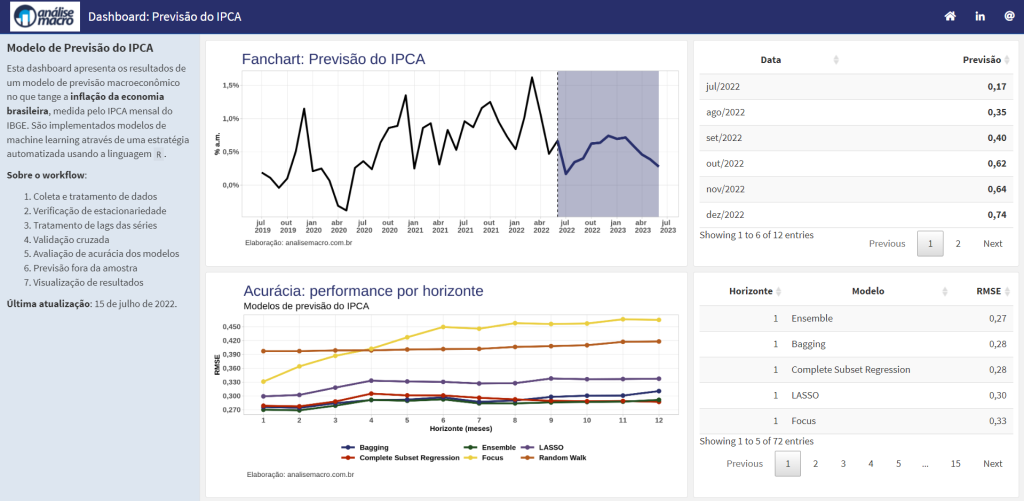
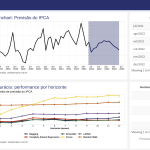
Como exemplo, no curso de Modelos Preditivos utilizamos modelos de machine learning para a previsão do IPCA. Os resultados são sumarizados nessa dashboard (clique para acessar), em uma abordagem automatizada:
Para se aprofundar nos temas abordados nesse exercício, confira nossos Cursos de Econometria Aplicada.