Efeito das Eleições sobre Ações de Estatais: aplicação do método event study

A teoria de finanças sugere que os mercados de capitais refletem nos preços das ações todas as informações disponíveis sobre as empresas. Dada essa premissa básica, pode-se estudar como um determinado evento — como as Eleições Ordinárias — impactava quantitativamente as ações de uma empresa. Para esse tipo de análise o método event study, que remonta aos estudos de Ball e Brown (1968) e Fama et al. (1969), pode ser empregado.

Na sua forma mais comum, que trataremos aqui, o método tenta medir o impacto de um evento específico nos retornos das ações, através do cálculo do chamado "retorno anormal" atribuído ao evento. Com base em uma janela de observações em torno do evento, o método estima quais devem ser os retornos normais da ação da empresa em análise. Com essa estimativa, o método calcula os "retornos anormais" atribuídos ao evento deduzindo os "retornos normais" dos "retornos observados". Os retornos normais precisam ser estimados e diferentes modelos podem ser especificados em uma análise de event study. Os modelos em si costumam ser usados também em outras áreas de pesquisa em finanças.

Uma vez que se tenha a métrica de interesse, os retornos anormais, prossegue-se com o desenho e aplicação de algum teste estatístico para verificar se o evento impacta os retornos da ação. Há vários testes paramétricos e não paramétricos propostos na literatura que podem ser usadas, a depender da especificação do estudo em questão.

Guia prático de implementação

Uma análise aplicada do método event study pode ser resumida nos seguintes procedimentos, conforme MacKinlay (1997):

1) Definir o evento: pode ser virtualmente qualquer tipo de acontecimento público que se deseja analisar o efeito no preços das ações. Alguns exemplos são:

• Eleições;
• Mudanças regulatórias;
• Divulgação de resultados;
• Eventos políticos.

2) Definir as empresas para análise: é necessário definir um critério de seleção para inclusão de uma empresa na análise. O critério pode ser com base em restrição de dados disponíveis ou em restrições como a representação em um determinado setor alvo do estudo. Por exemplo, se o objetivo é avaliar o efeito de um evento sobre as ações de empresas estatais brasileiras, então uma restrição poderia ser o número de empresas estatais listadas na B3.

3) Obter os dados das empresas: dados de cotação das ações das empresas são necessários para a análise, portanto é necessário empregar a coleta dos dados de alguma fonte confiável. Geralmente, análises de event study utilizam cotações diárias, dado que os eventos costumam ser melhor definidos nessa frequência. Procedimentos de coleta de dados são exemplificados no curso de R para o Mercado Financeiro da Análise Macro.

4) Definir a janela do evento: a definição do evento permite decidir a janela temporal de observações que serão analisadas. O objetivo é "dividir" a amostra de dados em algumas partes para adequação ao método.

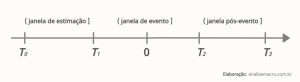
• Janela de estimação: amostra de dados utilizada para estimar o retorno normal, de T₀ + 1 na imagem abaixo. Essa amostra não se sobrepõe à próxima para não obter uma estimativa do retorno normal que seja influenciada pelos retornos próximos ao evento;
• Janela de evento: amostra de dados que define o evento e utilizada pra calcular os retornos anormais, sendo a data do evento definida como T = 0. Usualmente utiliza-se uma janela de evento de tamanho maior do que a data do evento, para capturar retornos anormais nessa "vizinhança" do acontecimento, de T₁ + 1 a T₂;
• Janela pós-evento: amostra de dados após o evento, quando o preço da ação da empresa "já absorveu" o evento, de T₂ + 1 a T₃. Pode ser usada para comparar, por exemplo, diferença de médias.

Com exceção da data do evento, não há regra geral para decidir entre a duração das janelas.

5) Mensuração do retorno normal e anormal: para avaliar o impacto do evento sobre o retorno das ações é necessário calcular o retorno anormal, que é o retorno observado na janela de evento menos o retorno normal esperado na janela de evento. O retorno normal é definido como o retorno esperado sem condicionar ao momento do evento. Sendo assim, podemos representar mais formalmente essa relação como:

RA_i,t = R_i,t - E(R_i,t|X_t)

onde:
i → empresa analisada;
t → data do evento;
RA_i,t → retorno anormal;
R_i,t → retorno observado;
E(R_i,t|X_t) → retorno normal;
X_t → é a informação condicionante para o modelo de retorno normal.

Essa abordagem implica, conforme já mencionado, que é necessário estimar o retorno normal. Para tal, existem algumas opções de modelos, alguns simples e outros mais complexos. Aqui vamos abordar brevemente 3 destes modelos de retorno normal.

5.a) Constant Mean Return Model: é uma especificação simples onde assume-se que o retorno normal é constante ao longo do tempo.

R_i,t = u_i + ε_i,t^a

onde:
u_i → é o retorno médio da ação da empresa i;
ε_i,t^a → é o termo de erro com média igual a zero e variância σ²_εi^a.

5.b) Market Model: é um modelo estatístico que explica o retorno normal introduzindo o retorno de mercado — geralmente representado por um índice de ações, como o IBOVESPA —, de forma a remover a fração do retorno que é relacionada à variação do retorno de mercado. Sendo assim, a variância do retorno anormal é reduzida.

R_i,t = α_i + β_i R_{m,t +} ε_i,t^b

onde:
α_i e β_i → são parâmetros do modelo para serem estimados;
R_m,t → é o retorno de mercado;
ε_i,t^b → é o termo de erro com média igual a zero e variância σ²_εi^b.

5.c) Capital Asset Pricing Model: é um modelo econômico onde o retorno esperado é determinado pela sua covariância com o portfólio de mercado.

R_i,t = R_f,t + β_i (E(R_m,t) - R_f,t)

onde:
R_f,t → é a taxa de juros livre de risco;
β_i → é um parâmetro estimado pelo modelo;
E(R_m,t) → é o retorno esperado de mercado.

6) Testes estatísticos: o último passo é testar estatisticamente se o evento impacta os retornos da ação, ou seja, a hipótese nula, H_{0 ,} é de que o evento não afeta a distribuição dos retornos. Há vários testes para várias representações dos retornos anormais (médios, acumulados, etc.). Alguns exemplos são:

• Paramétricos:
  • Brown and Warner test (1980/1985);
  • t-test;
  • Patell's test (1976);
  • Boehmer's test (1991);
  • Lamb's test (1995).
• Não paramétricos:
  • Simple binomial sign test;
  • Generalized binomial sign test;
  • Corrado's sign test (1992);
  • Rank test/modified rank test;
  • Wilcoxon signed rank test.

Exemplo no R

Vamos exemplificar o método para tentar responder a provocação do título deste exercício: será que as eleições afetam as ações de empresas estatais no Brasil?

Com base no método event study, sumarizamos a seguir informações gerais para a construção do exercício:

1) Definir o evento: os eventos são as datas de Eleições Ordinárias nacionais brasileiras, referente aos anos de 2010, 2014 e 2018, considerando apenas o primeiro turno;
2) Definir as empresas para análise: selecionamos livremente uma amostra de empresas "estatais" listadas na B3, quais sejam, Banco do Brasil (BBAS3), Petrobras (PETR4) e Telebras (TELB4);
3) Obter os dados das empresas: os dados de preços de cotação de fechamento foram obtidos do Yahoo Finance — uma base de dados de acesso público —, na frequência diária;
4) Definir a janela do evento: definiu-se como janela de estimação 250 observações anteriores a janela de evento, esta contendo 20 observações (10 antes da data da eleição e 10 após o evento);
5) Mensuração do retorno normal e anormal: optou-se pelo modelo mais comum, o Market Model, utilizando o IBOVESPA como índice de ações para o termo de retorno de mercado;
6) Testes estatísticos: optou-se pela estratégia de aplicar diferentes testes paramétricos e não paramétricos para o mesmo conjunto de eventos/empresas analisadas.

Utilizamos o pacote {estudy2} no R para aplicação do método, ver Rudnytskyi (2021). A seguir apresentamos os resultados (códigos de replicação disponíveis para membros do Clube AM da Análise Macro).

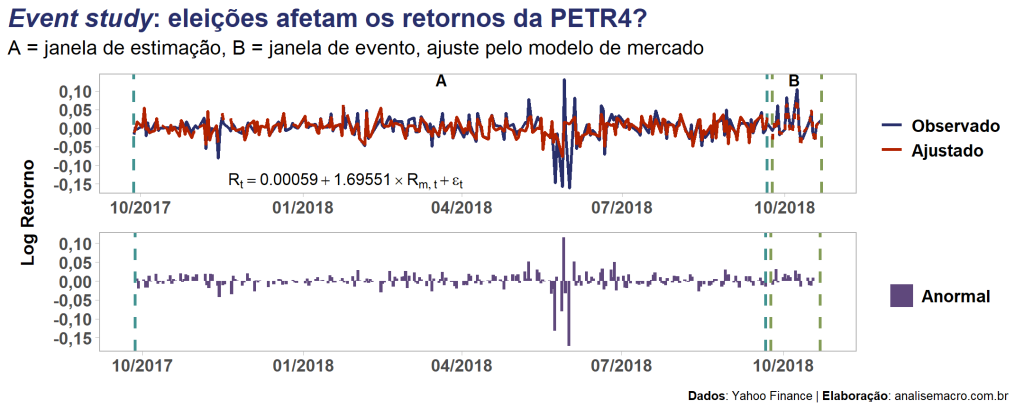
O gráfico abaixo apresenta o "passo a passo" resumido do método event study para apenas uma das empresas (PETR4) deste exercício, por simplificação visual. A linha azul representa o log retorno observado da ação para ambas as janelas (estimação e evento). Pelo Market Model, utiliza-se o log retorno da janela de estimação (A) para inferir (observar os parâmetros estimados pelo modelo no primeiro painel) o log retorno esperado na janela de evento (B). Com isso é possível obter o retorno anormal, representado pelas colunas em roxo no segundo painel.

Note que parece haver outliers na janela de estimação — que se refere ao evento "Eleição 2018" —, o que pode ser problemático para o método de estimação (MQO) do modelo e para os testes estatísticos, apresentados a seguir.

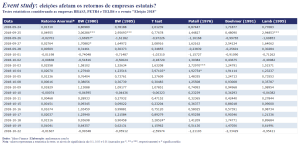
A tabela abaixo apresenta os resultados de diversos testes paramétricos aplicados ao exercício em questão, referente apenas ao evento "Eleição 2018", por simplificação visual (para os demais eventos considerados os resultados são semelhantes). Os valores críticos são da distribuição t de Student, exceto de Patell e Lamb que utilizam a distribuição normal, e os asteriscos refletem o nível de significância encontrados para um dado dia da janela de evento. Os testes são aplicados automaticamente pelo pacote {estudy2}, apesar de nem todos servirem ao propósito do exercício (como BW (1980), que é desenhado para dados mensais). Em geral, os testes examinam como hipótese se o valor esperado para um determinado dia é igual a zero. Veja referências sobre os testes na documentação do pacote.

Percebe-se, para a maioria dos testes aplicados, que há poucos retornos anormais médios significativos na janela de evento e, quando há, são positivos. Além disso, estes retornos anormais encontrados como significativos são, em geral, prévios à data do evento (neste caso, eleição ocorreu no dia 07/10/2018). Estes resultados são semelhantes para os demais eventos analisados (eleição de 2010 e 2014), apesar de serem "dispersos", no sentido de que na janela de evento predominam resultados não significativos.

Concluo que uma investigação mais aprofundada sobre a temática do exercício seria apropriada para compreender melhor a questão referente a eleições e ações de empresas estatais.

Saiba mais

Para saber mais sobre dados eleitorais, R, Python, programação e análise de dados faça parte do Clube AM e confira o curso de Microdados Brasileiros, onde tratamos de dados eleitorais e vários outros.

Códigos de replicação deste exercício estão disponíveis para membros do Clube AM.

Na semana passada mostramos como coletar e tratar dados eleitorais e na próxima semana aplicaremos uma análise de sentimentos com a temática eleitoral, não perca!

Referências

Ball, R., & Brown, P. (1968). An empirical evaluation of accounting income numbers. Journal of accounting research, 159-178.

Fama, E. F., Fisher, L., Jensen, M. C., & Roll, R. (1969). The adjustment of stock prices to new information. International economic review, 10(1), 1-21.

MacKinlay, A. C. (1997). Event studies in economics and finance. Journal of economic literature, 35(1), 13-39.

Rudnytskyi, I. (2021). estudy2: An Implementation of Parametric and Nonparametric Event Study. R package version 0.10.0, https://CRAN.R-project.org/package=estudy2.