Seleção de carteira e Teoria de Markowitz

A avaliação de carteiras de investimentos envolve três grandes fases de estudo: análise dos títulos, análise das carteiras e seleção da carteira. Estaremos aqui focamos no processo de seleção de carteira e utilizaremos o método desenvolvido por Harry Markowitz. Fazemos o uso do Python como ferramenta para obter os dados de ações e estimar os parâmetros e combinações da carteira de investimento ótima.

Vimos, graficamente, o que acontece com o retorno e o risco quando combinamos os ativos. O nome do gráfico gerado em cada caso é Conjunto de Oportunidade de Investimento. Isto é, ele representa combinações de diferentes pesos de investimento em cada um dos dois ativos na dimensão retorno x risco.

1. Carregamento de bibliotecas


import numpy as np
import pandas as pd
import yfinance as yf
from plotnine import *
import seaborn as sns
sns.set()

2. Coleta e tratamento de dados

# Display para formato em %
pd.options.display.float_format = '{:.4%}'.format

# Período
start = '2016-01-01'
end = '2022-12-30'

# Tickers dos ativos
assets = ['BBDC4.SA', 'ITSA4.SA', 'GGBR4.SA', 'WEGE3.SA']

# Baixa os dados (dados mensais)
data = yf.download(assets, start = start, end = end, interval = '1mo')
data = data.loc[:,('Adj Close', slice(None))]
data.columns = assets
<pre>

# Calculando os retornos
Y = data[assets].pct_change().dropna()

# Verifica os retornos mensais
display(Y.head())

Código

	BBDC4.SA	ITSA4.SA	GGBR4.SA	WEGE3.SA
Date
2016-02-01	17.6934%	-1.9445%	-0.8721%	-14.6831%
2016-03-01	26.9335%	85.2692%	23.1514%	7.1198%
2016-04-01	5.3757%	19.4190%	6.2313%	8.4479%
2016-05-01	-11.9086%	-28.6812%	-9.3072%	-5.2042%
2016-06-01	10.5213%	5.7451%	6.3026%	-4.5170%

Conjunto de Oportunidades

A seleção de carteiras procura identificar a melhor combinação possível de ativos, obedecendo às preferências do investidor com relação ao risco e retorno esperados. Dentre as inúmeras carteiras que podem ser formadas com os ativos disponíveis, é selecionada aquela que maximiza seu grau de satisfação.

Aqui, identificamos grau de satisfação aquela em que obtém-se a carteira que: - Minimiza o risco, dentre todas as combinações; - Maximiza o retorno, dentre todas as combinações; - Maximiza a medida de retorno ajustado ao risco; - Maximiza a utilidade do investidor.

Para saber como podemos escolher essas carteiras, vamos construir um Conjunto de Oportunidades para os ativos que coletamos os dados e calculamos os retornos simples.

A pergunta relevante aqui é: Qual combinação de Portfólio escolher? Isto é, qual ponto (combinação de pesos) representado no gráfico devemos escolher?

A decisão ficará de certa forma um pouco subjetiva, visto que cada investidor possui uma aversão ao risco, e se propõe a obter mais retorno e troca de mais risco.

Entretanto, podemos pensar no principio da dominância: é válido escolher combinações que façam sentido, na proposição de que, caso haja uma combinação que tenha o mesmo retorno, mas riscos diferentes, se escolhe aquele em que possui o mesmo nível de retorno (ou maior) a um menor nível de risco.

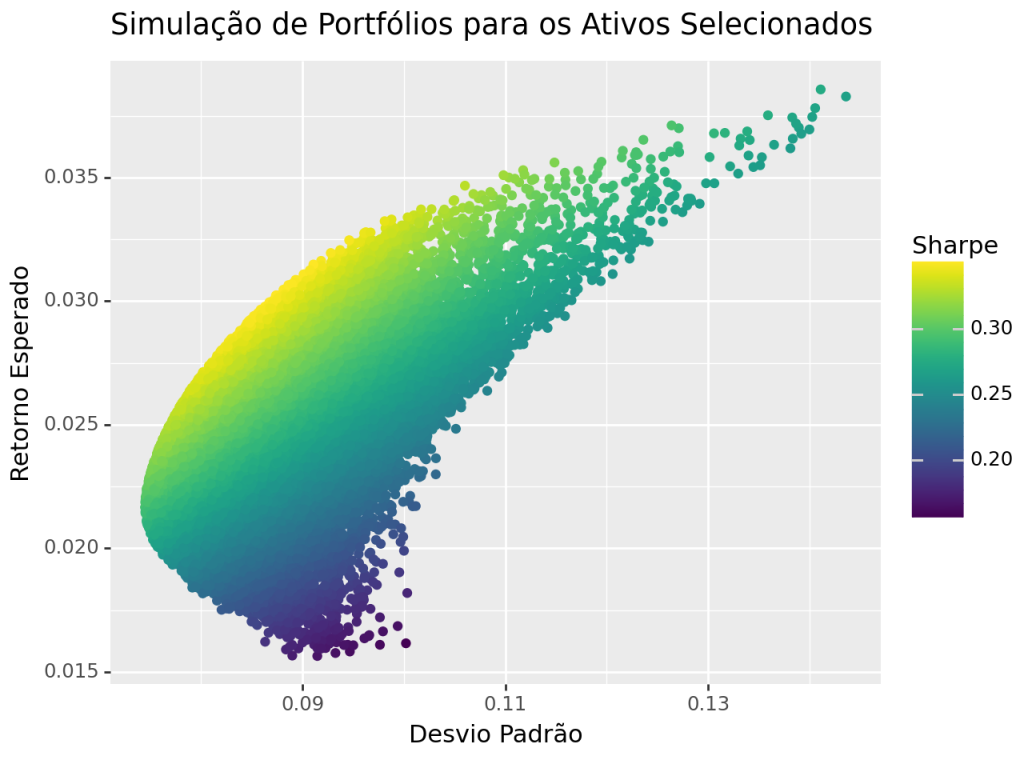
# calcula o retorno esperado
mu = Y.mean()
# calcula a matriz de covariância
cov_matrix = Y.cov()

# número de portfólio (número de pesos aleatórios gerados)
num_portfolios = 25000

# cria um array para manter os resultados
results = np.zeros((3,num_portfolios))

# cria o for loop para as simulações
for i in range(num_portfolios):
# seleciona pesos aleatórios para os portfólios
weights = np.random.random(4)

# verifica se os portfólios somam 1
weights /= np.sum(weights)

# calcula os retornos esperado do portfólio
portfolio_return = np.sum(mu * weights)
# calcula a volatilidade
portfolio_std_dev = np.sqrt(np.dot(weights.T,np.dot(cov_matrix, weights)))

# armazena os valores no array
results[0,i] = portfolio_return
results[1,i] = portfolio_std_dev

# Calcula o Sharpe Ratio (retorno / volatilidade) - sem taxa livre de risco
results[2,i] = results[0,i] / results[1,i]

# Converte o resultado para um df
results_frame = pd.DataFrame(results.T, columns = ['Retorno Esperado','Desvio Padrão','Sharpe'])
<pre># Cria o gráfico de dispersão com barra para o Sharpe
(ggplot(results_frame, aes(x = 'Desvio Padrão', y = 'Retorno Esperado', color = 'Sharpe'))
+ geom_point()
+ labs(title = "Simulação de Portfólios para os Ativos Selecionados")
)

No gráfico acima criamos diversas carteiras com uma simulação de 25000 portfólios diferentes. São apenas algumas das possíveis carteiras que poderiam ser formadas com os ativos em questão. Veja que cada uma resulta em uma combinação diferente para risco e retorno. A possibilidade de menor obtenção de menor risco no plano é resultado de ativos que possuem correlação baixa ou mesmo negativa, reduzindo o risco da carteira a um nível menor que o do ativo individual.

Fronteira Eficiente

A seleção da carteira de investimento mais atraente para um investidor racional, que avalia a relação risco/retorno em suas decisões, fica restrita às combinações disponíveis no trecho da linha de combinações descrita no gráfico acima. Esse segmento, conhecido por fronteira eficiente, insere todas as carteiras possíveis de serem construídas.

A fronteira eficiente restringe o conjunto de oportunidades para somente poucos títulos.

Isso porque o investidor racional deverá escolher aquela combinação que maximiza o retorno esperado para um menor nível possível de risco ou, em outras palavras, a que promove o menor risco para um dado retorno esperado. As alternativas de investimento que atendem a essa orientação são aquelas dispostas ao longo da linha vermelha tracejada, e são denominadas por Markowitz de eficientes.

A escolha da melhor carteira é determinada, uma vez mais, pela postura demonstrada pelo investidor em relação ao dilema risco/retorno presente na avaliação de investimentos.

A partir da Fronteira Eficiente só é possível aumentar o retorno aumentando o risco – compatível com a teoria clássica de finanças – por isso ela é chamada de eficiente.

Como montamos obtemos a melhor carteira?

Vamos elencar duas formas de obtermos as melhores carteiras de investimento do nosso Conjunto de Oportunidades de forma a abarcamos as preferências do investimento. A que possuí risco mínimo e máximo retorno.

No caso em que não são permitidas vendas à descoberto e nem empréstimos, temos as seguintes restrições;

a soma das proporções alocadas em cada ativo tem que ser igual a um;
cada ativo tem que ter peso maior ou igual a zero;
em cada problema escolhemos um retorno esperado para o qual minimizaremos o risco.

Carteira de Variância Mínima

Para marcar um ponto na fronteira eficiente, escolhemos um nível de retorno e resolvemos o problema de minimização de risco.

Formalmente, o problema de otimização para cada ponto do gráfico é:

$min_{w_i} \ \ \sum_{j=1}^N(w_j^2 \sigma_j^2)+\sum_{j=1}^N\sum_{\substack{k=1 \\ k \neq j}}^N(w_j w_k \sigma_{jk})$

s.a.

- $\sum_{j=1}^N w_j = 1$

- $w_j \geq 0, \forall i$

- $\sum_{j=1}^N w_i\bar{R}_j = \bar{R}_p$

Carteira de Máximo Retorno

Para marcar um ponto na fronteira eficiente, resolvemos o problema de maximização de retorno:

$max_{w_i} \ \ E(R_p)=\sum_{i=1}^N(w_{i}E(R_i))$

s.a.

- $\sum_{j=1}^N w_j = 1$

- $w_j \geq 0, \forall i$

- $\sum_{j=1}^N w_i\bar{R}_j = \bar{R}_p$

Os pontos gerados da Carteira de Variância Mínima até a Carteira de Máximo Retornos que representam a Fronteira Eficiente do Conjunto de Oportunidades.

3. Otimização de Carteira com riskfolio

Para produzir nossas carteiras ótimas, vamos fazer o uso da biblioteca riskfolio, que permite obtermos ferramentas para a construção de carteiras com a escolha de diversas medidas para:

- Retorno esperado;

- Risco;

- Restrições;

- Gráficos e tabelas;

- Entre diversas ferramentas.

Construímos um código abaixo para nossa carteira de mínima variância.

# Instala e carrega a biblioteca
!pip install riskfolio-lib
import riskfolio as rp

3.2 Carteira de Mínima Variância

# Construindo o objeto de portfólio
port = rp.Portfolio(returns = Y)

# Calculando o portfólio ótimo
# Selecionar método e estimar parâmetros de entrada:
method_mu = 'hist' # Método para estimar retornos esperados com base em dados históricos.
method_cov = 'hist' # Método para estimar a matriz de covariância com base em dados históricos.

# Cria os inputs
port.assets_stats(method_mu = method_mu, method_cov = method_cov)

# Estimando o portfólio ótimo:
model = 'Classic' # Pode ser Classic (histórico), BL (Black Litterman) ou FM (Modelo de Fatores)
rm = 'MV' # Medida de risco usada, mean-variance. Há possibilidade de diversas outras medidas de risco, checar documentação.
obj = 'MinRisk' # Função objetivo, pode ser MinRisk, MaxRet, Utility ou Sharpe
hist = True # Usar cenários históricos para medidas de risco que dependem de cenários
rf = 0 # Taxa livre de risco
l = 0 # Fator de aversão ao risco, útil apenas quando obj é 'Utility'

# Otimização do portfólio
w = port.optimization(model = model, rm = rm, obj = obj, rf = rf, l = l, hist = hist)

# Verifica os pesos
display(w.T)

Código

	BBDC4.SA	ITSA4.SA	GGBR4.SA	WEGE3.SA
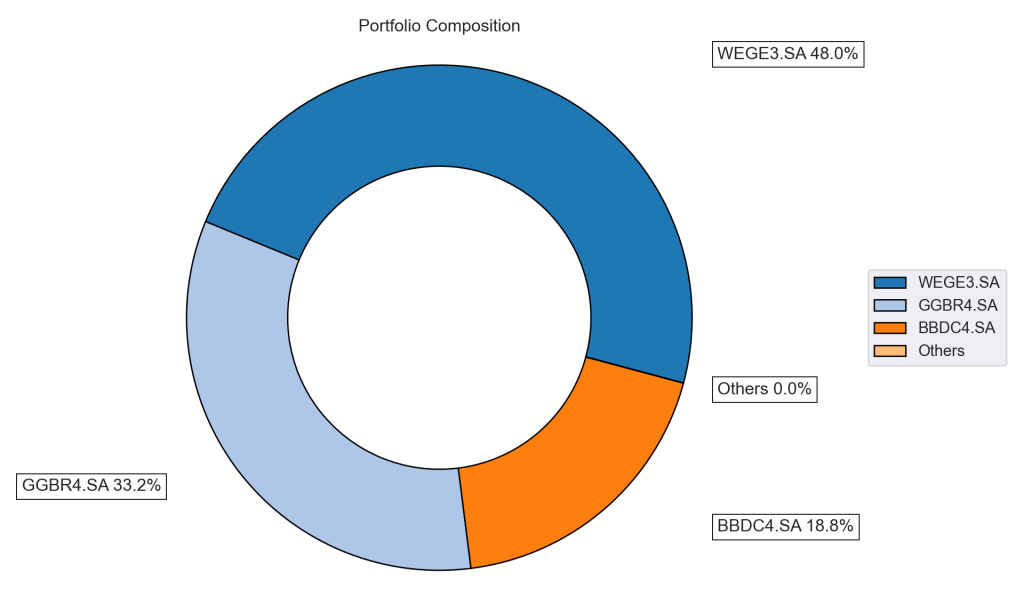
weights	18.8353%	0.0000%	33.2142%	47.9506%


# Gerando a fronteira eficiente
points = 50 # Número de pontos da fronteira

# Cria a variável da fronteira
frontier = port.efficient_frontier(model = model, rm = rm, points = points, rf = rf, hist = hist)

# Verifica as combinações
display(frontier.T.head())

Código

	BBDC4.SA	ITSA4.SA	GGBR4.SA	WEGE3.SA
0	18.8353%	0.0000%	33.2142%	47.9506%
1	23.1562%	5.8873%	14.6367%	56.3198%
2	24.0765%	9.7665%	7.1314%	59.0256%
3	24.8541%	12.8357%	1.1300%	61.1802%
4	21.8258%	15.8984%	0.0001%	62.2757%

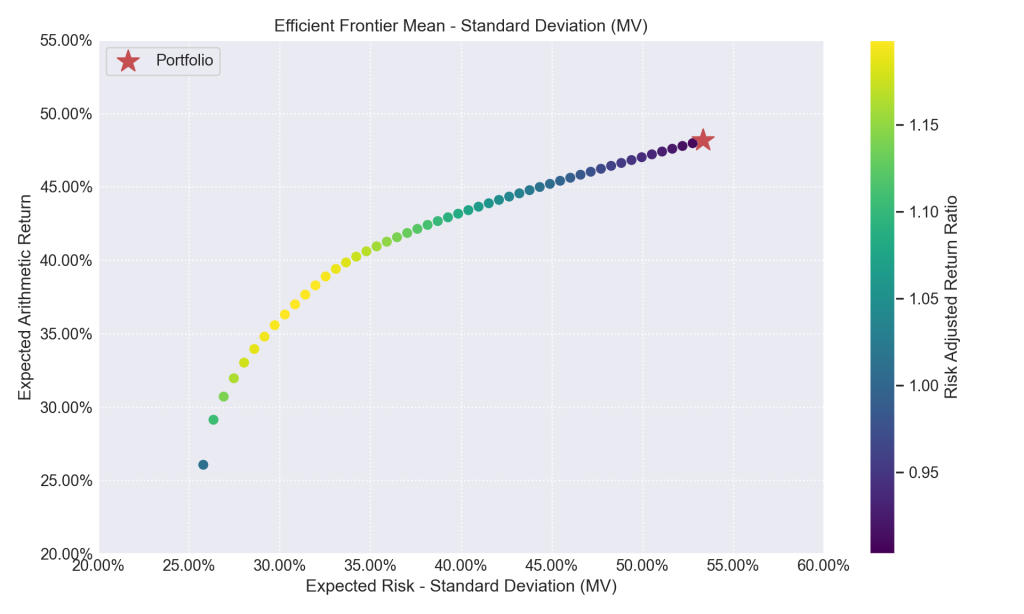
# Plotando a fronteira eficiente
mu = port.mu # Retorno Esperado
cov = port.cov # Matriz de Covariância
returns = port.returns # Retorno dos ativos

# Cria o gráfico
ax = rp.plot_frontier(w_frontier=frontier, mu=mu, cov=cov, returns=returns, rm=rm,
rf=rf, alpha=0.05, cmap='viridis', w=w, s=16, c='r', height=6, width=10, ax=None, t_factor = 12)
<pre>

A Fronteira Eficiente são os pontos marcado no gráfico acima, que fazem parte do Conjunto de Oportunidade de Investimento (COI) que começa na carteira de variância mínima e vai até a carteira de retorno máximo (todo investimento no ativo de maior retorno).

A carteira de variância mínima é interessante não só teoricamente (por definir o início da Fronteira), como também na prática, pois ela define a combinação de ativos que gera a carteira eficiente com menor risco.

A carteira de variância mínima é a que tem menor risco. Ela fica na extremidade esquerda do COI, onde começa a Fronteira Eficiente.

Podemos verificar também os pesos dos ativos que compõem a carteira de variância mínima.

# Plota a composição do Portfólio
ax = rp.plot_pie(w = w, others=0.05, nrow=25, cmap = "tab20",
height=6, width=10, ax=None)

Ou seja, caso o investidor deseja obter uma carteira com o menor risco possível, deverá escolher a combinação acima (isto não é uma recomendação de investimento).

3.2 Carteira de Máximo Retorno

Vamos agora construir a carteira de máximo retorno usando a biblioteca riskfolio.


# Construindo o objeto de portfólio
port = rp.Portfolio(returns = Y)

# Calculando o portfólio ótimo
# Selecionar método e estimar parâmetros de entrada:
method_mu = 'hist' # Método para estimar retornos esperados com base em dados históricos.
method_cov = 'hist' # Método para estimar a matriz de covariância com base em dados históricos.

# cria as estatísticas
port.assets_stats(method_mu = method_mu, method_cov = method_cov, d = 0.94)

# Estimando o portfólio ótimo:
model = 'Classic' # Pode ser Classic (histórico), BL (Black Litterman) ou FM (Modelo de Fatores)
rm = 'MV' # Medida de risco usada, mean-variance (média-variância)
obj = 'MaxRet' # Função objetivo, pode ser MinRisk, MaxRet, Utility ou Sharpe
hist = True # Usar cenários históricos para medidas de risco que dependem de cenários
rf = 0 # Taxa livre de risco de mesmo período da janela dos ativos
l = 0 # Fator de aversão ao risco, útil apenas quando obj é 'Utility'

# Otimização do portfólio
w = port.optimization(model = model, rm = rm, obj = obj, rf = rf, l = l, hist = hist)

# Verifica os pesos
display(w.T)

	BBDC4.SA	ITSA4.SA	GGBR4.SA	WEGE3.SA
weights	0.0000%	100.0000%	0.0000%	0.0000%

# Gerando a fronteira eficiente
points = 50 # Número de pontos da fronteira

# Cria a variável da fronteira
frontier = port.efficient_frontier(model = model, rm = rm, points = points, rf = rf, hist = hist)

# Verifica as combinações
display(frontier.T.head())
<pre>

	BBDC4.SA	ITSA4.SA	GGBR4.SA	WEGE3.SA
0	18.8353%	0.0000%	33.2142%	47.9506%
1	23.1562%	5.8873%	14.6367%	56.3198%
2	24.0765%	9.7665%	7.1314%	59.0256%
3	24.8541%	12.8357%	1.1300%	61.1802%
4	21.8258%	15.8984%	0.0001%	62.2757%

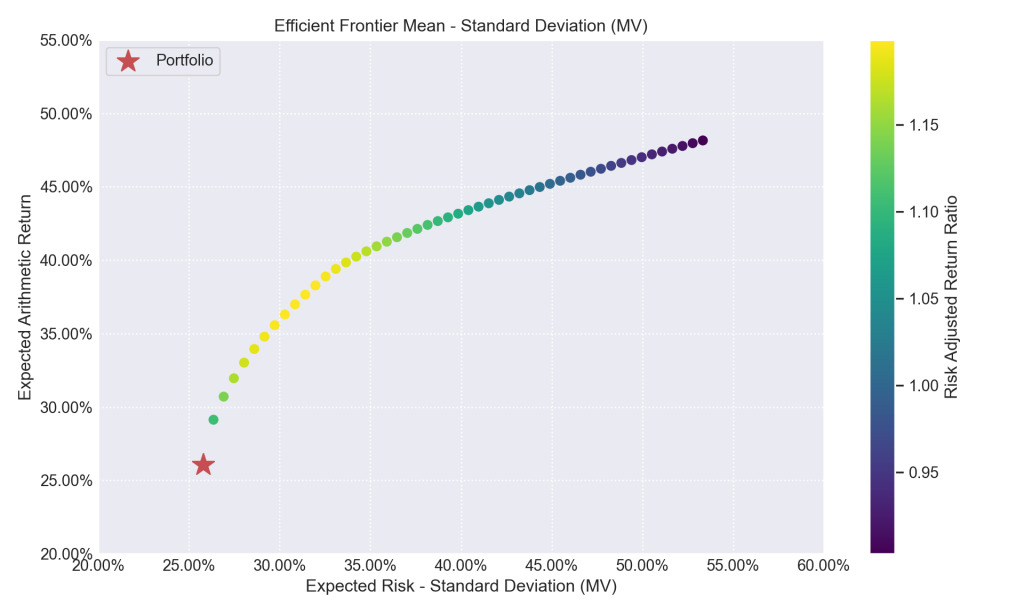
# Plotando a fronteira eficiente
mu = port.mu # Retorno Esperado
cov = port.cov # Matriz de Covariância
returns = port.returns # Retorno dos ativos

# Cria o gráfico
ax = rp.plot_frontier(w_frontier = frontier, mu = mu, cov = cov, returns = returns, rm = rm,
rf=rf, alpha=0.05, cmap='viridis', w=w, s=16, c='r', height=6, width=10, ax=None, t_factor = 12)

No gráfico acima verificamos o ponto da combinação que obtemos o portfólio de retorno máximo. Obviamente tal combinação é a que possui maior risco.

Referências

A. A. Neto. Mercado Financeiro. Editora Atlas, 2012.

E. J. Elton et al. Moderna Teoria de Carteiras e Análise de Investimentos. Editora Elsevier, 2010

Quer aprender mais?

- Cadastre-se gratuitamente aqui no Boletim AM e receba toda terça-feira pela manhã nossa newsletter com um compilado dos nossos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas;

- Quer ter acesso aos códigos, vídeos e scripts de R/Python desse exercício? Vire membro do Clube AM aqui e tenha acesso à nossa Comunidade de Análise de Dados;

- Quer aprender a programar em R ou Python com Cursos Aplicados e diretos ao ponto em Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas? Veja nossos Cursos aqui.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise exploratória para modelagem preditiva no Python

Como usar modelos do Sklearn para previsão? Uma introdução ao Skforecast

Métodos de Reamostragem de Séries Temporais no Python

Coletando dados regionais do CAGED no Python

Coletando dados de Setores Censitários do Censo 2022 no Python

Estimando a inércia inflacionária através de modelos de espaço-estado usando Python

Outros artigos relacionados

Análise exploratória para modelagem preditiva no Python

Antes de desenvolver bons modelos preditivos é necessário organizar e conhecer muito bem os dados. Neste artigo, damos algumas dicas de recursos, como gráficos, análises e estatísticas, que podem ser usados para melhorar o entendimento sobre os dados usando Python.

Como usar modelos do Sklearn para previsão? Uma introdução ao Skforecast

Prever séries temporais é uma tarefa frequente em diversas áreas, porém exige conhecimento e ferramentas específicas. Os modelos de machine learning do Sklearn são populadores, porém são difíceis de aplicar em estruturas temporais de dados. Neste sentido, introduzimos a biblioteca Skforecast, que integra os modelos do Sklearn e a previsão de séries temporais de forma simples.

Métodos de Reamostragem de Séries Temporais no Python

Nesta postagem, vamos mostrar alguns métodos simples para lidar com a reamostragem de dados de séries temporais no Python.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!