A partir dessa semana, começaremos, o Ricardo Lima e eu, a publicar uma série de posts referentes à inflação no Brasil. Desde os tempos em que criei, em conjunto com um time enorme, o GECE/UFF, percebi que existe uma grande dificuldade de estudantes de graduação e pós-graduação de integrar teoria com a prática dos dados. Desse modo, são dois os objetivos dessa série: (i) mostrar, de forma bem introdutória, como lidar com dados macroeconômicos na prática, usando o software R; (ii) entender o comportamento da taxa de variação dos preços no país, bem como gerar alguns modelos de previsão para a inflação, dados seus determinantes. Ademais, servirá como incentivo para deslanchar: (i) um projeto de previsões sofisticadas de variáveis macroeconômicas utilizando o R que estamos desenvolvendo, em conjunto com o Renato Lerípio; (ii) um curso de análise de conjuntura para graduandos e pós-graduandos em diferentes áreas. Para quem quiser, antes de tudo, conferir o que é inflação, pode dar uma olhada aqui e ouvir um podcast sobre o assunto aqui.
Para tornar as coisas didáticas, começarei bem do início, de modo que mesmo o leitor com poucos conhecimentos de economia, estatística, econometria e/ou manipulação de dados poderá ter a exata noção do que foi feito. Nesse primeiro post, apresentarei os diversos índices de inflação no país, bem como darei as primeiras pistas sobre o que está causando a inflação alta que temos visto. Leitores com conhecimentos mais avançados podem pular as partes mais introdutórias e partir para a análise mais técnica dos problemas. Sempre que possível colocaremos referências sobre os assuntos que abordarmos [quem tiver outras, pode colocar nos comentários]. Sugestões, críticas [construtivas!!!] e comentários diversos são sempre bem vindos. Se a coisa fluir da forma que esperamos, outras variáveis, como câmbio, pib, juros, ..., também poderão ganhar séries no mesmo formato. Para quem ainda não conhece o R, sugerimos ler aqui, aqui e aqui. Ao trabalho, então?
Antes de tudo, algumas noções básicas...
O aluno que sai da faculdade de economia tem grandes dificuldades de lidar com dados [o leitor mais avançado pode pular essa parte e continuar abaixo, quando vir um novo alerta desse mesmo tipo]. Soa forte a frase? Talvez você discorde disso e dê uma infinidade de exemplos contrários, mas minha experiência pessoal mostra que isso é uma espécie de verdade inconveniente. Em geral, os professores estão focados em ensinar a teoria - alguns, a ensinar o aperto de mão secreto - e deixam ao largo o confronto com os dados. Se é assim, a primeira coisa a fazer em uma série que tem a pretensão de fazer um raio-x da inflação no Brasil é mostrar as fontes de dados. Elas são basicamente quatro: Banco Central, FGV, IBGE e IPEADATA. O leitor encontrará uma infinidade de dados nesses lugares, não apenas de inflação, logo fique à vontade para navegar e se interar com os mesmos.
Minha sugestão é que você, depois de ter lido esse texto aqui, pegue o número índice de um único indicador em uma dessas fontes e comece a brincar com ele. Vamos supor que você tenha pego o número índice do IPCA no IPEADATA e queira obter a variação mensal e a variação anual dos preços. Primeiro, salve a planilha com o dado no seu computador e abra o R para importar os dados. Você deverá colocar o seguinte código para importar:
## Importação da planilha com o IPCA data <- ts(read.csv(file='ipca.csv',header=T,sep=";",dec=","), start=c(1979,12), freq=12)
Feito isto, você pode dar uma olhada no gráfico da série [com o plot], coisa que fiz no post sobre introdução à inflação, e pode também obter a variação mensal e anual com os seguintes comandos:
ipcamensal <- (data/lag(data,-1)-1)*100 ipcaanual <- (data/lag(data,-12)-1)*100
Dê uma olhada nos gráficos dessas duas séries que você acabou de criar acima utilizando o código abaixo. Repare que limitei os gráficos para o período entre 1999 e 2015, mas você pode escolher outros períodos.
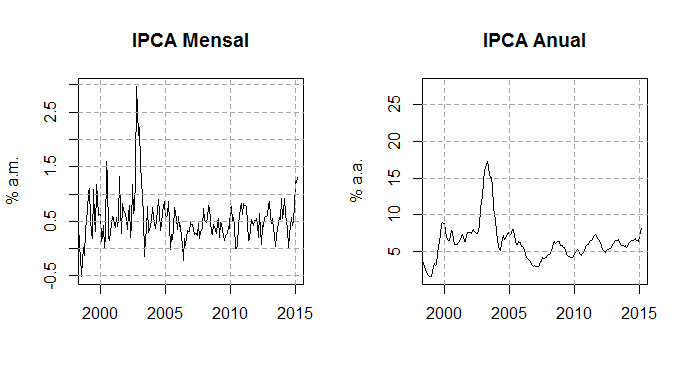
par() op <- par() lay <- layout(matrix(c(1,2), ncol=2, nrow=1, byrow=F)) layout.show(lay) plot(ipcamensal,main='IPCA Mensal',xlab='',ylab='% a.m.') grid(lty=2, lwd=1, col='darkgrey') plot(ipcaanual,main='IPCA Anual',xlab='',ylab='% a.m.') grid(lty=2, lwd=1, col='darkgrey')
O IPCA mensal reflete a variação de preços entre um e outro mês, como exposto na fórmula em que geramos a série. Já o IPCA anual é a variação acumulada em 12 meses. Observe que no período recente, a inflação acumulada em 12 meses tem tido uma tendência altista. Além dos gráficos, você pode obter algumas estatísticas descritivas com a função stat.desc do pacote pastecs, como mínimo, máximo, média, mediana, ou, mais simplesmente, com a função summary.
Agora que você já tem alguma familiaridade com os dados [o leitor mais avançado pode continuar daqui], podemos importar um conjunto mais amplo de índices, como os IGPs da FGV [com seus determinantes: IPA, IPC e INCC] e o próprio IPCA. Com esse conjunto maior de dados, podemos começar a entender o comportamento dos preços nos últimos tempos no país. Algumas brincadeiras interessantes também podem ser feitas, como a criação de núcleos próprios, que excluem, por exemplo, a tão falada inflação de serviços. Vamos, então?
Uma overdose de inflação...
Na minha planilha eu coloquei os três IGPs (10, M e DI), seus determinantes (IPA, IPC e INCC), o IPCA e o IPCA-15 - fica a seu critério quais vai querer colocar. Para, em primeiro lugar, dar uma olhada nos números mais atuais da inflação no país eu montei o script no R de modo a obter a variação mensal e anual de todos os índices, conforme os comandos que coloquei acima. Depois agrupei as variações mensais e anuais de forma a criar uma espécie de "tabela resumo" com as últimas três observações de cada índice de inflação. Isso foi feito com os seguintes códigos:
## As últimas três observações
last.mensal <- c('Mensal Fev/15', 'Mensal Mar/15', 'Mensal Abr/15')
last.anual <- c('Anual Fev/15', 'Anual Mar/15', 'Anual Abr/15')
data <- ts(read.csv(file='agregado.csv',header=T,sep=";",dec=","),
start=c(1994,07), freq=12)
######### Variações Mensais a partir dos números índices ###########
## Obter as variações mensais
vmensal <- (data/lag(data,-1)-1)*100
colnames(vmensal) <- paste0(colnames(data),'mensal')
## Colocar as últimas observações das séries mensais no mesmo objeto
mensal <- t(tail(vmensal, n = 3))
colnames(mensal) <- last.mensal
######### Variações Anuais a partir dos números índices ###########
## Obter as variações anuais
vanual <- (data/lag(data,-12)-1)*100
colnames(vanual) <- paste0(colnames(data),'anual')
## Colocar as últimas observações das séries anuais no mesmo objeto
anual <- t(tail(vanual,3))
colnames(anual) <- last.anual
############### CRIAR TABELA COM ÚLTIMAS OBSERVAÇÕES ##################
agregado <- round(cbind(mensal, anual), digits=2)
rownames(agregado) <- colnames(data)
################### GERAR CÓDIGO HTML ################################ table <- stargazer(agregado, title='Índices de Inflaçao no Brasil (%)', type='html', out='agregado.html', decimal.mark=',', digits=2, align=T)
E a tabela...
| Mensal Fev/15 | Mensal Mar/15 | Mensal Abr/15 | Anual Fev/15 | Anual Mar/15 | Anual Abr/15 | |
| igp10 | 0,43 | 0,83 | 1,27 | 3,86 | 3,38 | 3,46 |
| ipa10 | 0,03 | 0,75 | 1,45 | 2,13 | 1,23 | 1,27 |
| ipc10 | 1,39 | 1,29 | 1,01 | 7,56 | 8,19 | 8,33 |
| incc10 | 0,80 | 0,24 | 0,69 | 6,77 | 6,69 | 7,01 |
| igpm | 0,27 | 0,98 | 1,17 | 3,86 | 3,16 | 3,55 |
| ipam | -0,09 | 0,92 | 1,41 | 2,02 | 0,75 | 1,36 |
| ipcm | 1,14 | 1,42 | 0,75 | 7,74 | 8,39 | 8,31 |
| inccm | 0,50 | 0,36 | 0,65 | 6,80 | 6,95 | 6,94 |
| igpdi | 0,53 | 1,21 | 3,74 | 3,46 | ||
| ipadi | 0,41 | 1,24 | 1,67 | 1 | ||
| ipcdi | 0,97 | 1,41 | 7,99 | 8,59 | ||
| inccdi | 0,50 | 0,36 | 6,80 | 6,95 | ||
| ipaagro | 1,12 | 2,10 | 6,17 | 2,68 | ||
| ipaind | 0,13 | 0,90 | 0,01 | 0,34 | ||
| ipca15 | 1,33 | 1,24 | 1,07 | 7,36 | 7,90 | 8,22 |
| ipca | 1,22 | 1,32 | 7,70 | 8,13 | ||
Pronto! Aí está uma tabelinha com as últimas observações de vários índices de inflação no país. Ela contém a variação mensal e a anual dos últimos dados disponíveis desses índices. Observe o leitor que o último dado disponível do IPCA-15 é de abril, que mostra uma inflação acumulada em 12 meses de 8,22%. Alternativamente, você pode colocar mais meses utilizando a função tail com um n maior. Mostrados os dados, vamos agora ver alguns gráficos selecionados das séries que geramos. Mostro uma sequência de código e gráfico abaixo.
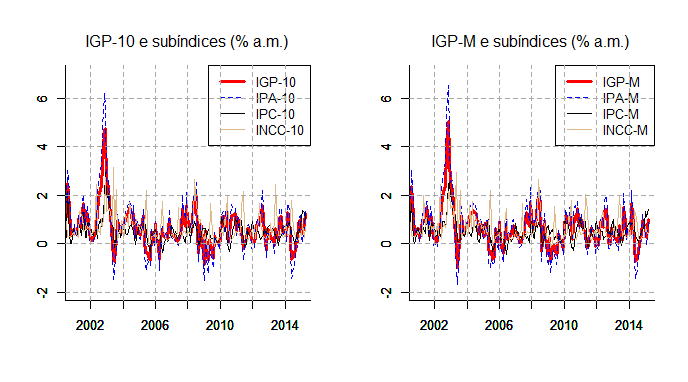
################# IGP-10 e IGP-M [e subíndices] ##################
par()
op <- par()
lay <- layout(matrix(c(1,1,2,2), ncol=2, byrow=F))
layout.show(lay)
plot(igp10mensal, main='' ,
sub='',
col="red", lty=1, lwd=3, xlab='',ylab='',bty='l',
ylim=c(-2,7), xlim=c(2001,2015))
par(new=T)
plot(ipa10mensal, main='' ,
sub='',
col="blue", lty=2, lwd=1, xlab='',ylab='',bty='l',
ylim=c(-2,7), xlim=c(2001,2015))
par(new=T)
plot(ipc10mensal, main='' ,
sub='',
col="black", lty=1, lwd=1, xlab='',ylab='',bty='l',
ylim=c(-2,7), xlim=c(2001,2015))
par(new=T)
plot(incc10mensal, main='' ,
sub='',
col="burlywood", lty=1, lwd=1, xlab='',ylab='',bty='l',
ylim=c(-2,7), xlim=c(2001,2015))
legend('topright', col=c('red','blue','black',
'burlywood'), lty=c(1,2,1,1), lwd=c(3,1,1,1),
legend=c('IGP-10', 'IPA-10','IPC-10','INCC-10'))
grid(lty=2, lwd=1, col='darkgrey')
mtext('IGP-10 e subíndices (% a.m.)',side=3,line=1, col='black',
font=1)
plot(igpmmensal, main='' ,
sub='',
col="red", lty=1, lwd=3, xlab='',ylab='',bty='l',
ylim=c(-2,7), xlim=c(2001,2015))
par(new=T)
plot(ipammensal, main='' ,
sub='',
col="blue", lty=2, lwd=1, xlab='',ylab='',bty='l',
ylim=c(-2,7), xlim=c(2001,2015))
par(new=T)
plot(ipcmmensal, main='' ,
sub='',
col="black", lty=1, lwd=1, xlab='',ylab='',bty='l',
ylim=c(-2,7), xlim=c(2001,2015))
par(new=T)
plot(inccmmensal, main='' ,
sub='',
col="burlywood", lty=1, lwd=1, xlab='',ylab='',bty='l',
ylim=c(-2,7), xlim=c(2001,2015))
legend('topright', col=c('red','blue','black',
'burlywood'), lty=c(1,2,1,1), lwd=c(3,1,1,1),
legend=c('IGP-M', 'IPA-M','IPC-M','INCC-M'))
grid(lty=2, lwd=1, col='darkgrey')
mtext('IGP-M e subíndices (% a.m.)',side=3,line=1, col='black',
font=1)
par(op)
Esse gráfico coloca as variações mensais do IGP-10 e do IGP-M, bem como seus determinantes (IPA, IPC e INCC) em evidência. Observe que o comportamento dos mesmos é bastante parecido. Isso pode ser mais nitidamente visto com o gráfico seguinte, que acumula os dois e o IGP-DI em 12 meses.
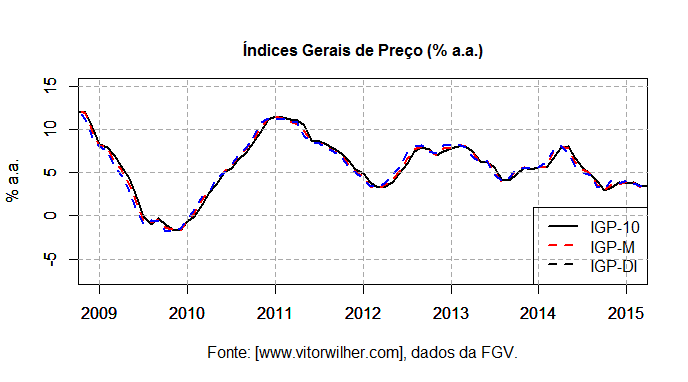
## Análise Gráfica dos IGPs
par()
opar <- par()
plot(igp10anual, xlab='', ylab='% a.a.',xlim=c(2009,2015),
ylim=c(-7,15), lty=1, lwd=2, col='black')
par(new=T)
plot(igpmanual, xlab='', ylab='% a.a.',xlim=c(2009,2015),
ylim=c(-7,15), lty=2, lwd=2, col='red')
par(new=T)
plot(igpdianual, xlab='', ylab='% a.a.',xlim=c(2009,2015),
ylim=c(-7,15), lty=2, lwd=2, col='blue')
legend('bottomright', col=c('black', 'red','black'),
lty=c(1,2,2), lwd=c(2,2,2),
legend=c('IGP-10', 'IGP-M', 'IGP-DI'))
grid(lty=2, lwd=1, col='darkgrey')
mtext('Índices Gerais de Preço (% a.a.)',side=3,line=1, col='black',
font=2)
mtext('Fonte: [analisemacro.com.br], dados da FGV.',
side=1,line=3)
par(opar)
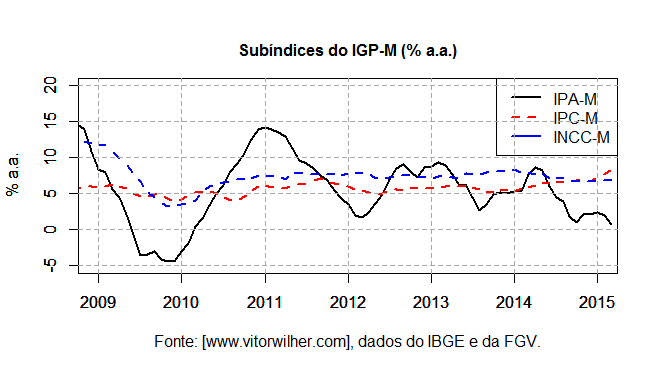
Os três IGPs mostram uma queda seguida de estabilidade no período recente. Para ver qual dos três componentes do IGP está causando esse comportamento, podemos plotar um gráfico com os mesmos. É o que faço abaixo [o código é similar ao colocado acima] com a série M dos subíndices. É possível observar no gráfico que enquanto o IPC e o INCC se mantém razoavelmente constantes, o IPA mostra o comportamento captado pelo índice cheio (IGP). Em outros termos, os índices gerais mostram o comportamento predominantemente observado no atacado.
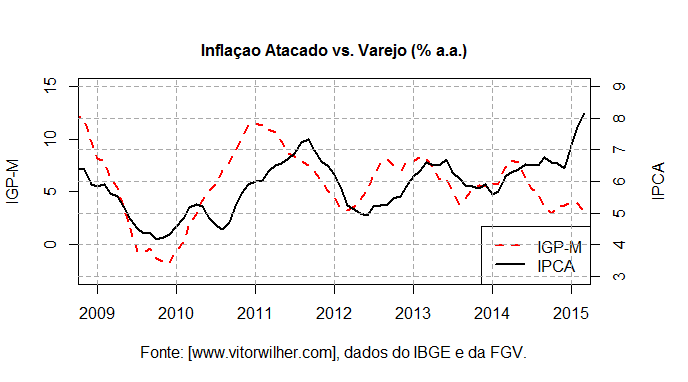
Essa é, a propósito, uma das grandes diferenças entre os IGPs e o IPCA. O IPA, índice de preços no atacado, é responsável por 60% dos IGPs. Enquanto isso, o IPCA reflete os preços que o consumidor com renda de 1 a 40 salários-mínimos enfrenta no dia a dia. Pensando nisso, podemos montar um gráfico com um dos IGPs e com o IPCA, para ver a diferença entre ambos no período recente e dar uma luz de como devemos entender a inflação. O código e o gráfico seguem abaixo.
## IPCA vs. IGP-M
par()
opar <- par()
par(mar=c(5,4,4,5)+.1)
plot(igpmanual,type='l',col='red', lty=2, lwd=2,
xlab='', ylab='IGP-M', ylim=c(-3,15),
xlim=c(2009,2015), main='')
par(new=T)
plot(ipcaanual, type='l', col='black',
xaxt='n',yaxt='n', lty=1, lwd=2,
xlab='', ylab='', xlim=c(2009,2015), ylim=c(3,9))
axis(4)
mtext('IPCA',side=4,line=3)
legend('bottomright', col=c('red','black'), lty=c(2,1), lwd=2,
legend=c('IGP-M', 'IPCA'))
grid(lty=2, lwd=1, col='darkgrey')
mtext('Inflaçao Atacado vs. Varejo (% a.a.)',side=3,line=1, col='black',
font=2)
mtext('Fonte: [analisemacro.com.br], dados do IBGE e da FGV.',
side=1,line=3)
par(opar)
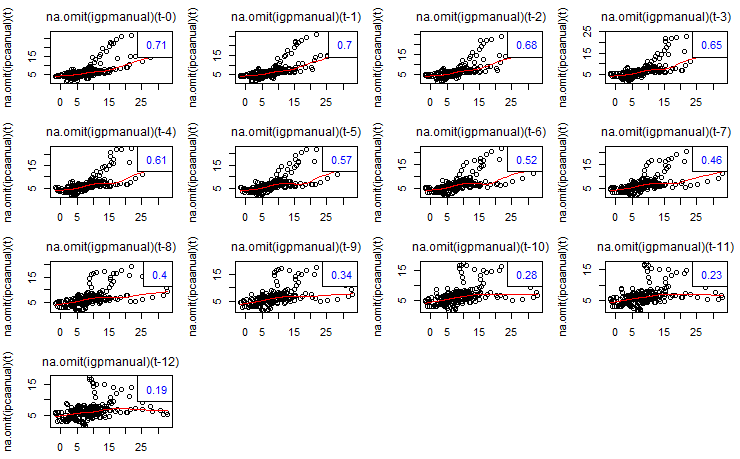
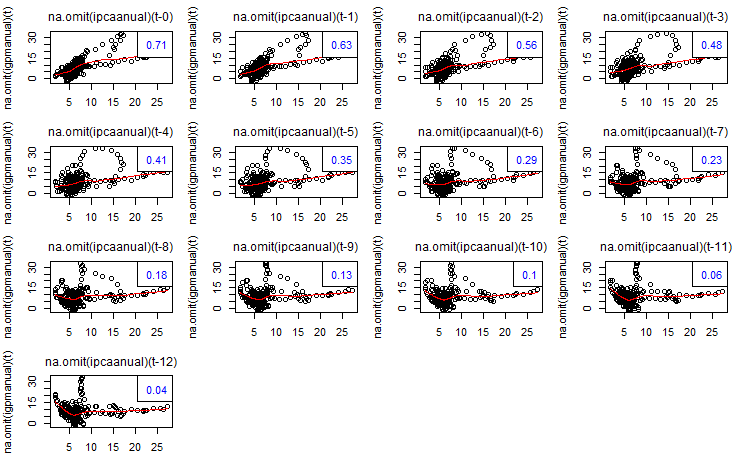
Pois é, leitor. Ao longo do tempo, o IGP tende a ter o mesmo comportamento do IPCA e, em certo grau, um antecipa o outro, dado o componente de "inflação no atacado" contido no primeiro [isso é algo interessante que você poderia testar, não?]. Podemos, inclusive, ver essa correlação cruzada de forma gráfica no R com a função lag2.plot do pacote astsa (dica do Claudio Shikida), como colocado abaixo. No período recente, entretanto, enquanto o IGP-M mostra um comportamento de no mínimo estabilidade, o IPCA deu um "salto" nos últimos meses. Ademais, mesmo antes desse "salto" no IPCA, a "boca de jacaré" entre IPCA e IGP-M já era pronunciada. Em outros termos, enquanto os IGPs registram a desaceleração na economia, o IPCA não só resistiu em um patamar mais elevado, como se acelerou nos últimos meses.
Para compreender os motivos pelos quais o IPCA mostra um comportamento dissonante em relação aos índices gerais, devemos olhar mais detidamente para ele. É o que faremos no próximo post dessa série! Espero que tenham gostado desse primeiro exemplo de exploração de dados, usando a inflação e o R. 🙂
# Correlação cruzada entre IGP-M e IPCA, ambos acumulados em 12 meses lag2.plot(na.omit(igpmanual),na.omit(ipcaanual),12,corr=TRUE) lag2.plot(na.omit(ipcaanual),na.omit(igpmanual),12,corr=TRUE)
_______________________________________
Gostou do post? Quer aprender a fazer o mesmo? Dê uma olhada no nosso curso de Introdução ao R com aplicações em Análise de Conjuntura. Faça no Rio de Janeiro ou leve para sua empresa ou universidade!
________________________________________