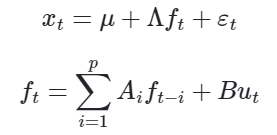O Produto Interno Bruto (PIB) é a soma de todos os bens e serviços finais produzidos por um país, estado ou cidade, em um determinado período no tempo. É um indicador que ajuda a compreender a dinâmica de crescimento da economia como um todo, constituindo uma variável macroeconômica relevante para o governo, para a política monetária e para a população de forma geral.
O PIB é resultado de uma série de cálculos contábeis e, em resumo, existem três óticas para calcular o PIB:
- Oferta (produto): PIB é igual ao valor bruto da produção, a preços básicos, menos o consumo intermediário, a preços de consumidor, mais os impostos, líquidos de subsídios, sobre produtos;
- Demanda (despesa): PIB é igual a despesa de consumo das famílias, mais o consumo do governo, mais o consumo das instituições sem fins de lucro a serviço das famílias (consumo final), mais a formação bruta de capital fixo, mais a variação de estoques, mais as exportações de bens e serviços, menos as importações de bens e serviços;
- Renda: PIB é igual à remuneração dos empregados, mais o total dos impostos, líquidos de subsídios, sobre a produção e a importação, mais o rendimento misto bruto, mais o excedente operacional bruto.
Os dados do PIB são divulgados trimestralmente pelo IBGE nas Contas Nacionais Trimestrais. Nesse sistema são disponibilizados os valores correntes (R$) e índice de volume (base: média de 1995 = 100) para o PIB e seus componentes.
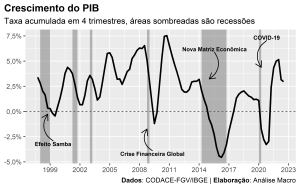
A evolução do PIB brasileiro no período recente pode ser conferida no gráfico abaixo:
A economia brasileira já passou por diversas crises nas últimas décadas, internas e externas, o que faz com que sua taxa de crescimento seja um tanto quando volátil. A média de crescimento, medida pelo PIB, desde o final dos anos 90 gira em torno de 2,16%, em termos anuais.
Pela complexidade de cômputo e pela sensibilidade a crises e choques adversos, é razoável pensar que produzir previsões para o PIB é uma tarefa difícil e não muito glamourosa para profissionais que trabalham com previsão. De fato, é um desafio e neste exercício vamos explorar algumas abordagens disponíveis, desde as mais simples até as mais complexas, com o objetivo de comparar opções em termos de acurácia.
Abordagem 1: modelos univariados
A abordagem mais simples possível é modelar o PIB com o uso de modelos univariados de séries temporais, como o modelo ARIMA que é usado pelo próprio IBGE para o processo de ajuste sazonal da série do PIB.
Por sua simplicidade, não podemos esperar resultados muito interessantes destes modelos, dado que eles exploram, basicamente, os valores passados da série temporal para previsão de valores futuros. Na economia nem sempre o passado é útil para explicar ou prever o futuro. A forma geral destes modelos é essa:
Aqui y′ é a série temporal estacionária (em nível ou nas diferenças), c é uma constante (intercepto) do modelo, ε é o erro defasado e os demais termos são parâmetros a serem estimados. Na prática utiliza-se a metodologia de Box & Jenkins e para mais detalhes veja Hyndman e Athanasopoulos (2021).
Abordagem 2: modelos hierárquicos
A série do PIB é resultado da soma de alguns componentes, a depender da ótica de cálculo empregada. Explorando essa característica, existe uma literatura que explora técnicas envolvendo modelos de previsão hierárquicos de maneira a, por exemplo, desagregar a série “total” em componentes, modelar e produzir previsões para estes componentes e, por fim, agregar as previsões individuais para obter a previsão da série “total”.
De modo geral, podemos representar essa técnica, aplicada ao PIB pela ótica da oferta, como:
Ou seja, para qualquer observação no tempo t para a série PIB, as observações no nível inferior da hierarquia da série (neste caso, os componentes de valor adicionado e impostos líquidos) serão agregadas para formar as observações da série acima.
Existem várias abordagens para gerar previsões hierárquicas com séries temporais, a mais comum e intuitiva é a bottom-up (de baixo para cima), descrita acima, onde primeiro geramos as previsões para cada série no nível inferior e, em seguida, somamos os pontos de previsão para obter previsões da série acima.
Por outro lado, a abordagem top-down (de cima para baixo) envolve primeiro a geração de previsões para a série agregada e, em seguida, desagregá-la na hierarquia utilizando proporções (geralmente baseadas na série histórica).
Ainda existem outras abordagens como a do Minimum Trace e suas variantes, sendo que cada uma tem seus prós e contras. Para um exemplo veja este artigo e para mais detalhes veja Hyndman e Athanasopoulos (2021).
Em relação ao termo de impostos líquidos, escolhemos deixá-lo fora da modelagem e assumimos uma regra de cerca de 16,5% do valor adicionado (participação média história de imp. liq. em relação ao VA) como lei de movimento para o mesmo no futuro, de forma similar ao que o colega economista Felipe Camargo faz. Ao final, o valor calculado é somado ao valor adicionado para formar o PIB.
Abordagem 3: modelos de nowcasting
Nowcasting é uma abordagem moderna para monitorar as condições econômicas em tempo real. Diferentemente das técnicas de previsão tradicionais, nesta abordagem o interesse é em prever os indicadores durante o período de referência dos mesmos, ou logo após eles.
Por exemplo, o PIB é divulgado para os trimestres de cada ano — esse é o período de referência da série —, no entanto, a publicação dos dados só é realizada após a compilação dos dados e cálculos internos pelo IBGE, o que costuma acontecer dois meses após o período de referência. Neste caso, a abordagem de nowcasting seria empregada durante o período de referência ou até antes da data de divulgação dos dados.
O método mais utilizado por trás das previsões de um nowcasting é o modelo de fator dinâmico, que condensa a informação de numerosas séries de dados em um pequeno número de fatores. A representação em espaço de estado do modelo de fator dinâmico formaliza como os mercados leem os dados econômicos em tempo real. O filtro de Kalman gera projeções para todas as séries de dados e estimativas para cada lançamento. Quando há o anúncio de novos dados, há uma alteração no modelo, chamada de “notícia”.
Formalmente, o modelo de fator dinâmico é representado com duas equações:
Na primeira equação, x representa séries temporais observáveis que são expressadas como uma função de um intercepto μ, de r fatores comuns não observáveis f e de um termo de erro aleatório ε. As variáveis observáveis x são carregadas para fatores comuns não observáveis via Λ. Na segunda equação, é imposto uma estrutura de um processo VAR(p) para os fatores f, onde A são os coeficientes autorregressivos e u é um termo de erro aleatório. Para mais detalhes veja De Valk et al. (2019).
Abordagem 4: técnicas de aprendizagem de máquina
Em um contexto crescente de abundância de dados e de recursos computacionais, as técnicas de aprendizagem de máquina têm sido cada vez mais utilizadas no contexto de previsão de variáveis macroeconômicas. Existem diversos métodos disponíveis e a literatura especializada está em constante evolução.
Para o propósito deste exercício selecionamos o algoritmo XGBoost para testar. É um algoritmo de aprendizagem de máquina que constrói um modelo de previsão com base em uma combinação de vários modelos de previsão considerados “fracos”, geralmente usando árvores de decisão (decision trees) e aumento de gradiente (gradient boosting). Isso significa que o algoritmo utiliza um método de otimização (método do gradiente) para minimizar uma função perda (como o RMSE) a cada modelo fraco adicional. Saiba mais na Wikipédia e em Chen e Guestrin (2016).
Estratégia de previsão
Propomos uma estratégia como uma forma sistemática de acompanhamento dos dados, previsão e avaliação de modelos para o PIB do Brasil.
A principal motivação de ter uma estratégia bem definida é por conta do “problema de borda irregular” ou, no inglês, ragged edge problem (Wallis, 1986). Esse problema acontece quando há diferenças nos atrasos de publicação entre as variáveis de um modelo, resultando em um conjunto incompleto de dados para o período mais recente. Existem algumas alternativas para contornar o problema, mas, em geral, é empregado um método de imputação de dados.
Para o propósito deste exercício de previsão a ideia é produzir previsões utilizando toda a informação disponível sempre um mês antes da divulgação do próximo dado do PIB para qualquer período de referência, o que totaliza 4 previsões por ano. Um mês após gerar previsões, ℎ períodos à frente, o PIB do último período de referência é divulgado e então é hora de avaliar a acurácia das últimas previsões dos modelos. Entre período de avaliação de acurácia dos modelos e a próxima produção de previsões para o PIB, os dados de maior frequência devem ser acompanhados e ajustes dos modelos podem ser feitos.
Um resumo do problema da borda irregular e um desenho de estratégia de previsão aplicada ao PIB é exposto abaixo:
Dados
Resumimos na tabela abaixo as variáveis utilizadas nos modelos para previsão do PIB. Utilizou-se somente dados de fontes públicas e de acesso gratuito, visando a possibilidade de replicação por interessados.
| Variável | Descrição | Unidade de Medida | Fonte | Abordagem |
|---|---|---|---|---|
| PIB | Brasil, a preços de mercado, valores encadeados a preços de 1995 | R$ (milhões) | CNT/IBGE | 1, 2, 3, 4 |
| Valor adicionado da Agropecuária | Brasil, ótica da oferta do PIB, valores encadeados a preços de 1995 | R$ (milhões) | CNT/IBGE | 2 |
| Valor adicionado da Indústria | Brasil, ótica da oferta do PIB, valores encadeados a preços de 1996 | R$ (milhões) | CNT/IBGE | 2 |
| Valor adicionado de Serviços | Brasil, ótica da oferta do PIB, valores encadeados a preços de 1997 | R$ (milhões) | CNT/IBGE | 2 |
| Impostos líquidos sobre produtos | Brasil, ótica da oferta do PIB, valores encadeados a preços de 1998 | R$ (milhões) | CNT/IBGE | 2 |
| Renda real | Rendimento real médio de todos os trabalhos habituais mensais | R$ do penúltimo mês da série | PNADC/IBGE | 3, 4 |
| Força de trabalho | Pessoas na força de trabalho | Pessoa (mil) | PNADC/IBGE | 3, 4 |
| Taxa de desocupação | Percentual de pessoas desocupadas em relação às pessoas na força de trabalho | % | PNADC/IBGE | 3, 4 |
| Número de empregados | Saldo do antigo e novo Caged | Pessoa | ME | 3, 4 |
| Ibovespa | Índice de ações, fechamento | % a.m. | Anbima | 3, 4 |
| ETTJ | Taxa de juros pré fixada, LTN, 12 meses | % a.a. | Anbima | 3, 4 |
| Exportações | Balança comercial, BPM6 | US$ (milhões) | BCB | 3, 4 |
| Importações | Balança comercial, BPM6 | US$ (milhões) | BCB | 3, 4 |
| M1 | Meio de pagamento restrito, média | R$ (milhões) | BCB | 3, 4 |
| Taxa de câmbio | R$ / US$, nominal, comercial, venda, média | R$ | BCB | 3, 4 |
| IBC-Br | Índice real de atividade econômica do Banco Central (2002=100) | Índice | BCB | 3, 4 |
| Produção industrial | Produção Física Industrial, Indústria geral, PIM-PF | Var. % m/m-1 | IBGE | 3, 4 |
| Produção de bens de consumo | Produção Física Industrial, Bens de consumo, PIM-PF | Var. % m/m-1 | IBGE | 3, 4 |
| Produção de insumos de construção | Produção Física Industrial, Insumos típicos da construção civil, PIM-PF | Var. % m/m-1 | IBGE | 3, 4 |
| Produção agrícola | Levantamento Sistemático da Produção Agrícola, Milho (1ª e 2ª Safra) e Soja | Produção (Toneladas) | IBGE | 3, 4 |
| Custo médio m² | Custo médio m², SINAPI | Var. % 12 meses | IBGE | 3, 4 |
| Índice de serviços | Pesquisa Mensal de Serviços, Índice de receita nominal de serviços | Var. % m/m-1 | IBGE | 3, 4 |
| Índice de inflação | IPCA, dessazonalizado | Var. % m/m-1 | IBGE | 3, 4 |
| ICEA | Índice de Condições Econômicas Atuais | Índice | Fecomercio | 3, 4 |
| IVG-R | Índice de Valores de Garantia de Imóveis Residenciais Financiados | Índice | BCB | 3, 4 |
| Vendas de autoveículos | Total | Unidades | Anfavea | 3, 4 |
| IMC | Indicador de Movimento do Comércio a Prazo | - | ACSP | 3, 4 |
| Índice de comércio | Pesquisa Mensal de Comércio, Índice de volume de vendas no comércio varejista (2014=100) | Índice | IBGE | 3, 4 |
| Taxa de câmbio real | Real Broad Effective Exchange Rate for Brazil (2020=100) | Índice | BIS | 3, 4 |
| Condições econômicas dos EUA | Coincident Economic Activity Index for the United States (2007=100) | Índice | FED Philadelphia | 3, 4 |
| Taxa de juros interbancária | Immediate Rates, less than 24 hours: call money/interbank rate for Brazil | % | MEI/OCDE | 3, 4 |
| Confiança da indústria composto | Business Tendency Surveys for Manufacturing, confidence indicators, composite indicators (normal=100) | Índice normalizado | MEI/OCDE | 3, 4 |
| Indicador de expectativa de exportação | Business Tendency Surveys for Manufacturing, export order books or demand, level | % | MEI/OCDE | 3, 4 |
| Expectativa da UCI | Business Tendency Surveys for Manufacturing, capacity utilisation | % | MEI/OCDE | 3, 4 |
| Expectativa de emprego | Business tendency surveys (retail trade), employment, future tendency | % | MEI/OCDE | 3, 4 |
| Confiança do consumidor composto | Consumer Opinion Surveys, confidence indicators, composite indicators (normal=100) | Índice normalizado | MEI/OCDE | 3, 4 |
| Buscas por “seguro desemprego” | Termo de pesquisa no Google Search, medida de interesse, Google Trends | Índice | 3, 4 | |
| Índice de mercados emergentes | NASDAQ Emerging Markets Index, NQEM | - | NASDAQ | 3, 4 |
A série de interesse para este exercício de previsão é: variação do PIB em relação ao mesmo período do ano anterior, sem ajuste sazonal. Essa é a mesma medida coletada pelo Banco Central em seu sistema de expectativas, o que possibilita comparar as previsões do exercício com as previsões de agentes de mercado.
Transformações e seleções nas séries temporais são aplicadas conforme a necessidade de cada abordagem.
Resultados
Aproximando os modelos aos dados expostos, fizemos um exercício de previsão dividindo a amostra de dados em duas: uma amostra de teste, constituindo as últimas 4 observações (um ano de dados), usada para gerar previsões e comparar os resultados com os dados observados; e uma amostra de treino, usada para estimar os parâmetros dos modelos.
Dentre as abordagens expostas a única que necessita de cenários é a abordagem 4. Optamos por adotar como cenário a hipótese de valores constantes do último dado observado para as variáveis exógenas por todo o período da amostra de teste. É o cenário mais ingênuo possível, sem nenhuma leitura das condições econômicas contemporâneas, mas ao mesmo tempo não enviesa os resultados ao adicionar informação já conhecida de antemão para produzir previsões nesta abordagem. Isso é uma escolha arbitrária, não há “regras”.
Abaixo estão as previsões geradas por cada abordagem no período da amostra de teste (previsões pseudo “fora da amostra”):
| Período | PIB | ARIMA | ARIMA Agregado | ARIMA Bottom Up | ARIMA Min-Trace | ARIMA Top Down | DFM | XGBoost |
|---|---|---|---|---|---|---|---|---|
| 2021 Q4 | 2.132304 | 2.1404548 | 0.6090033 | 0.8661318 | 0.6732854 | 0.6090033 | 5.5855082 | 4.63089 |
| 2022 Q1 | 2.426989 | 1.3244310 | 2.0949469 | 2.9137801 | 2.2996552 | 2.0949469 | 2.7913566 | 4.63089 |
| 2022 Q2 | 3.685227 | -2.6324123 | 0.4685606 | 0.7913568 | 0.5492596 | 0.4685606 | 1.5300012 | 4.63089 |
| 2022 Q3 | 3.579165 | 0.8813207 | 0.8673031 | 0.9584401 | 0.8900873 | 0.8673031 | 0.9494037 | 4.63089 |
O período da amostra de teste é um tanto quanto desafiador para qualquer modelo de previsão de variáveis macroeconômicas, dado os efeitos de choques e pandemia que ainda se refletem na unidade de medida da variável de interesse (var. % em t contra o mesmo período do ano anterior). As previsões dos modelos são bastante heterogêneas, mesmo dentro de uma única abordagem, e os modelos “sofrem” para entender a dinâmica do PIB no período.
Para comparar os modelos em termos de acurácia, calculamos o erro de previsão e geramos as métricas tradicionais expostas na tabela abaixo:
| Abordagem | Modelo | Erro Médio | Erro Quadrático Médio | Raiz do Erro Quadrático Médio | Erro Médio Absoluto | Erro Percentual Médio |
|---|---|---|---|---|---|---|
| Técnicas de ML | XGBoost | -1.6749688 | 3.275129 | 1.809732 | 1.674969 | -65.75784 |
| Modelos Hierárquicos | ARIMA Bottom Up | 1.5734939 | 4.270710 | 2.066570 | 1.816890 | 47.76774 |
| Modelos Hierárquicos | ARIMA Min-Trace | 1.8528492 | 4.802594 | 2.191482 | 1.852849 | 58.47453 |
| Modelos Hierárquicos | ARIMA Agregado | 1.9459677 | 5.032958 | 2.243426 | 1.945968 | 62.04346 |
| Modelos Hierárquicos | ARIMA Top Down | 1.9459677 | 5.032958 | 2.243426 | 1.945968 | 62.04346 |
| Modelos de Nowcasting | DFM | 0.2418537 | 5.904506 | 2.429919 | 2.150640 | -11.25081 |
| Modelos Univariados | ARIMA | 2.5274726 | 12.101657 | 3.478744 | 2.531548 | 72.96366 |
Os resultados da comparação de acurácia dos modelos são interessantes e são inclinados para abordagens de previsão mais complexas e com maior dimensionalidade de dados, com destaque para o modelo XGBoost e para as abordagens hierárquicas. O PIB é uma variável estimada a partir de uma infinidade de dados de uma infinidade de fontes, portanto esse resultado não deveria surpreender. O resultado para o modelo de nowcasting é esperado, dado que é uma abordagem desenhada para o curtíssimo prazo, portanto a comparação do mesmo com os demais pode ser injusta. A tabela está ordenada pela métrica da Raiz do Erro Quadrático Médio.
Alguns dos próximos passos desse exercício de previsão são destacados abaixo:
- Confirmar se estes resultados se generalizam para outras amostras, ou seja, implementar alguma validação cruzada;
- Analisar os resultados por horizonte preditivo, dado que, conforme observado, é esperado que alguns modelos performem melhor em determinados horizontes;
- Comparar a acurácia com o benchmark de mercado, ou seja, as previsões do Focus/BCB.
Para implementar este exercício de previsão, passando pelos procedimentos de coleta, tratamento, modelagem/estatística e visualização de dados, utilizamos a linguagem R. Para reprodução de resultados utilizamos a semente 1984.
Saiba mais
Códigos de reprodução em R deste exercício estão disponíveis para membros do Clube AM da Análise Macro.
Para se aprofundar no assunto confira os cursos aplicados de R e Python da Análise Macro:
- Trilha de Macroeconomia Aplicada: https://conteudosam.com.br/pacotes/macroeconomia-aplicada/
- Trilha de Machine Learning e Econometria: https://conteudosam.com.br/pacotes/econometria-e-machine-learning/
- Modelos Preditivos: https://analisemacro.com.br/curso/modelos-preditivos-de-machine-learning/
- Econometria: https://analisemacro.com.br/cursos/econometria/introducao-a-econometria/
- Análise de Séries Temporais: https://conteudosam.com.br/cursos/analise-de-series-temporais/
Referências
Chen, T., & Guestrin, C. (2016). Xgboost: A scalable tree boosting system. In 22nd SIGKDD Conference on Knowledge Discovery and Data Mining.
De Valk, S., de Mattos, D., & Ferreira, P. (2019). Nowcasting: An R package for predicting economic variables using dynamic factor models. The R Journal, 11(1), 230-244.
Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2023-02-27.
Wallis, K. F. (1986). Forecasting with an econometric model: The ‘ragged edge’ problem. Journal of Forecasting, 5(1), 1-13.