Quem trabalha com modelagem e previsão provavelmente já teve que construir modelos baseados em vetores autorregressivos. Nessa Dicas de R - disponível toda quarta-feira aqui no blog da AM -vamos mostrar como é possível implementar esse tipo de modelo no R e utilizá-lo para fins de previsão. Essa aula, inclusive, faz parte do nosso novíssimo Curso de Previsão Macroeconométrica usando o R.
Em análises de séries temporais, é bastante comum considerar simultaneamente duas ou mais séries. Por exemplo, o nível de ociosidade da economia certamente tem influência sobre a taxa de crescimento dos preços, assim como um aumento da taxa de juros tem relação com a taxa de desemprego. Ademais, pode ser necessário em algumas ocasiões avaliar o quanto um choque em afeta
. Essas questões, bastante pertinentes no dia a dia, são tratadas dentro do que chamamos de análise multivariada de séries temporais. São objetivos básicos da análise multivariada de séries temporais:
- Estudar as relações dinâmicas entre séries diversas;
- Melhorar as previsões sobre uma variável específica.
Seja um vetor de dimensão
que contém séries temporais observadas em um período de tempo comum. Por exemplo,
é o PIB trimestral brasileiro e
é a taxa de desemprego também trimestral. Acaso, estudemos
e
conjuntamente poderemos verificar a dependência contenporânea e passada que existe entre essas duas variáveis. Poderemos verificar o quanto um choque no PIB afeta a taxa de desemprego e quanto tempo isso tende a durar. Analogamente, podemos estar interessados na relação entre a taxa de desemprego e a inflação.
desemprego = Quandl('BCB/24369', start_date='2012-03-01',
end_date='2018-12-01', order='asc', type='ts')
inflacao = Quandl('BCB/13522', start_date='2013-03-01',
end_date='2019-12-01', order='asc', type='ts')
data = data.frame(desemprego, inflacao)
A correlação entre as variáveis é -0,81, bastante elevada, mas isso, claro, não é o bastante para identificarmos a natureza da relação entre elas. Algumas questões devem ser levadas em consideração. Em primeiro lugar, para uma análise econométrica, precisamos definir se as séries são estacionárias. Essa primeira (grande) questão definirá o tipo de análise que faremos entre elas. Vamos supor que elas sejam estacionárias. Podemos, nesse caso, estimar um \textbf{Vetor Autoregressivo} de primeira ordem, de modo que:
(1)
O VAR(1) vai descrever a evolução dinâmica da interação entre a inflação e desemprego. Uma vez estimado esse modelo, poderemos nos perguntar se existe causalidade nessa relação, isto é, se inflação de fato ajuda a prever o desemprego, se o contrário ocorre ou se há uma simultaneidade. Nesse último caso, dizemos que existe uma causalidade bidirecional.
Ademais, esse tipo de análise também irá nos permitir estimar funções de impulso-resposta, onde analisamos a resposta a impulsos em uma das variáveis. Por exemplo, um choque no desemprego tem qual efeito sobre a inflação? E o caso contrário? Uma análise como essa pode ser muito interessante para avaliar a relação que existe entre duas ou mais variáveis, não é mesmo?
Um dos pressupostos, entretanto, do modelo acima é que as variáveis sejam estacionárias, no sentido que discutimos anteriormente. Isso significa que se essa hipótese for violada, teremos que partir para outro tipo de análise. No nosso Curso de Previsão Macroeconométrica usando o R, discutiremos a existência de cointegração entre duas ou mais variáveis, isto é, para o caso em que lidamos com séries não estacionárias, pode ser o caso de nos perguntarmos se existe uma relação entre de longo-prazo entre elas. Para o exemplo acima, se as séries não forem estacionárias, como de fato aparentam não ser, as mesmas podem estar relacionadas ao longo do tempo. Se for esse o caso, dizemos que as séries possuem uma tendência comum, o que nos permite avaliar a relação entre elas ao longo do tempo.
Para além disso, vamos agora ilustrar a aplicação de um modelo VAR a dados reais brasileiros. Estamos, por suposto, interessados em construir um modelo VAR que seja utilizado para fins de previsão da inflação mensal medida pelo IPCA. Para isso, vamos começar, como de praxe, carregando alguns pacotes.
### Pacotes library(ggplot2) library(forecast) library(mFilter) library(BETS) library(vars) library(scales) library(gridExtra) library(stargazer)
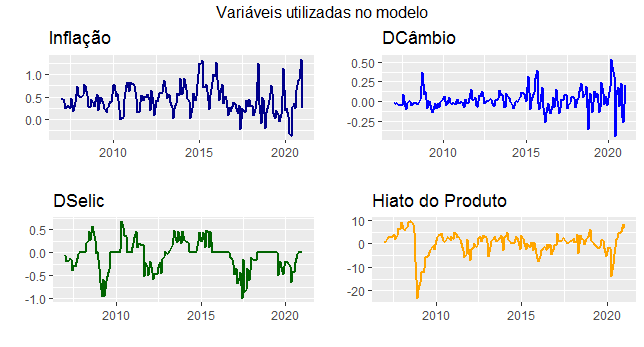
Os dados que precisaremos são coletados com uso do pacote \texttt{BETS} abaixo. Pegamos as séries de inflação, taxa Selic, taxa de câmbio e a produção industrial. Ademais, já tratamos as séries, preparando-as para o modelo VAR.
### Coletar os dados
inflacao <- BETSget(433)
selic <- BETSget(4189)
cambio <- BETSget(3697)
industria <- BETSget(21940)
# Transformações
dselic <- diff(selic)
dcambio <- diff(cambio)
# Criar e projetar hiato t+1
hp <- hpfilter(industria, freq=14400, type='lambda')
hiato <- ts(hp$cycle, start=start(industria), freq=12)
hiatof <- forecast(auto.arima(hiato, max.p=4, max.q=4,
seasonal = F), h=1, level=40)$mean
hiato <- ts(c(hiato, hiatof), start=start(industria), freq=12)
# Criar dummies sazonais
dummies <- window(ts(seasonaldummy(inflacao),
start=start(inflacao), freq=12), start=c(2007,01))
# Juntar séries
data <- window(ts.intersect(inflacao, dselic, dcambio, hiato),
start=c(2007,01))
colnames(data) <- c('inflacao', 'dselic', 'dcambio', 'hiato')
Um gráfico com as séries que utilizaremos é colocado abaixo.
Coletados e tratados os dados, o modelo VAR é então estimado com o código abaixo.
lag <- VARselect(data, lag.max=12, type='trend', season = 12) var <- VAR(data, min(lag$selection), type='both', exogen = dummies)
Com o modelo em mãos, podemos gerar uma previsão como abaixo.
# Previsão h <- 7 fvar <- stats::predict(var, n.ahead=h, ci=.4, dumvar=head(dummies,h)) fvar$fcst$inflacao
O output da previsão pode ser visto abaixo.
| fcst | lower | upper | CI | |
|---|---|---|---|---|
| 1 | 0.38 | 0.25 | 0.51 | 0.13 |
| 2 | 0.45 | 0.30 | 0.59 | 0.15 |
| 3 | 0.41 | 0.26 | 0.56 | 0.15 |
| 4 | 0.40 | 0.25 | 0.55 | 0.15 |
| 5 | 0.36 | 0.20 | 0.51 | 0.15 |
| 6 | 0.30 | 0.14 | 0.45 | 0.15 |
| 7 | 0.24 | 0.09 | 0.39 | 0.15 |
Esse tipo de modelagem é bastante utilizado entre profissionais que precisam de previsões acuradas no curto prazo para diversos tipos de variáveis. Ela é vista em detalhes nos nossos Cursos avançados de Macro Aplicada e de Análise de Séries Temporais.
____________________