Modelos ARIMA na abordagem bayesiana

A boa e velha econometria nos proporciona métodos que são ótimos para relacionar variáveis e construir previsões, sendo quase sempre o primeiro ponto de partida para praticantes, além de ser a base de grande parte dos modelos "famosos" da atualidade. Como exemplo, em problemas de previsão de séries temporais a família de modelos ARIMA, popularizada por Box e Jenkins (1970), costuma ser a primeira opção que vem à mente.

Uma das suposições destes modelos é a de que os erros — ou seja, a diferença entre o que é observado e o que é estimado — seguem uma distribuição normal, o que no mundo real nem sempre é factível com os dados que temos em mãos. E então, o que fazer nessa situação? Devemos descartar os modelos ARIMA e usar outra classe de modelos? Ou devemos descartar os dados, pois, claramente, "eles não se encaixam no modelo"?

Bom, nada disso! Em primeiro lugar, eu afirmaria que os modelos ARIMA ainda podem ser úteis. Em segundo lugar, neste exercício apresentarei uma visão diferente no que se refere ao método de estimação do modelo, trazendo uma breve introdução à abordagem bayesiana. Por fim, exemplificarei com um modelo ARIMA simples as diferenças entre previsões geradas pelas duas visões, isto é, a frequentista versus a bayesiana.

O foco aqui é ser objetivo, apresentando brevemente os conceitos básicos, as vantagens e diferenças entre as abordagens, em uma tentativa bem humilde de fechar o gap entre as duas visões em termos introdutórios. Para mais detalhes e aprofundamento nos tópicos confira os cursos de Séries Temporais e Estatística Bayesiana.

ARIMA

Para não complicar, vamos considerar um modelo autoregressivo (AR) simples neste exercício. Como este modelo se parece?

y_t = c + ϕ₁y_t-1 + ϕ₂ y_t-2 + ⋯ + ϕ_py_t-p + ε_t

onde:

c → uma constante;

ϕ₁, ⋯, ϕ_p → parâmetros desconhecidos do modelo;

ε_t → termo de erro que segue uma distribuição normal, ε_t ∼ N(μ, σ²).

O modelo é autoregressivo pois, como pode ser observado, se trata de uma regressão da variável contra ela mesma (defasagens). Esse modelo é comumente denominado com o acrônimo AR(p), onde p é a ordem de defasagens da variável de interesse y_t e é um caso especial de um modelo ARIMA(p, 0, 0)¹.

Ok, mas visualmente, como um processo AR(p) se parece?

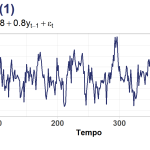
Podemos visualizar uma série temporal que segue um processo, por exemplo, de AR(1) com uma simulação simples (estou usando o R para isso), conforme abaixo:

Estimador MQO

Você deve ter notado que valores para a constante e para o primeiro parâmetro do AR(1), c = 18 e ϕ₁ = 0.8, "caíram do céu". Na vida real, fora da simulação, devemos estimar esses valores, eles são desconhecidos. Portanto, como os parâmetros do modelo são estimados?

Existem algumas maneiras de estimar os parâmetros do modelo, o padrão comum é através do estimador de mínimos quadrados ordinários (MQO), onde o objetivo é encontrar valores ótimos para os parâmetros c e ϕ_p do modelo minimizando a soma dos quadrados dos resíduos, sob diversas premissas. Ao usar essa abordagem, os parâmetros do modelo autoregressivo são fixos: cada observação t da série temporal y é associada com um mesmo valor estimado do parâmetro ϕ_p.

Isso é factível? E se você acredita que o valor ϕ_p não deveria ser fixo? Como poderíamos incorporar essa crença ao modelo? É aqui que entra a abordagem bayesiana! Mas antes, vamos dar uma olhada em dados reais para tentar entender a importância e uma motivação adjacente do assunto.

Exemplo: IPCA

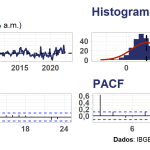
Como exemplo, abaixo apresento visualizações gráficas da série do IPCA sazonalmente ajustado, uma medida de inflação divulgada pelo IBGE, expresso em variação % ao mês.

Note que pela distribuição dos dados o IPCA apresenta uma média de aproximadamente 0,5% com uma cauda pesada à direita. Isso é característico do que chamam de outliers ou valores extremos e pode ser um problema em métodos econométricos. Além disso, a série apresenta uma autocorrelação significativa na primeira defasagem, o que pode ser um sinal para modelagem ARIMA, se supormos que tal classe de modelos univariados é suficiente em explicar a inflação.

Dada essa simples inspeção visual dos dados o que frequentistas e bayesianos poderiam tirar de conclusão? Um frequentista diria, dentre outras coisas, que a variância da série é a mesma para qualquer janela amostral, enquanto que um bayesiano diria que a variância pode variar.

Nessa mesma linha, um frequentista poderia estimar um modelo autoregressivo por MQO para explicar a inflação, mas ao fazê-lo estaria encontrando um valor fixo associado a defasagens da inflação, o que é equivalente a dizer que a maldita inércia inflacionária — um fenômeno econômico — não se alterou em todos esses mais de 20 anos de Plano Real. Isso é plausível? Certamente não é uma pergunta trivial de ser respondida, mas exercícios prévios do colega Vitor Wilher sugerem que a inércia inflacionária vem mudando recentemente.

Ou seja, são nesses pontos, para citar apenas alguns, que as abordagens divergem. Em outras palavras, frequentistas e bayesianos fazem diferentes suposições sobre os dados e sobre os parâmetros de um modelo em questão.

Portanto, voltando à questão, como a modelagem bayesiana incorpora sua visão sobre os parâmetros ao modelo?

A abordagem bayesiana

Na abordagem bayesiana, ao invés de tentarmos encontrar um valor ótimo para os parâmetros do modelo, nesse caso um AR(p), começaríamos por assumir um distribuição de probabilidade a priori para os mesmos e, então, usaríamos o teorema de Bayes. Ou seja, em nosso exemplo o que muda é que você assume uma distribuição a priori para os valores desconhecidos de c, ϕ₁,⋯ ,ϕ_p, σ², antes mesmo dos dados serem observados.

Mas de onde essa distribuição a priori vem? Bom, há muito o que se discutir sobre esse ponto, mas em resumo:

• Estudos prévios ou trabalhos publicados;
• Intuição do analista/pesquisador;
• Conhecimento da área/expertise;
• Conveniência;
• Métodos não paramétricos e outras fontes de dados.

Você pode pensar nessa distribuição a priori como uma crença/conhecimento prévio ou, no caso de você possuir estimativas prévias dos parâmetros do modelo, essas estimativas prévias se tornam a distribuição a priori.

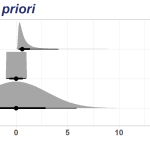
Voltando ao exemplo do IPCA, supondo que queiramos estimar um modelo AR(1), y_t = c + ϕ₁y_t-1 + ε_t, como definiríamos distribuições a priori para os parâmetros? Vamos começar admitindo que não sabemos muito sobre os parâmetros, apenas sabemos que para um AR(1) ser estacionário o parâmetro ϕ₁ precisar ser menor do que 1 em módulo², então vamos assumir distribuições genéricas:

Como é um primeiro modelo, vamos ser bem vagos sobre as escolhas. Partindo de um entendimento básico sobre o modelo, sabemos que o parâmetro |ϕ₁| < 1 para caracterizar um processo estacionário e que a variância dos erros deve ser positiva. Dessa forma utilizaremos, respectivamente, a distribuição uniforme e a gamma inversa e, quando não, a normal, assumindo os valores abaixo:

A interpretação destas distribuições a priori é de que não estamos informando em nosso modelo AR(1) bayesiano sobre quais poderiam ser os valores dos parâmetros. A estimativa final, pelo teorema de Bayes, dependerá dos dados observados e das priors assumidas. Vamos definir isso brevemente:

O que essa equação nos diz, em termos simples? A priori é a probabilidade de algo acontecer antes de incluirmos a probabilidade dos dados (verossimilhança), e a posteriori é a probabilidade após a incorporação dos dados. Ou seja, o teorema de Bayes nos fornece um método para atualizar nossa crença sobre parâmetros desconhecidos para cada informação nova (observações), condicionando a probabilidade aos dados observados.

Para estimar um modelo AR(p) na abordagem bayesiana será utilizado, geralmente, um método chamado Monte Carlo Markov Chain (MCMC). Apesar do nome apavorante, é um procedimento relativamente simples. O objetivo é "caminhar" aleatoriamente por um espaço de parâmetros para encontrar as estimativas e, assim, desenhar uma estimativa da posteriori, a nossa distribuição de principal interesse.

Comparação

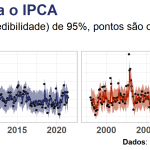
Agora vamos comparar as estimativas de um modelo AR(1) para o IPCA geradas pela visão frequentista vs. bayesiana³. Indo direto ao ponto, abaixo plotamos os resultados:

Aqui eu omito a distribuição a posteriori, que representaria a incerteza da estimativa bayesiana, exibindo apenas a a estimativa média dessa distribuição.

Note que as estimativas pontuais dentro da amostra são praticamente idênticas (eu separei em dois gráficos para melhor visualizar cada linha), refletindo semelhanças nos parâmetros estimados da abordagem bayesiana e da frequentista. O valor estimado para a constante é aproximadamente 0,20 e 0,19, respectivamente, enquanto que o ϕ₁ é 0,6 e 0,6. Por quê? A razão é decorrente do fato que a estimativa pontual do método frequentista, por MQO, é, em verdade, a mesma coisa que maximizar a probabilidade a posteriori de uma regressão linear bayesiana, que no caso representa a moda da distribuição.

Ok, mas comparamos somente estimativas pontuais um passo a frente dentro da amostra. O que acontece se compararmos ambas as abordagens em termos de previsão fora da amostra? No gráfico acima as últimas 12 observações do IPCA foram omitidas dos modelos, justamente para ter um período pseudo fora da amostra que nos permita gerar previsões e compará-las com os dados observados, podendo dessa forma avaliar a performance preditiva de cada modelo para dados que os mesmos ainda não conhecem.

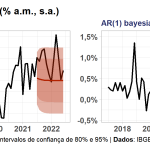
Gerando previsões pseudo fora da amostra 12 períodos (meses) a frente, temos os seguintes resultados:

Comentários

Apesar de ambas as previsões serem visivelmente ruins — acredito eu que não devido ao método de estimação em si, mas sim por conta da especificação/modelo simples para os dados e pela janela amostral (choques) "desfavorável" —, podemos notar uma grande diferença nas previsões pontuais e nos intervalos. A abordagem frequentista simplesmente previu o retorno a média da série (o que nesse caso é menos pior), enquanto que a abordagem bayesiana previu uma deflação (o que não é a realidade brasileira no momento).

Pela simplicidade da especificação do modelo AR em questão não podemos esperar bons resultados, por qualquer método de estimação considerado, e uma comparação mais exigente e justa implementaria a técnica de validação cruzada, o que eu não fiz neste exercício. Além disso, questões adjacentes como a inspeção dos resíduos e dos parâmetros são importantes para diagnosticar o modelo, as quais também deixamos de lado aqui.

Em suma, estimamos um modelo AR(1) para o IPCA por dois métodos diferentes que fundamentalmente fazem a mesma coisa: eles usam a defasagem da inflação para explicá-la. A primeira abordagem foi um modelo autoregressivo clássico, usando o método dos mínimos quadrados ordinários (MQO). O segundo foi um mesmo modelo autoregressivo, mas com estimação bayesiana, explorando a ideia de usar distribuições a priori para obter estimativas pontuais de distribuições a posteriori. Apesar disso, os resultados não foram satisfatórios. Ou seja, há trabalho ainda a se fazer, além de outros modelos a se testar.

Se o assunto te interessou e se você quiser saber mais sobre os temas abordados, dê uma olhada nos cursos de Séries Temporais e Estatística Bayesiana. Para ter acesso aos códigos deste exercício faça parte do Clube AM.

^1,2 Veja mais em Hyndman e Athanasopoulos (2021).

³ Aqui eu relaxei a restrição de distribuição uniforme para o parâmetro ϕ_1, por recomendação dos desenvolvedores do pacote utilizado e por falha de inicialização da estimação. A priori desse parâmetro passou então para ϕ₁ ∼ Normal(0, 0.5).

Referências

Box, G. E. P., & Jenkins, G. M. (1970). Time series analysis: Forecasting and control. Holden-Day.

Durbin, J., & Koopman, S. J. (2012). Time series analysis by state space methods (Vol. 38). OUP Oxford.

Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2022-07-20.